散布矩阵(scatter_matrix)及相关系数(correlation coefficients)实例分析

article/2025/10/29 15:40:07

在进行机器学习建模之前，需要对数据进行分析，判断各特征(属性，维度)的数据分布及其之间的关系成为十分必要的环节，本文利用Pandas和Numpy的散布矩阵函数及相关系数函数对数据集特征及其关系进行实例分析。

散布矩阵(scatter_matrix)

Pandas中散布矩阵的函数原型为：

def scatter_matrix(frame, alpha=0.5, figsize=None, ax=None, diagonal='hist', marker='.', density_kwds=None,hist_kwds=None, range_padding=0.05, **kwds)

各参数如下：

  • frame：(DataFrame)，DataFrame对象
  • alpha：(float, 可选)， 图像透明度，一般取(0,1]
  • figsize: ((float,float), 可选)，以英寸为单位的图像大小，一般以元组 (width, height) 形式设置
  • ax：(Matplotlib axis object, 可选)，一般取None
  • diagonal：({‘hist’, ‘kde’})，必须且只能在{‘hist’, ‘kde’}中选择1个，’hist’表示直方图(Histogram plot),’kde’表示核密度估计(Kernel Density Estimation)；该参数是scatter_matrix函数的关键参数，下文将做进一步介绍
  • marker：(str, 可选)， Matplotlib可用的标记类型，如’.’，’,’，’o’等
  • density_kwds：(other plotting keyword arguments，可选)，与kde相关的字典参数
  • hist_kwds：(other plotting keyword arguments，可选)，与hist相关的字典参数
  • range_padding：(float, 可选)，图像在x轴、y轴原点附近的留白(padding)，该值越大，留白距离越大，图像远离坐标原点
  • kwds：(other plotting keyword arguments，可选)，与scatter_matrix函数本身相关的字典参数

‘hist’值

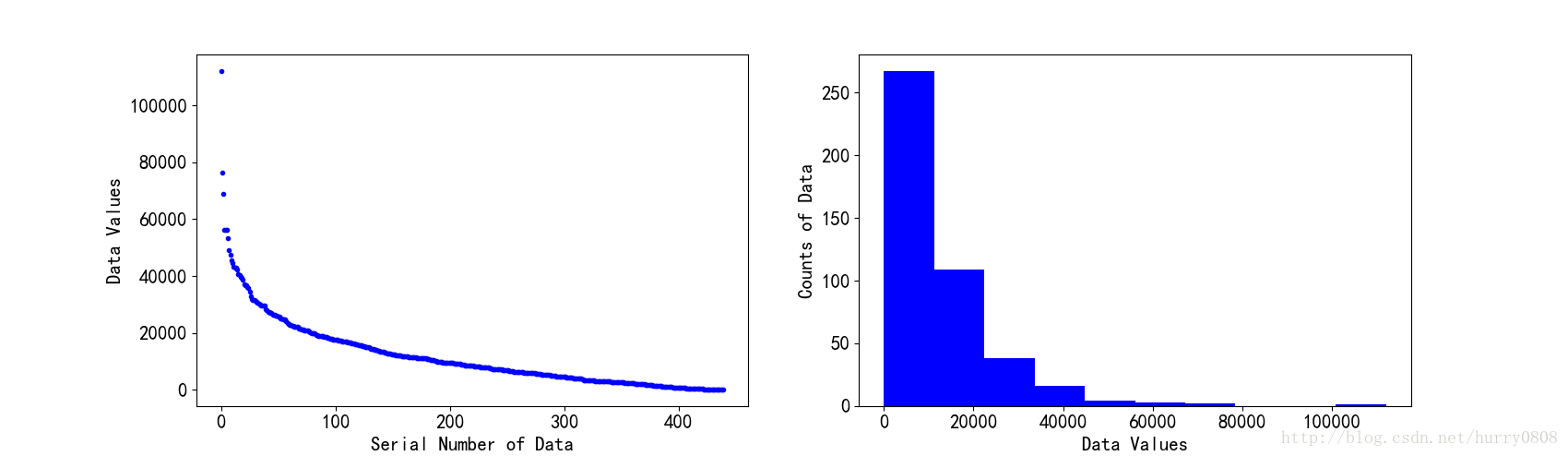
diagonal参数取’hist’值时，表示散布矩阵的对角线上的图形为数据集各特征的直方图。直方图是一种可对值频率进行离散化显示的柱状图，数据点被拆分到离散的，间隔均匀的面元中，绘制的是各面元中数据点的数量。
例如有1维整型数组，共有元素440个，按照值从大至小的顺序排列后，其散布图与直方图如下所示：
这里写图片描述

‘kde’值

diagonal参数取’kde’值时，表示散布矩阵的对角线上的图形为数据集各特征的核密度估计(Kernel Density Estimation，KDE)。核密度估计是在概率论中用来估计未知的密度函数，属于非参数检验方法之一。简单来说，核密度估计就是在当前数据集(连续型数据样本)已知的情况下，通过计算来获取该样本分布的概率密度函数；在计算获取时需要用到核函数，如Gaussian Kernel Density、Exponential Kernel Density、Cosine Kernel Density等，不同核函数可以得到样本整体趋势和密度分布规律性基本一致的结果；影响该结果的还包括带宽（bandwidth），带宽值过大或过小都会影响估计结果；关于核密度估计的进一步论述请参考这里。
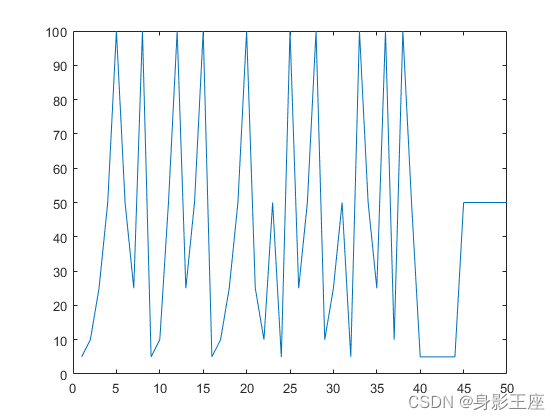
以相同的1维整型数组为例，使用Gaussian Kernel Density估计得到的密度函数如下所示：
这里写图片描述

scatter_matrix函数实例

以优达学城的数据集为例，来说明散布矩阵函数的使用方法。该数据集是某供货商统计的各类客户的年度采购额，每行数据为1个客户的采购记录，共440行；数据集包括6个维度——Fresh(生鲜)、Milk(奶制品)、Grocery(杂货)、Frozen(冷藏食品)、Detergents_Paper(清洁纸)、Delicatessen(熟食品)，记录了客户采购不同门类产品的情况；数据集元素均为整型数据，无缺失值。

import pandas as pd
import matplotlib.pyplot as plt
try:data = pd.read_csv("customers_dataset.csv")
except:print "Dataset could not be loaded."
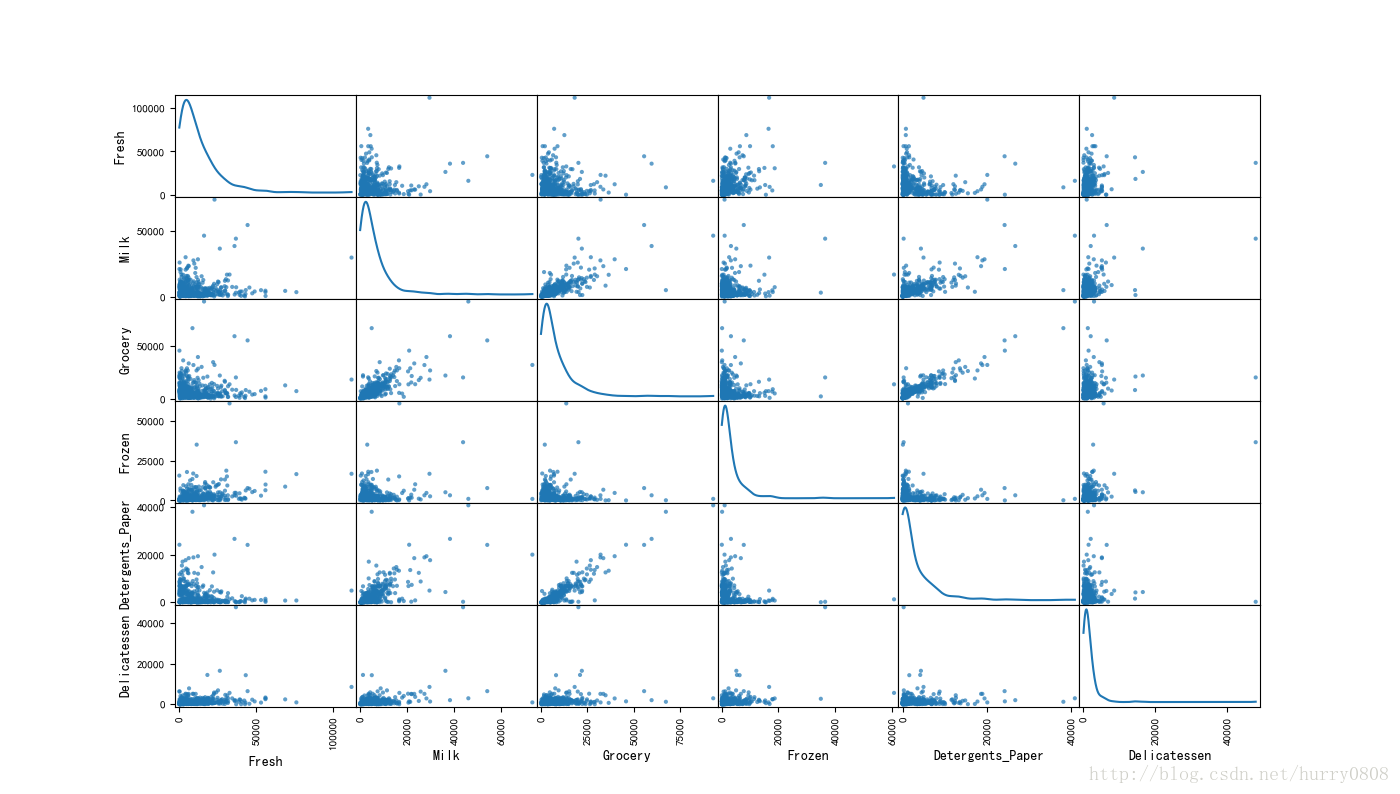
pd.plotting.scatter_matrix(data, alpha=0.7, figsize=(14,8), diagonal='kde')
plt.show()

这里写图片描述

在上文介绍diagonal参数取’hist’、’kde’值时，绘图所用数据为Fresh列数据；从图中可以看出，单列数据绘制的密度函数曲线与本图左上角第1个子图一致。
图中对角线上的子图均为经高斯核密度估计后的密度函数曲线，scatter_matrix函数源码中对应部分如下：

……
# Deal with the diagonal by drawing a histogram there.
if diagonal == 'hist':ax.hist(values, **hist_kwds)
elif diagonal in ('kde', 'density'):from scipy.stats import gaussian_kdey = valuesgkde = gaussian_kde(y)ind = np.linspace(y.min(), y.max(), 1000)ax.plot(ind, gkde.evaluate(ind), **density_kwds)
……

散布矩阵图呈对称结构，除对角上的密度函数图之外，其他子图分别显示了不同特征列之间的关联关系，如Grocery与Detergents_Paper之间、Grocery与Milk之间、Milk与Detergents_Paper之间近似成线性关系，说明该些特征之间关联性很强；相反地，其他各特征列之间的散布状态比较杂乱，基本无规律可循，说明各特征之间的关联性不强。
分析数据集各特征(列)之间的关系时，散布矩阵能以图形的形式“定性”给出各特征之间的关系，如要进一步“定量”分析，则需要使用相关系数。

相关系数(correlation coefficients)

在统计学中，皮尔逊积矩相关系数（Pearson product-moment correlation coefficient，又称作 PPMCC或PCCs, 常用r或Pearson’s r表示）用于度量两个变量X和Y之间的相关关系（线性相关），其值介于-1与1之间。在进行数据分析时，常用作度量各特征之间的相关程度。
Numpy中的计算相关系数的函数为：

corrcoef(x, y=None, rowvar=True, bias=<class numpy._globals._NoValue>, ddof=<class numpy._globals._NoValue>)

各参数如下：

  • x：(array_like)，包含多个特征和值的1维或2维数组，每行表示一个特征，每列表示各特征的取值，以行为依据计算各特征之间的相关系数
  • y：(array_like，可选)，一组额外的特征和值，数组形状与x相同
  • rowvar：(bool, 可选)，该值为True时，每行表示1个特征，各列表式各特征的取值；该值为False时，每列表示1个特征，各行表式各特征的取值；默认情况下为True
  • bias：(_NoValue，可选)，无效果，从1.10.0版本后废止
  • ddof ：(_NoValue，可选)，无效果，从1.10.0版本后废止

corrcoef函数实例

仍以优达学城的数据集为例，计算各特征之间的相关系数并绘图：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
try:data = pd.read_csv("customers_dataset.csv")
except:print "Dataset could not be loaded."
cov = np.corrcoef(data.T)
img = plt.matshow(cov,cmap=plt.cm.winter)
plt.colorbar(img, ticks=[-1,0,1])
plt.xticks(np.arange(len(data.keys())), data.keys())
plt.yticks(np.arange(len(data.keys())), data.keys())
plt.show()

这里写图片描述

该图形也为对称结构，依据相关系数的计算式，其对角线上的相关系数为1；子图颜色越接近绿色表示相关系数越接近1，特征相关性越强且为正相关，子图颜色接近另一个极端(-1)时，特征之间相关性也很强且为负相关；本例相关系数最小值为-0.132，蓝色最浓的子图即为该值，0处的颜色表示特征之间不相关(相关系数为0)。
从图中可以看出，Grocery与Detergents_Paper特征相关性最强，Grocery与Milk、Milk与Detergents_Paper特征之间也有较强相关性，其余各特征之间相关性较弱、甚至不相关，该结论与散布矩阵图得出的结论一致。

总结

对于给定数据集，Pandas的scatter_matrix函数能够显示各特征的密度函数曲线，能大致显示各特征之间的相关关系，Numpy的corrcoef函数能够准确计算各特征之间的相关系数，且能借助Matplotlib库以图形形式直观表达。

参考

http://blog.csdn.net/sinat_25059791/article/details/71336557


http://chatgpt.dhexx.cn/article/p7O2tc0j.shtml

相关文章

Probability And Statistics——CorrelationsCovariance

Probability And Statistics——CorrelationsCovariance

Skew&#xff08;偏度&#xff09; 在概率论和统计学中&#xff0c;偏度衡量实数随机变量概率分布的不对称性。偏度的值可以为正&#xff0c;可以为负或者甚至是无法定义。在数量上&#xff0c;偏度为负&#xff08;负偏态&#xff09;就意味着在概率密度函数左侧的尾部比右侧的…
阅读更多...
structural covariance network

structural covariance network

structural covariance network 结构协方差网络 结构协方差网络是一个较老的概念&#xff0c;只是近年受到了一定的重视。 大佬 Aaron Alexander-Bloch 在2013年通过一篇综述描述了这种结构协方差网络的应用意义及前景。 既往一般是在bold信号和fiber tracking建立连接&#xf…
阅读更多...
_variant_t、CComVariant与COleVariant、CDBVariant

_variant_t、CComVariant与COleVariant、CDBVariant

目前计算机语言多种多样&#xff0c;如C、Java、Basic、Pascal等&#xff0c;此外还有JavaScript、VBScript、ActionScript等脚本语言&#xff0c;它们各自维护自己的数据类型&#xff0c;当使用C这样强类型的语言来读取数据库或者与其他语言之间来交换数据时&#xff0c;它很有…
阅读更多...
Partial correlation coefficient

Partial correlation coefficient

利用PYTHON计算偏相关系数&#xff08;Partial correlation coefficient) 在统计学中&#xff0c;我们经常使用皮尔逊相关系数来衡量两个变量之间的线性关系。然而&#xff0c;有时我们感兴趣的是理解两个变量之间的关系&#xff0c;同时控制第三个变量。 例如&#xff0c;假设…
阅读更多...
Multilevel Cooperative Coevolution for Large Scale Optimization

Multilevel Cooperative Coevolution for Large Scale Optimization

0、论文背景 本文在CCEA_G的基础上&#xff0c;提出了MLCC框架。在MLCC中&#xff0c;基于不同组大小的随机分组策略构造了一组问题分解器。演化过程分为若干个循环&#xff0c;在每个周期开始时&#xff0c;MLCC使用自适应机制根据其历史性能选择分解器。由于不同的组大小捕获…
阅读更多...
mean value coordinates(均值重心坐标)定义及证明

mean value coordinates(均值重心坐标)定义及证明

欢迎关注更多精彩 关注我&#xff0c;学习常用算法与数据结构&#xff0c;一题多解&#xff0c;降维打击。 在图形学中对于物体的描述往往是离散&#xff0c;但是在具体展示过程中我们又希望是连续。线性插值是解决离散与连续的常用手段。 三角形中的插值点击前往凸四边形中的…
阅读更多...
numpy中的convolve的理解

numpy中的convolve的理解

写在前面 浏览更多内容&#xff0c;可访问&#xff1a;http://www.growai.cn 欢迎您关注作者知乎&#xff1a;ML与DL成长之路 推荐关注公众号&#xff1a;AI成长社&#xff0c;ML与DL的成长圣地。 函数 numpy.convolve(a, v, mode‘full’)&#xff0c;这是numpy函数中的卷…
阅读更多...
Clustering Coefficient

Clustering Coefficient

Define Clustering Coefficient&#xff1a;聚类系数 Clustering Coefficient measures the degree to which nodes in a network tend to cluster or form triangles. ——聚类系数衡量网络中节点倾向于聚类或形成三角形的程度 Triadic Closure 三元闭包 The tendency of…
阅读更多...
covariate(covariate是控制变量吗)

covariate(covariate是控制变量吗)

如何用STATA对连续性变量进行meta回归分析 在stata中有个metareg命令&#xff0c;好像可以对连续变量进行回归分析。 附件中是一篇pdf文档&#xff0c;主要介绍stata中关于meta分析的命令。跟大家分享一下。 里面在提到metareg命令时&#xff0c;列举了以下三个列子&#xff1a…
阅读更多...
协方差矩阵简介（Covariance Matrix）

协方差矩阵简介（Covariance Matrix）

协方差矩阵定义 首先我们要明白&#xff0c;协方差实际是在概率论和统计学中用于衡量两个变量的总体误差,当然方差是协方差的一种特殊情况&#xff0c;即当两个变量是相同情况。它表示的是两个变量的总体的误差&#xff0c;这与只表示一个变量误差的方差不同。如果两个变量的变…
阅读更多...
covariance matrix

covariance matrix

协方差的定义 对于一般的分布&#xff0c;直接代入E(X)之类的就可以计算出来了&#xff0c;但真给你一个具体数值的分布&#xff0c;要计算协方差矩阵&#xff0c;根据这个公式来计算&#xff0c;还真不容易反应过来。这里用一个例子说明协方差矩阵是怎么计算出来的吧。 记住&…
阅读更多...
经典排序算法——堆排序

经典排序算法——堆排序

对于一个int数组&#xff0c;请编写一个堆排序算法&#xff0c;对数组元素排序。 给定一个int数组A及数组的大小n&#xff0c;请返回排序后的数组。 测试样例&#xff1a; [1,2,3,5,2,3],6 [1,2,2,3,3,5] class HeapSort { public:int* heapSort(int* A, int n) {BuildMaxHeap(…
阅读更多...
堆排序算法原理及c++实现

堆排序算法原理及c++实现

文章目录 准备知识MAX-HEAPIFY过程建堆堆排序算法总结 准备知识 堆的结构可以分为最大堆和最小堆&#xff0c;是一个完全二叉树&#xff0c;而堆排序是根据堆的这种数据结构设计的一种排序。 所谓完全二叉树即叶节点只能出现在最下层和次下层&#xff0c;并且最下面一层的结点…
阅读更多...
堆排序算法设计与分析

堆排序算法设计与分析

堆排序(HeapSort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法&#xff0c;它是选择排序的一种。堆分为大根堆和小根堆&#xff0c;是完全二叉树。大根堆要求父结点的值大于或等于子结点的值&#xff0c;小根堆相反。根据大根堆的性质&#xff0c;我们可以知道最大值一…
阅读更多...
堆排序算法实现

堆排序算法实现

堆排序:结构逻辑上是完全二叉树,但是可以使用顺序存储来实现 一些二叉树的区别: 二叉树:度数最大为2并且每个子树也是二叉树 满二叉树:每层节点都是满的,没有空缺,也就是,叶子节点只能出现在最后一层 完全二叉树:限制条件比满二叉树弱化,只需要前k-1层是满二叉树结构,最后…
阅读更多...
数据结构之堆排序算法详解+C语言实现

数据结构之堆排序算法详解+C语言实现

堆 　　堆是具有以下性质的完全二叉树&#xff1a;每个结点的值都大于或等于其左右孩子结点的值&#xff0c;称为大顶堆&#xff1b;或者每个结点的值都小于或等于其左右孩子结点的值&#xff0c;称为小顶堆。 堆排序 　　堆排序是利用堆这种数据结构而设计的一种排序算法&…
阅读更多...
堆排序算法原理及实现

堆排序算法原理及实现

堆排序是排序中一种比较重要的算法&#xff0c;和快速排序一样&#xff0c;其复杂度也是O(nlogn)&#xff1b;同时也是一种原地排序算法&#xff1a;在任何时候&#xff0c;数组中只有常数个元素存储在输入数组以外。堆这种数据结构是处理海量数据比较常见的结构&#xff0c;海…
阅读更多...
堆排序算法Java

堆排序算法Java

基本原理 1):将带排序的序列构造成一个大顶堆&#xff0c;根据大顶堆的性质&#xff0c;当前堆的根节点&#xff08;堆顶&#xff09;就是序列中最大的元素 2):将堆顶元素和最后一个元素交换&#xff0c;然后将剩下的节点重新构造成一个大顶堆&#xff1b; 3):重复步骤2 小知识…
阅读更多...
堆排序算法详细分析

堆排序算法详细分析

一、堆相关概念 1.堆 堆是完全二叉树&#xff0c;即除最后一层外&#xff0c;其它层都是满的&#xff0c;且最后一层从左到右依次都有元素。如下图所示。 堆是用数组来实现的&#xff0c;图中下标就为数组的下标&#xff0c;其对应数组[5, 1, 7, 2, 8, 6, 3, 9, 4]&#xf…
阅读更多...
数据结构——堆排序（算法）

数据结构——堆排序（算法）

基本介绍 1&#xff09;、堆排序是利用堆这种数据结构而设计的一种排序算法&#xff0c;堆排序是一种选择排序&#xff0c;它的最好、最坏、平均时间复杂度均为O(nlogn)&#xff0c;它也是不稳定排序。2&#xff09;、堆是具有以下性质的完全二叉树&#xff1a;每个节点的值都…
阅读更多...
推荐文章

Copyright @ 2022~2023