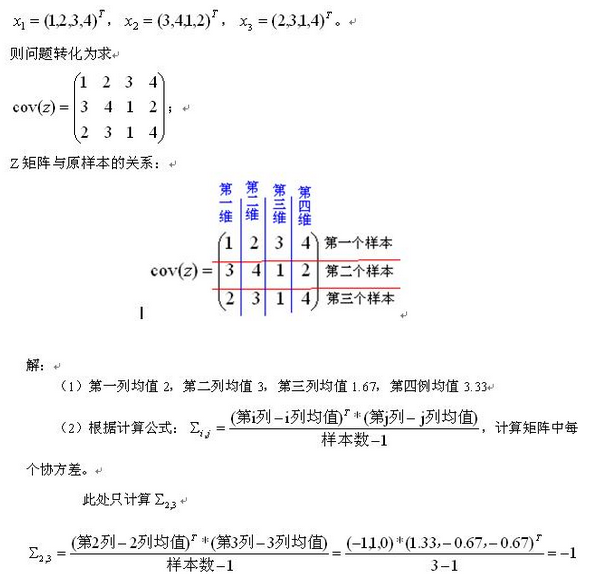
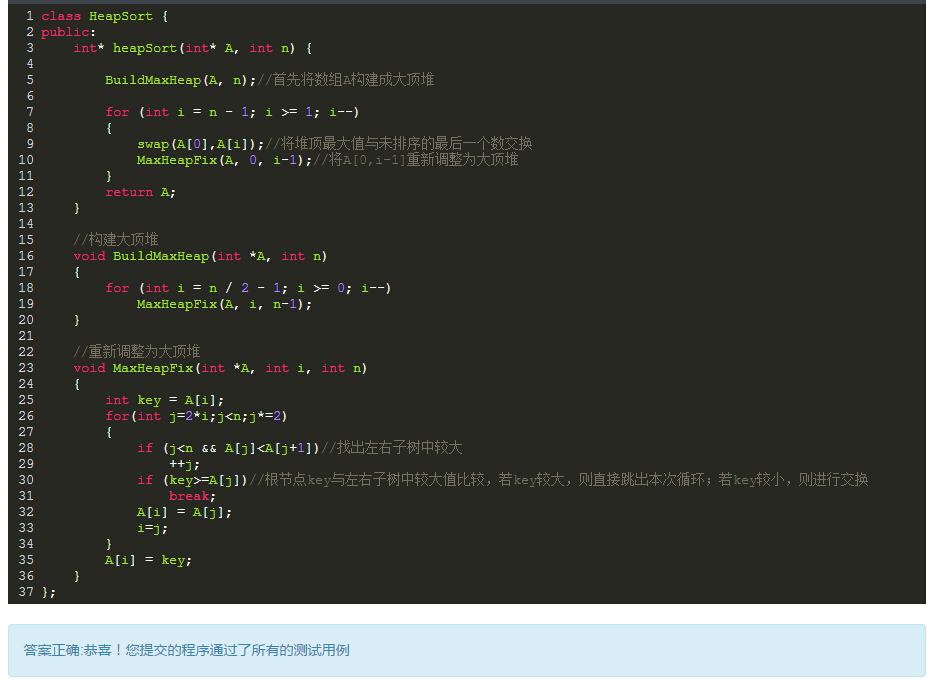
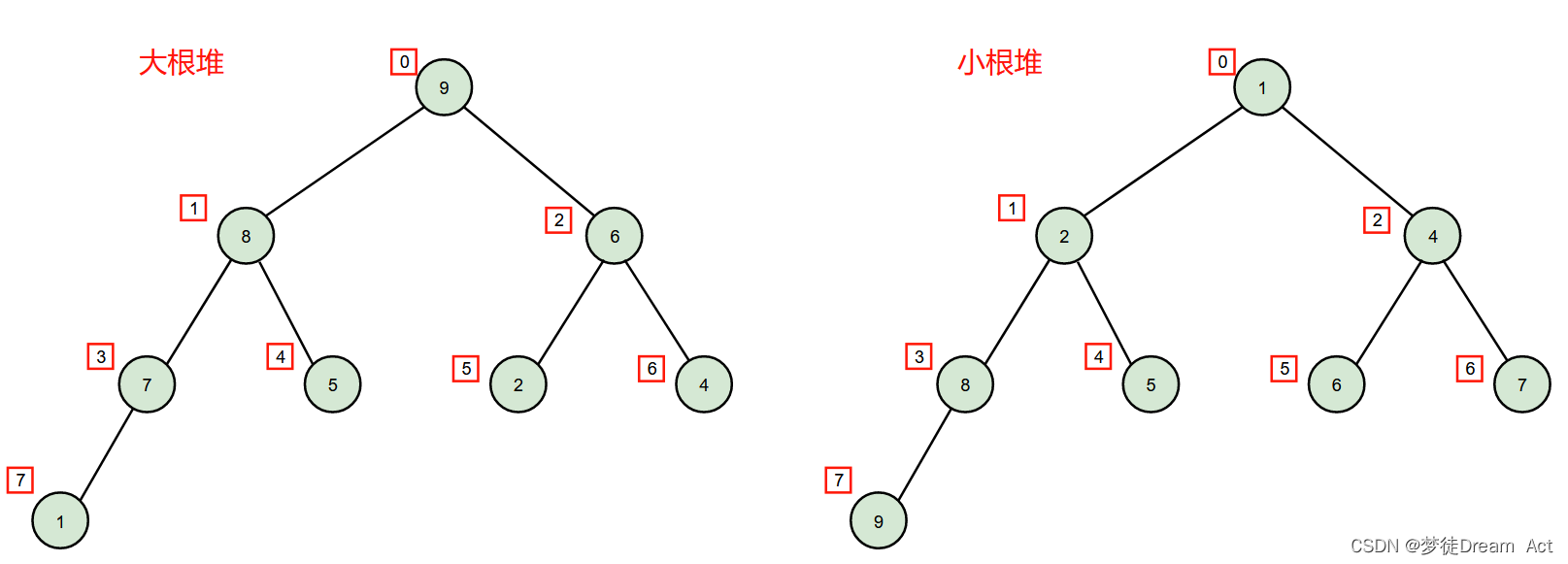
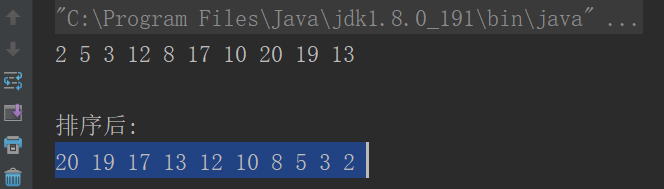
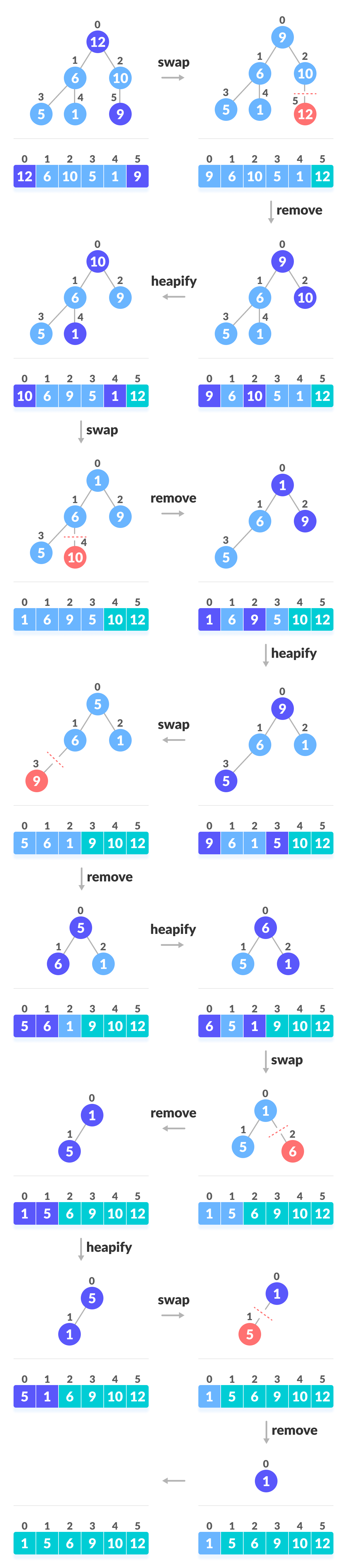
0、论文背景
本文在CCEA_G的基础上,提出了MLCC框架。在MLCC中,基于不同组大小的随机分组策略构造了一组问题分解器。演化过程分为若干个循环,在每个周期开始时,MLCC使用自适应机制根据其历史性能选择分解器。由于不同的组大小捕获了原始目标变量之间的不同交互水平,MLCC能够在不同水平之间自我适应。
Yang Z, Tang K, Yao X. Multilevel cooperative coevolution for large scale optimization[C]//2008 IEEE congress on evolutionary computation (IEEE World Congress on Computational Intelligence). IEEE, 2008: 1663-1670.
1、MLCC
本文是在CCEA_G的基础上,提出了MLCC,CCEA_G请参照博客:CCEA_G。
在有关子空间大小的讨论中,在早期阶段,维度小的子空间有助于快速找到好的区域;但在后期阶段,大的子空间有助于子问题包含更多的全局信息,这对于微调很重要。如果算法能够根据目标函数、演化阶段和特征特征适应适当的群大小,将是理想的。
在MLCC中,我们首先设计了基于不同组大小的几个问题分解器来形成一个分解器池。池中的每个分解器都意味着目标变量之间的不同交互水平。演化过程分为几个循环。在每个周期开始时,MLCC根据它们的性能记录从分解器池中选择一个分解器。然后,MLCC使用所选的分解器将目标向量问题划分为几个子分量,并对每个子分量用一定的EA进行演化。在每个周期结束时,所选分解器的性能记录将随其在当前周期中的性能而更新。
MLCC的算法流程如下:
- 设置分解器池,
。
表示子种群维度。
- 初始化分解器的性能记录表,
,
对应
。
- 种群的初始化,
,NP表示种群数,n表示变量维度。
- 求取种群对应的适应度函数值,设置最优值为v。
,达到本次程序执行终止条件,返回步骤2。
- 计算分解器池中每个分解器的选择概率:
- 根据p从S中选择
,选取p中最大值对应的s。
- 将n维向量划分为
组,
。
- 设置 c = 1。
- 获得种群的子种群,
。
- 使用EA优化子种群。
- 如果 c < m,c++,并返回步骤10。
- 评估优化后的种群的适应度值,获得当前最佳值v`。
- 更新
,并使 v = v`。
- 如果满足停止条件,则停止;否则,下一个循环将进入步骤6。
2、算法的实现和简单验证
CCEA_G在上面提到的博客中有实现,MLCC的实现如下:
clc;clear;clearvars;
addpath('CEC2008\');
global initial_flagNS = 100; % 种群数
dim = 500; % 种群维度
upper_bound = [100,100,100,5,600,32,1]; % 搜索区间:f1[-100,100],f2[-100, 100],f3[-100,100],f4[-5,5],f5[-600,600],f6[-32,32],f7[-1,1]
lower_bound = [-100,-100,-100,-5,-600,-32,-1];
bestYhistory = []; %保存每次迭代的最佳值
sList = [5,10,25,50,100]; %组大小池
sHistory = [];
r = ones(1,5);for func_num = 3initial_flag = 0; % 换一个函数initial_flag重置为0sample_x = lhsdesign(NS, dim).*(upper_bound(func_num) - lower_bound(func_num)) + lower_bound(func_num).*ones(NS, dim); % 生成NS个种群,并获得其评估值sample_y = benchmark_func(sample_x,func_num);[best_y, bestIndex] = min(sample_y); %获取全局最小值以及对应的种群best_x = sample_x(bestIndex,:);v1 = best_y;for i0 = 1 : 50 %迭代50次p = exp(r .* 7);p = p ./ sum(p);[~, index2] = max(p); % 获取最大p值对应的索引s = sList(1,index2); % 子空间的数目sHistory = [sHistory;s];index = randperm(dim); %随机划分子空间for i1 = 1 : sindex1 = index(((i1 - 1) * (dim / s) + 1) : (i1 * (dim / s)));sub_x = sample_x(:,index1);sub_x = SaNSDE(sub_x, sample_y, best_x, index1, 70, dim / s, lower_bound(func_num), upper_bound(func_num), @(x)benchmark_func(x,func_num));%100*70sample_x(:,index1) = sub_x;sample_y = benchmark_func(sample_x,func_num); %100[~, bestIndex] = min(sample_y); %获取全局最小值以及对应的种群best_x = sample_x(bestIndex,:);end[worse_y, worseIndex] = max(sample_y); %获取全局最大值以及对应的种群randIndex = randi(NS);while randIndex == bestIndex || randIndex == worseIndexrandIndex = randi(NS); % 随机获取一个值end[sample_x(worseIndex,:),sample_y(worseIndex,:)] = NSDE(sample_x(worseIndex,:), NS, 50, s, -2, 2, 0.9, @(x)benchmark_func(x,func_num));% 50*100[sample_x(bestIndex,:),sample_y(bestIndex,:)] = NSDE(sample_x(bestIndex,:), NS, 50, s, -2, 2, 0.9, @(x)benchmark_func(x,func_num));% 权重向量在[-2,2]之间搜寻[sample_x(randIndex,:),sample_y(randIndex,:)] = NSDE(sample_x(randIndex,:), NS, 50, s, -2, 2, 0.9, @(x)benchmark_func(x,func_num));[best_y, bestIndex] = min(sample_y); %获取全局最小值以及对应的种群best_x = sample_x(bestIndex,:);bestYhistory = [bestYhistory;best_y];v2 = best_y;r(1,index2) = (v1 - v2) / abs(v1); %更新r向量v1 = v2;end
end
figure(1);
plot(bestYhistory);
figure(2);
plot(sHistory);f3函数CCEA_G的优化效果:
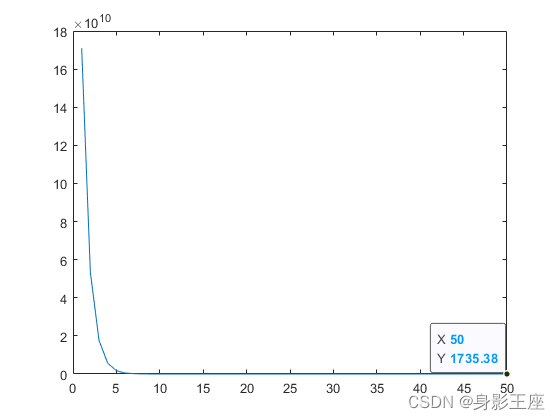
f3函数MLCC的优化效果:
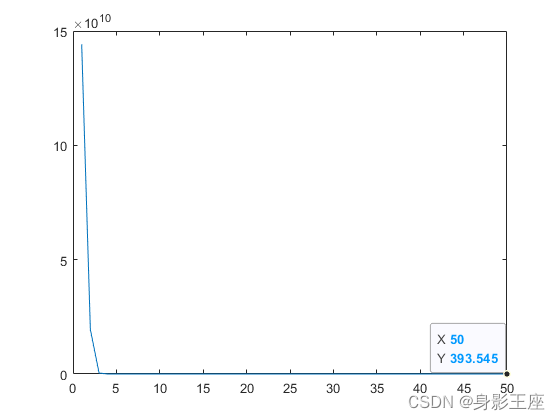
f3函数MLCC的子种群个数选择图:
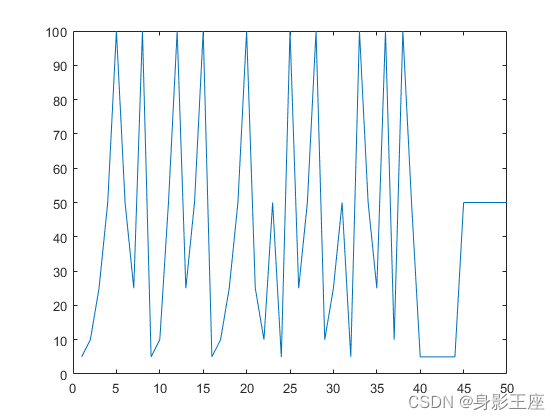
由此可见,动态确定分组大小,确实要好一些。
如有错误,还望批评改正!