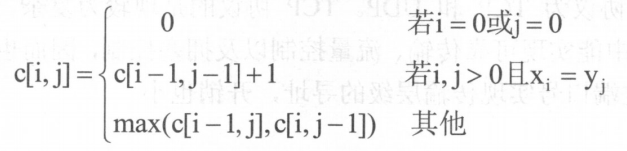先搞明白R树搜索、插入、删除过程。
R树是平衡树,可以理解为B树在N维空间上的扩展。
R树一定要满足一下要求:
1.根节点若非叶子节点,则至少有两个子节点;
2.每个非根叶节点和非叶节点包含的实体个数均介于m和M之间;
3.所有叶子节点在同一层次;
其中m表示拥有子节点的下限,目的是为了提高磁盘利用率,提高搜索效率。如果m=1,所有节点都只有一个子节点,那树就退化为了普通链表。当节点的子节点数量少于m时,则会删除该节点,把该节点的子节点分配到其他节点中;M表示拥有子节点的上限,因为一般情况下,出于减少磁盘IO和批量刷盘的目的,我们一个节点对应了磁盘中一个或若干页。当节点的子节点数量大于M时,则会分裂该节点,把子节点分配到两个新的节点中。一般情况下m=1/2M。
我们就用二维空间来举例说明。
比如有如下二维平面坐标内若干点:

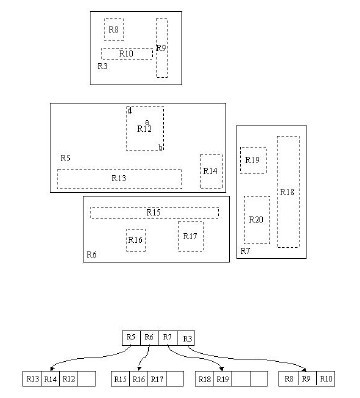
我们会把相邻的点分组聚集到一起,并用外接矩形框住,如下图:

这样我们就认为A、B、C的父节点是R1;H、G、P的父节点是R2。以此反复,R1、R2、R3、R4、R5、R6再把相邻的聚集到一起,用外接矩形框柱,外接矩形为其父节点。直到剩下两个节点为止。那最终R树的形态如下图:


RR2子节点就不详细画了。可以看到这就组成了一棵R树。
那搜索过程是什么样的?
比如我们认为这些点都是饭店坐标,我们要查一下我附近一公里范围内的所有饭店,那就把我附近一公里的范围作为一个查询矩形,然后从根节点开始,搜索所有相交的矩形。步骤如下:
S1:[查找子树]如果T是非叶子结点,如果T所对应的矩形与S有重合,那么检查所有T中存储的条目,对于所有这些条目,使用Search操作作用在每一个条目所指向的子树的根结点上(即T结点的孩子结点)。
S2:[查找叶子结点]如果T是叶子结点,如果T所对应的矩形与S有重合,那么直接检查S所指向的所有记录条目。返回符合条件的记录。

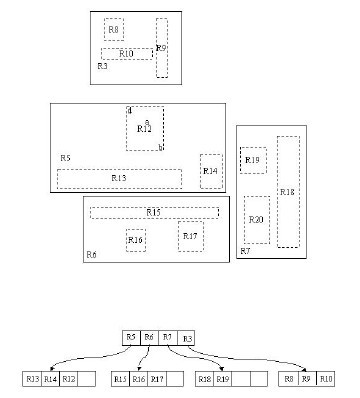
比如图中,黑色矩形为我们的搜索矩形,从根节点开始,搜索矩形与RR1、RR2都相交,则分别再搜索他们的子节点。RR1的子节点R1、R6与搜索矩形相交,RR2的子节点R2与搜索矩形相交。
然后再搜索R1、R6、R2的子节点是否符合条件。可以看到C、L、K、J、G在搜索矩形内,所以返回结果为C、L、K、J、G这五个节点。
再看插入过程,插入过程比较复杂一点,但是记住几个关键点即可:
1.如何找到合适的节点插入
2.如果节点的子节点数量超过M,怎么办
3.如果分裂向上传递怎么办
合适节点的选择要保证一个规则即可:加入的新节点使得矩形扩张最小,如果扩张相同,则选择面积小的。
如果插入新子节点导致子节点的数量超过M,则对节点进行分裂,分裂后的两个新结点,要包含原来所有的子节点。
如果分裂上传,则重复分裂过程,直到上传到根节点。
我们举例说明一下,我们假设M=4,m=2:

我们新增了红色节点,从根节点开始搜索合适的插入节点。红色节点与RR1近(即RR1扩张小),则选择RR1节点。
再搜索RR1子节点中,R6加入新节点后扩张小,则选择R6作为插入节点。
R6中已经有个4个子节点,再插入红色节点后,子节点数量大于M,则R6进行分裂。分裂产生R6和R7,并且R6、R7要包含原来所有的子节点。分裂后RR1的子节点数量为4,不需要再次分裂,则插入结束。插入后R树变为:

我们看一下分裂上传的场景,假如我们插入了很多节点后,R树已经变为如下图:

如果此时再向R1添加一个新节点,会导致R1分裂为两个节点,RR1的子节点也超过了上限M,则RR1也需要分裂,分裂为RR1和RR5,此时根节点的节点数量也超过了上限M,则重新创建根节点RRR1和RRR2,子节点分别为RR1、RR2、RR3、RR4、RR5,即树增高一层。
再看删除操作,删除操作也是需要注意几个关键点即可:
1.搜索到待删除的节点
2.如果删除后,节点的子节点数量小于m,则删除该节点
3.删除该节点后,需要把节点重新插入R树
如果节点的节点数量小于m,则把节点的子节点加入到临时链表中,一直到根节点为止。如果节点没有被删除,则调整矩形,使其可以覆盖所有子节点。如果临时链表中的节点需要插入回原来的层。
举例说明:

比如我们把A、C、D、I都删了,此时R1的子节点只剩下一个了,则B、E加入到临时链表中。
又因为R1、R3的子节点都剩下1个,小于m,则R1、R3被删除。
又因为此时RR1只剩下一个子节点R6,则把RR1的子节点添加到临时链表中。
此时遍历到根节点,则把临时链表中的数据重新插入会原层。
R6直接插入回RR1子节点,当插入B时,R6子节点数量已满,则R6分裂为R6和R7。
当插入E时,R6、R7子节点还有空余,则把B插入到R6或者R7中。
则删除后,R树变为:

以上是R树的操作过程。其中还有几个问题点:
1.相邻的节点或矩形,是如何划分的。
2.矩形分裂后,是以什么规则划分新矩形的。
3.如果有一个节点与其他任何节点都不相邻,形成孤点,如何处理。
还需要再深入学习一下。
首发公众号: