【动态规划法】求解TSP问题

article/2025/9/29 19:59:48

问题详情

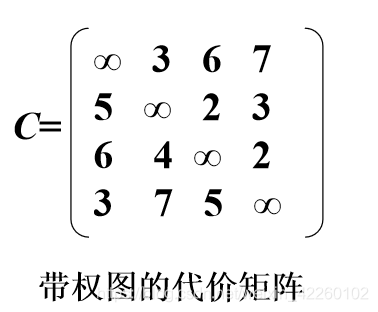
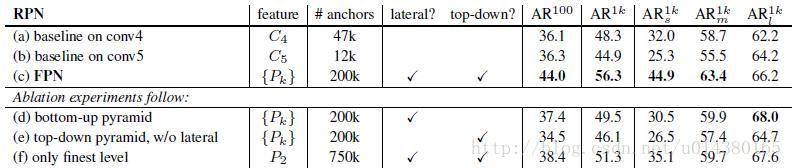
求解下图所示的TSP问题，计算出所经过的城市编号以及最短路径值，城市代价矩阵如图所示：

求解思路

假设从顶点i出发，令d(i, V’ )表示从顶点i出发经过V’ 中各个顶点一次且仅一次，最后回到出发点（i）的最短路径长度，开始时， V’ ＝V－{i}，于是，TSP问题的动态规划函数为：
d(i, V’ )=min{cik+d(k, V’ －{k})} (k∈V’)
d(k,{})=cki (k≠i) (从k出发到达i的距离)

计算过程

从0城市出发经城市1、2、3然后回到0城市的最短路径长度是：
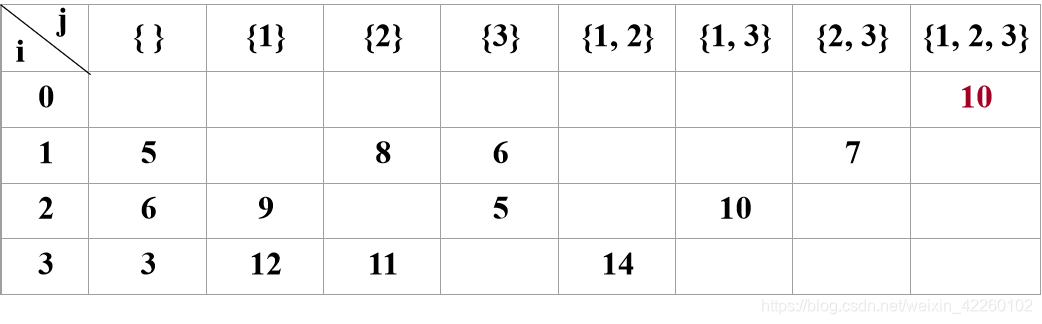
d(0,{1, 2, 3})=min{c01+d(1, { 2, 3}), c02+d(2, {1, 3}), c03+d(3, {1, 2})}
这是最后一个阶段的决策，而：
d(1, {2, 3})=min{c12+d(2, {3}), c13+ d(3, {2})}
d(2, {1, 3})=min{c21+d(1, {3}), c23+ d(3, {1})}
d(3, {1, 2})=min{c31+d(1, {2}), c32+ d(2, {1})}
这一阶段的决策又依赖于下面的计算结果：
d(1, {2})= c12+d(2, {}) d(2, {3})=c23+d(3, {})
d(3, {2})= c32+d(2, {}) d(1, {3})= c13+d(3, {})
d(2, {1})=c21+d(1, {}) d(3, {1})=c31+d(1, {})
而下式可以直接获得（括号中是该决策引起的状态转移）：
d(1, {})=c10=5(1→0) d(2, {})=c20=6(2→0) d(3, {})=c30=3(3→0)

再向前倒推，有：
d(1, {2})= c12+d(2, {})=2+6=8(1→2) d(1, {3})= c13+d(3, {})=3+3=6(1→3)
d(2, {3})= c23+d(3, {})=2+3=5(2→3) d(2, {1})= c21+d(1, {})=4+5=9(2→1)
d(3, {1})= c31+d(1, {})=7+5=12(3→1) d(3, {2})= c32+d(2, {})=5+6=11(3→2)
再向前倒退，有：
d(1, {2, 3})= min{c12+d(2, {3}), c13+ d(3, {2})}=min{2+5, 3+11}=7(1→2)
d(2, {1, 3})=min{c21+d(1, {3}), c23+ d(3, {1})}=min{4+6, 2+12}=10(2→1)
d(3, {1, 2})=min{c31+d(1, {2}), c32+ d(2, {1})}=min{7+8, 5+9}=14(3→2)
最后有：
d(0, {1, 2, 3})=min{c01+ d(1, { 2, 3}), c02+ d(2, {1, 3}), c03+ d(3, {1, 2})}
=min{3+7, 6+10, 7+14}=10(0→1)
所以，从顶点0出发的TSP问题的最短路径长度为10，路径是0→1→2→3→0。

动态规划法求解TSP问题的填表过程
假设n个顶点用0～n-1的数字编号，首先生成1～n-1个元素的子集存放在数组V[2n-1]中，设数组d[n][2n-1]存放迭代结果，其中d[i][j]表示从顶点i经过子集V[j]中的顶点一次且仅一次，最后回到出发点0的最短路径长度。(从顶点0出发)
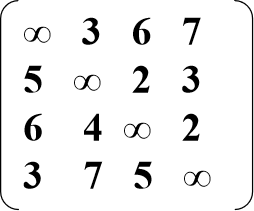
城市代价矩阵
在这里插入图片描述

代码实现

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
#define MAX_IN 10class Tsp
{
private:int city_number;		//城市个数int **distance;			//城市距离矩阵int **process;			//求最短路径的过程矩阵
public:Tsp(int city_number);		//构造函数void correct();			//矫正输入的城市代价矩阵void printCity();		//打印城市的距离矩阵void getShoretstDistance();	//动态规划法求最短路径void printProcess();		//打印过程矩阵};//构造函数
Tsp::Tsp(int city_num)
{int i = 0, j = 0;city_number = city_num;//初始化城市距离矩阵distance = new int*[city_number];cout << "请输入" << city_number << "个城市之间的距离" << endl;for (i = 0; i<city_number; i++){distance[i] = new int[city_number];for (j = 0; j<city_number; j++)cin >> distance[i][j];}//生成过程矩阵process = new int*[city_number];for (i = 0; i<city_number; i++){process[i] = new int[1 << (city_number - 1)];}}//纠正用户输入的城市代价矩阵
void Tsp::correct()
{int i;for (i = 0; i<city_number; i++){distance[i][i] = 0;}
}//打印城市距离
void Tsp::printCity()
{int i, j;//打印代价矩阵cout << "您输入的城市距离如下" << endl;for (i = 0; i<city_number; i++){for (j = 0; j<city_number; j++)cout << setw(3) << distance[i][j];cout << endl;}
}//动态规划法求最短路径
void Tsp::getShoretstDistance()
{int i, j, k;//初始化第一列for (i = 0; i<city_number; i++){process[i][0] = distance[i][0];}//初始化剩余列for (j = 1; j<(1 << (city_number - 1)); j++){for (i = 0; i<city_number; i++){process[i][j] = 0x7ffff;//设0x7ffff为无穷大//对于数字x，要看它的第i位是不是1，通过判断布尔表达式 (((x >> (i - 1) ) & 1) == 1的真值来实现if (((j >> (i - 1)) & 1) == 1){continue;}for (k = 1; k<city_number; k++){//不能达到k城市if (((j >> (k - 1)) & 1) == 0){continue;}if (process[i][j]>distance[i][k] + process[k][j ^ (1 << (k - 1))]){process[i][j] = distance[i][k] + process[k][j ^ (1 << (k - 1))];//cout<<i<<"行"<<j<<"列为："<<process[i][j]<<endl;}}}}cout << "最短路径为" << process[0][(1 << (city_number - 1)) - 1] << endl;}//打印过程矩阵
void Tsp::printProcess()
{int i, j;for (j = 0; j<1 << (city_number - 1); j++){cout << setw(3) << j;}cout << endl;for (i = 0; i<city_number; i++){for (j = 0; j<1 << (city_number - 1); j++){if (process[i][j] == 0x7ffff)process[i][j] = -1;cout << setw(3) << process[i][j];}cout << endl;}
}//主函数
int main(void)
{int city_number;while (cin >> city_number){Tsp tsp(city_number);		//初始化城市代价矩阵tsp.correct();					//纠正用户输入的代价矩阵tsp.printCity();				//打印城市tsp.getShoretstDistance();		//求出最短路径tsp.printProcess();			//打印计算矩阵}return 0;
}