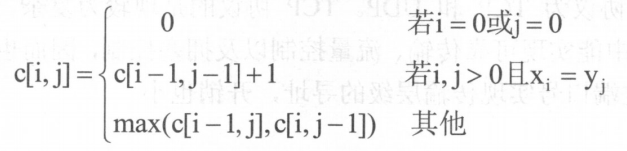实验目的

实验内容

实验步骤

一、最长公共子序列

二、矩阵连乘

实验目的

加深对动态规划法的算法原理及实现过程的理解，学习用动态规划法解决实际应用中的最长公共子序列问题和矩阵连乘问题，体会动态规划法和备忘录方法的异同。

实验内容

一、用动态规划法和备忘录方法实现求两序列的最长公共子序列问题。要求掌握动态规划法思想在实际中的应用，分析最长公共子序列的问题特征，选择算法策略并设计具体算法，编程实现两输入序列的比较，并输出它们的最长公共子序列。

二、用动态规划法和备忘录方法求解矩阵相乘问题，求得最优的计算次序以使得矩阵连乘总的数乘次数最少，并输出加括号的最优乘法算式。

实验步骤

一、最长公共子序列

1、最长公共子序列（Longest Common Subsequence,LCS）问题是：给定两个字符序列 $\mathbf{\textbf{}X=\left \{ x_{1}, x_{2} ,......, x_{m}\right \}}$ 和 $\mathbf{\textbf{}Y=\left \{ y_{1}, y_{2} ,......, y_{m}\right \}}$ ，要求找出 A 和 B 的一个最长公共子序列。例如： $\mathbf{\textbf{}X=\left \{ a,b,c,b,d,a,b\right \}}$ ， $\mathbf{\textbf{}Y=\left \{ b,d,c,a,b,a\right \}}$ 。它们的最长公共子序列 $\mathbf{ LSC=\left \{ b,c,b,a \right \}}$ 。通过“穷举法”列出 X 的所有子序列，检查其是否为 Y 的子序列并记录最长公共子序列的长度这种方法，求解时间为指数级的，因此不可取。

2、分析 LCS 问题特征可知，如果 $\mathbf{\textbf{}Z=\left \{ z_{1},z_{2},......,z_{k} \right \}}$ 为它们的最长公共子序列，则它们一定具有以下性质：

(1)若 $\mathbf{x_{m}=y_{n}}$ ，则 $\mathbf{z_{k}=x_{m}=y_{n}}$ ，且 $\mathbf{Z_{k-1}}$ 是 $\mathbf{X_{m-1}}$ 和 $\mathbf{Y_{n-1}}$ 的最长公共子序列；

(2)若 $\mathbf{x_{m}\neq y_{n}}$ 且 $\mathbf{z_{k}\neq x_{m}}$ ，则 $\boldsymbol{Z \mathbf{}}$ 是 $\mathbf{X_{m-1}}$ 和 $\textbf{Y\textbf{}}$ 的最长公共子序列；

(3)若 $\mathbf{x_{m}\neq y_{n}}$ 且 $\mathbf{z_{k}\neq y_{n}}$ ，则 $\boldsymbol{Z \mathbf{}}$ 是 $\mathbf{X}$ 和 $\mathbf{Y_{n-1}}$ 的最长公共子序列。

这样就将求 $\mathbf{X\mathbf{}}$ 和 $\mathbf{Y}$ 的最长公共子序列问题，分解为求解较小规模的子问题：

$\bigstar$ 若 $\mathbf{x_{m}=y_{n}}$ ，则进一步分解为求解两个（前缀）子字符序列 $\mathbf{X_{m-1}}$ 和 $\mathbf{Y_{n-1}}$ 的最长公共子序列问题；

$\bigstar$ 如果 $\mathbf{x_{m}\neq y_{n}}$ ，则原问题转化为求解两个子问题，即找出 $\mathbf{X_{m-1}}$ 和 $\textbf{Y\textbf{}}$ 的最长公共子序列与找出 $\mathbf{X}$ 和 $\mathbf{Y_{n-1}}$ 的最长公共子序列，取两者中较长者作为 $\mathbf{X\mathbf{}}$ 和 $\mathbf{Y}$ 的最长公共子序列。

由此可见，两个序列的最长公共子序列包含了这两个序列的前缀的最长公共子序列，具有最优子结构性质。

3、令c[i][j]保存字符序列 $\mathbf{\textbf{}X_{i}=\left \{ x_{1}, x_{2} ,......, x_{i}\right \}}$ 和 $\mathbf{\textbf{}X_{j}=\left \{ x_{1}, x_{2} ,......, x_{j}\right \}}$ 的最长公共子序列的长度。由上述分析可得如下递推式：

$\mathbf{c[i][j]=\left\{\begin{matrix} 0 &i=0\, \, \, \, or\, \, \, \, j=0 \\ c[i-1][j-1]+1&i,j>0\, \, \, \, and\, \, \, \, x_{i}=y_{j} \\ max\left \{ c[i][j-1],c[i-1][j] \right \}& i,j>0\, \, \, \, and\, \, \, \, x_{i}\neq y_{j} \end{matrix}\right.}$

由此可见，最长公共子序列的求解具有重叠子问题性质，如果采用递归算法实现，会得到一个指数时间算法。因此需要采用动态规划法自底向上求解，并保存子问题的解，这样可以避免重复计算子问题，在多项式时间内完成计算。

4、为了能由最优解值进一步得到最优解（即最长公共子序列），还需要一个二维数组 s[][]，数组中的元素 s[i][j]记录 c[i][j]的值是由三个子问题 c[i-1][j-1]+1,c[i][j-1]和 c[i-1][j]中的哪一个计算得到，从而可以得到最优解的当前解分量（即最长公共子序列中的当前字符），最终构造出最长公共子序列自身。

5、计算最长公共子序列长度，并给出最长公共子序列：

（注意：C 语言中数组下标由 0 开始，而实际数据在一维数组 a、b 和二维数组 c、s 中的存放却是从下标为 1 处开始。)

二维数组 c 和 s 用于动态规划法求解过程中保存子问题的求解结果，一维数组 a 和 b 用于存放两个字符序列，m 和 n 为两个字符序列中实际字符的个数。

#include <iostream>
#include <cstring>
#define MAX 1024
using namespace std;int m,n;
string a,b;
int c[MAX][MAX],s[MAX][MAX];int LCSLength() {for(int i=1; i<=m; i++) {for(int j=1; j<=n; j++) {if(a[i]==b[j]) {c[i][j]=c[i-1][j-1]+1;s[i][j]=1;} else if(c[i][j-1]>c[i-1][j]) {c[i][j]=c[i][j-1];s[i][j]=2;} else {c[i][j]=c[i-1][j];s[i][j]=3;}}}return c[m][n];
}void CLCS(int i,int j) {if(s[i][j]==0)  return;if(s[i][j]==1) {CLCS(i-1,j-1);cout << a[i];} else if(s[i][j]==2) {CLCS(i,j-1);} else if(s[i][j]==3) {CLCS(i-1,j);}
}int main() {cin >> a >> b;m = a.length();n = b.length();a = '0'+a;b = '0'+b;for(int i=0; i<=m; i++)for(int j=0; j<=n; j++)c[i][j]=0,s[i][j]=0;cout << "最长公共子序列长度是:" << LCSLength() << endl;		cout << "最长公共子序列为:";CLCS(m,n);return 0;
}

7、输入序列 $\mathbf{\textbf{}X=\left \{ x_{1}, x_{2} ,......, x_{m}\right \}=\left \{ a,b,c,b,d,a,b \right \}}$ 和 $\mathbf{\textbf{}Y=\left \{ y_{1}, y_{2} ,......, y_{n}\right \}=\left \{ b,d,c,a,b,a \right \}}$ 作为测试数据，测试程序是否能够正确运行？输出结果是什么？

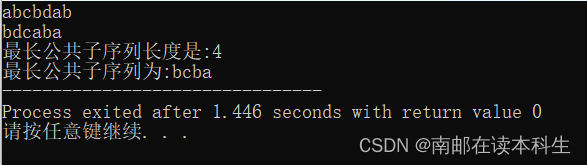
8、分析该动态规划算法的两个主要成员函数 int LCSLength()和 void CLCS()的时间复杂性。

$O\left ( m\times n \right ),O(m+n)$

二、矩阵连乘

1、求解目标若 n 个矩阵 $\left \{ A_{1} ,A_{2},.....A_{n}\right \}$ 中两个相邻矩阵 $A_{i}$ 和 $A_{i+1$ 均是可乘的， $A_{i}$ 的维数为 $p_{i}p_{i+1}$ ， $A_{i+1}$ 的维数为 $p_{i+1} p_{i+2}$ 。求 n 个矩阵 $\left \{ A_{1} ,A_{2},.....A_{n}\right \}$ 连乘时的最优计算次序，以及对应的最少数乘次数。两矩阵相乘 $A_{i}A_{i+1}$ 做 $p_{i}p_{i+1}p_{i+2}$ 次数乘，可得 $p_{i}p_{i+2}$ 的结果矩阵。而矩阵连乘 $\left \{ A_{i} ,A_{i+1},.....A_{j}\right \}$ （简记为 A[i：j]）求得 $p_{i}p_{i+1}$ 的结果矩阵时，采用不同的计算次序，对应的总数乘次数也不同。

2、例如：4 个矩阵连乘 $A_{1}A_{2}A_{3}A_{4}$ ，其中 $A_{1}$ 的维数：50×10， $A_{2}$ 的维数：10×40， $A_{3}$ 的维数： 40×30， $A_{4}$ 的维数：30×5。有 5 种不同的计算次序：

次序 1： $\left ( \left ( \left ( A_{1} A_{2} \right ) A_{3} \right ) A_{4} \right )$ 需要 50×10×40+50×40×30+50×30×5=87500 次

次序 2： $((A_{1} A_{2}) (A_{3} A_{4} ))$ 需要 50×10×40+40×30×5+50×40×5=36000 次

次序 3： $((A_{1} (A_{2} A_{3}) )A_{4} )$ 需要 10×40×30+50×10×30+50×30×5=34500 次

次序 4： $(A_{1}((A_{2} A_{3}) A_{4} ))$ 需要 10×40×30+10×30×5+50×10×5=16000 次

次序 5： $( A_{1} (A_{2}( A_{3} A_{4} )))$ 需要 40×30×5+10×40×5+50×10×5=10500 次

3、将二维数组 m[i][j]定义为：计算 A[i：j]所需的最少数乘次数；

二维数组 s[i][j]定义为：计算 A[i：j]的最优计算次序中的断开位置（例如：若计算 A[i： j]的最优次序在 $A_{k}$ 和 $A_{k+1}$ 之间断开,i≤k<j,则 s[i][j]=k）。

4、当 i=j 时，A[i：j]=Ai是单一矩阵，无须计算，因此 m[i][j]=0；

当 i<j 时， $m[i][j]=min\left \{ m[i][k]+m[k+1][j]+p_{i}p_{k+1}p_{j+1} \right \} (i\leqslant k<j)$

5、算法思路

因为计算 m[i][j]时，只用到已计算出的 m[i][k]和 m[k+1][j]。所以首先计算出 m[i][i]=0， i=1,2,……n；然后再根据递归式，按矩阵链长递增的方式依次计算 m[i][i+1]，i=1，2，…n-1（矩阵链长度为 2）；m[i][i+2]，i=1，2，…n-2（矩阵链长度为 3）；……则 m[1][n]就是问题的最优解值（最少数乘次数）。

要构造问题的最优解，根据 s 数组可推得矩阵乘法的次序。从 s[1][n]可知计算 A[1：n] 的最优加括号方式为(A[1：s[1][n]])(A[s[1][n]+1：n])。其中 A[1：s[1][n]]的最优加括号方式又为（A[1：s[1][s[1][n]]]）(A[s[1][s[1][n]]+1：s[1][n]])。……照此递推下去，最终可以确定 A[1：n]的最优完全加括号方式，构造出问题的一个最优解。

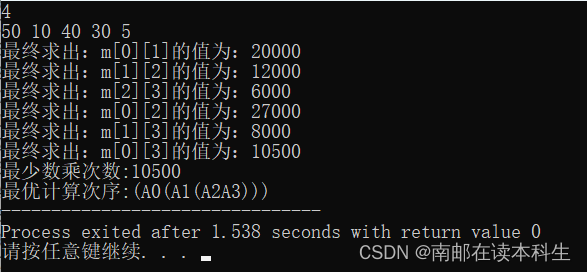
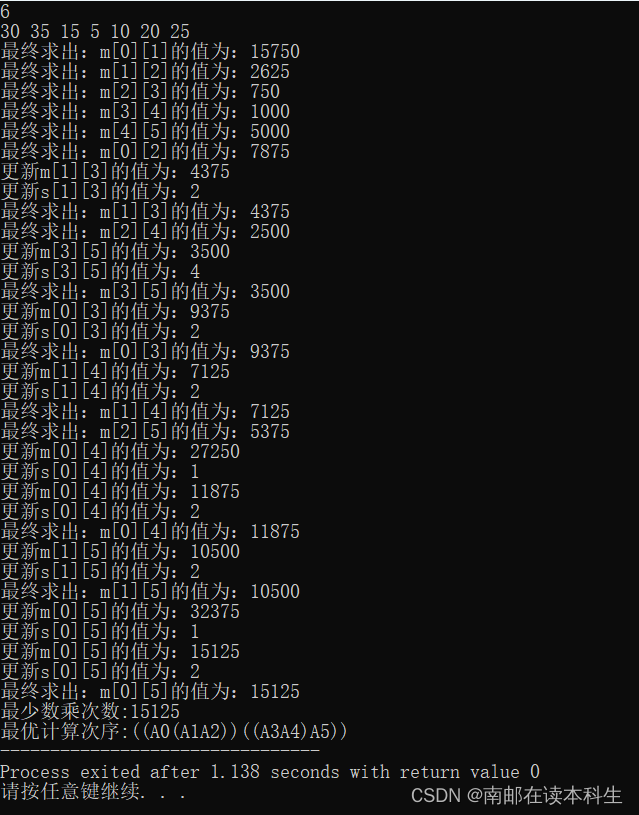
6、动态规划法实现的算法提示（请分别对实例 1： $A_{1}$ 维数：50×10， $A_{2}$ 维数：10×40， $A_{3}$ 维数：40×30， $A_{4}$ 维数： 30×5 和实例 2： $A_{1}$ 维数：30×35， $A_{2}$ 维数：35×15， $A_{3}$ 维数：15×5， $A_{4}$ 维数：5×10； $A_{5}$ 维数：10×20， $A_{6}$ 维数：20×25 分别求解。）

#include <iostream>
#include <cstring>
#define MAX 1024
using namespace std;int n;
int p[MAX];
int m[MAX][MAX],s[MAX][MAX];int MChain() {for(int r=1; r<n; r++) {for(int i=0; i<n-r; i++) {int j = i+r;m[i][j]=m[i][i]+m[i+1][j]+p[i]*p[i+1]*p[j+1];s[i][j]=i;for(int k=i+1; k<j; k++) {int t = m[i][k]+m[k+1][j]+p[i]*p[k+1]*p[j+1];if(t<m[i][j]) {m[i][j]=t;cout<<"更新m["<<i<<"]["<<j<<"]的值为："<<t<<endl;s[i][j]=k;cout<<"更新s["<<i<<"]["<<j<<"]的值为："<<k<<endl;}}cout<<"最终求出：m["<<i<<"]["<<j<<"]的值为："<<m[i][j]<<endl;}}return m[0][n-1];
}void Traceback(int i,int j) {if(i==j) {cout << 'A' << i;return ;}if(i<s[i][j]) cout << '(';Traceback(i,s[i][j]);if(i<s[i][j]) cout << ')';if(s[i][j]+1<j) cout << '(';Traceback(s[i][j]+1,j);if(s[i][j]+1<j) cout << ')';
}int main() {cin >> n;for(int i=0; i<=n; i++) {cin>>p[i];}for(int i=0; i<n; i++) {m[i][i] = 0;s[i][i]=i;}cout << "最少数乘次数:" <<  MChain() << endl;cout << "最优计算次序:" << '(';Traceback(0,n-1);cout << ')';return 0;
}