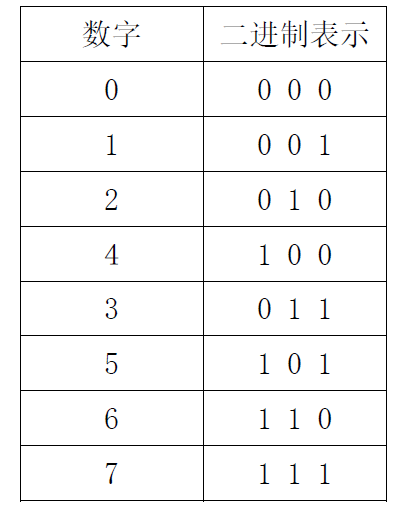
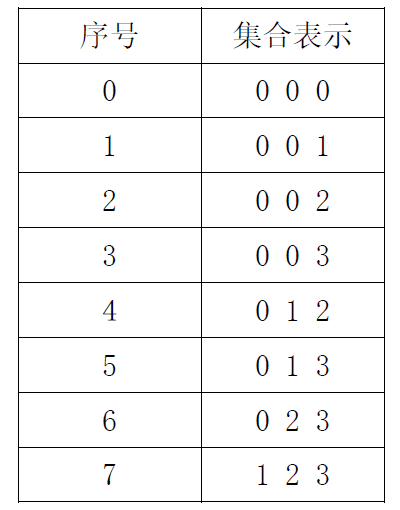
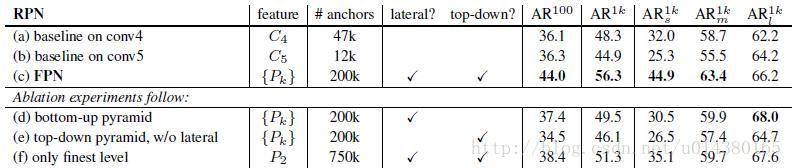
TSP问题是指旅行家要旅行n个城市,要求各个城市经历且仅经历一次然后回到出发城市,并要求所走的路程最短。各个城市间的距离可以用代价矩阵来表示。
假设从顶点i出发,令d(i, V')表示从顶点i出发经过V'中各个顶点一次且仅一次,最后回到出发点i的最短路径长度,开始时,V'=V-{i},于是,TSP问题的动态规划函数为:d(i,V')=min{cik+d(k,V-{k})}(k∈V')
d(k,{})=cki(k≠i)
伪代码:
for (i=1; i<n; i++) //初始化第0列d[i][0]=c[i][0]; for (j=1; j<2n-1-1; j++) for (i=1; i<n; i++) //依次进行第i次迭代if (子集V[j]中不包含i) 对V[j]中的每个元素k,计算[i][j]=min(c[i][k]+d[k][j-1]);
对V[2n-1-1]中的每一个元素k,计算d[0][2n-1-1]=min(c[0][k]+d[k][2n-1-2]);
输出最短路径长度d[0][2n-1-1];
笔者在写此程序时卡在了如何判断:子集V[j]中不包含i。解决方法是对n个顶点分别用0~n-1的数字编号,按个数为1,2,……,n-1的顺序生成1~n-1个元素的子集存放在数组V[2^n-1]中。这样,在判断时就可以将当前点与数组编号按位与运算(如下图所示),为0则为需要进行计算(这时才能品味按位与运算的美)。
完整代码:
#include<iostream.h>
#include<math.h>
int main()
{int i,j,k,min,brief,n;int D[20][20];cout<<"顶点个数:";cin>>n;int b=(int)pow(2,n-1);for(i=0;i<n;i++)for(j=0;j<n;j++)cin>>D[i][j];int ** Route = (int **)calloc(n, sizeof(int *));int ** Mat = (int **)calloc(n, sizeof(int *));for(i=0;i<n;i++){Route[i] = (int *)calloc(b*b, sizeof(int))+i*b;Mat[i] = (int *)calloc(b*b, sizeof(int))+i*b;}for(i=0;i<b;i++)for(j=0;j<n;j++){Route[j][i] = -1;Mat[j][i] = -1;}for(i=0;i<n;i++)//初始化第0列 Route[i][0] = D[i][0]; for(i=1;i<b-1;i++)for(j=1;j<n;j++)//依次进行第i次迭代 if( ((int)pow(2,j-1) & i) == 0)//子集V[j不包含i {min=999;for(k=1;k<n;k++)if( (int)pow(2,k-1) & i ){brief = D[j][k] + Route[k][i-(int)pow(2,k-1)]; if(brief < min){min = brief;Route[j][i] = min;Mat[j][i] = k;//局部最优决策}} }min=999;for(k=1;k<n;k++){brief = D[0][k] + Route[k][b-1 - (int)pow(2,k-1)];if(brief < min){min = brief;Route[0][b-1] = min;//最优解Mat[0][b-1] = k;}}cout<<"最短路径长度:"<<Route[0][b-1]<<endl;//最短路径长度cout<<"最短路径:"<<"1";for(i=b-1,j=0; i>0; ){j = Mat[j][i];i = i - (int)pow(2,j-1);cout<<"->"<<j+1;}cout<<"->1"<<endl;for(i=0;i<n;i++){for(j=0;j<b;j++)cout<<Route[i][j]<<" ";cout<<endl;}free(Route);free(Mat);return 0;
}