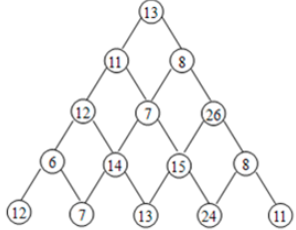
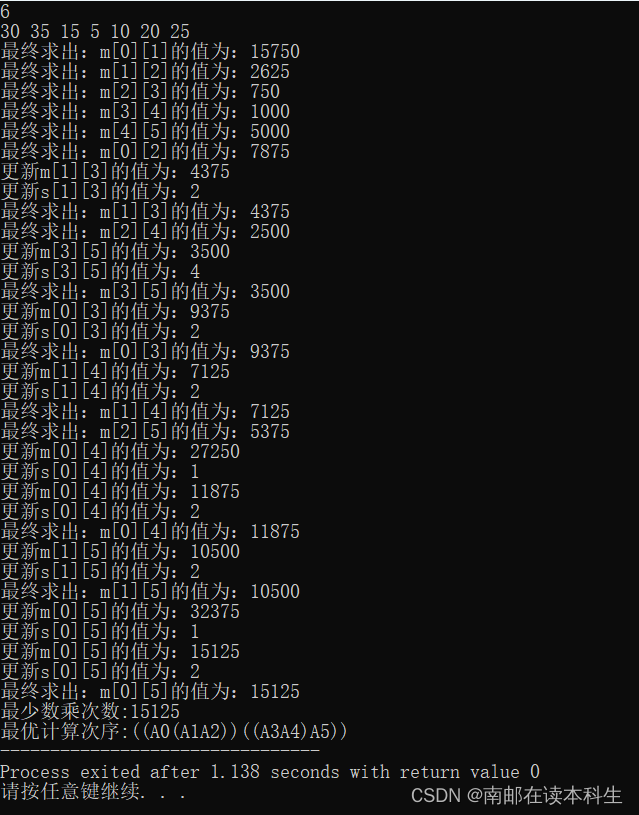
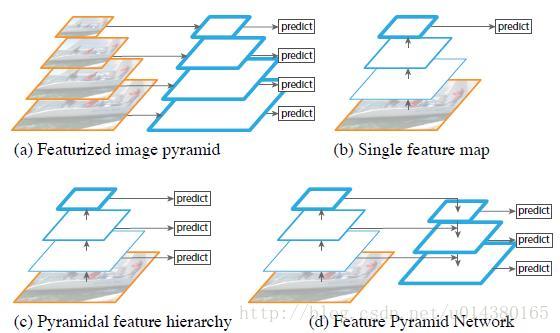
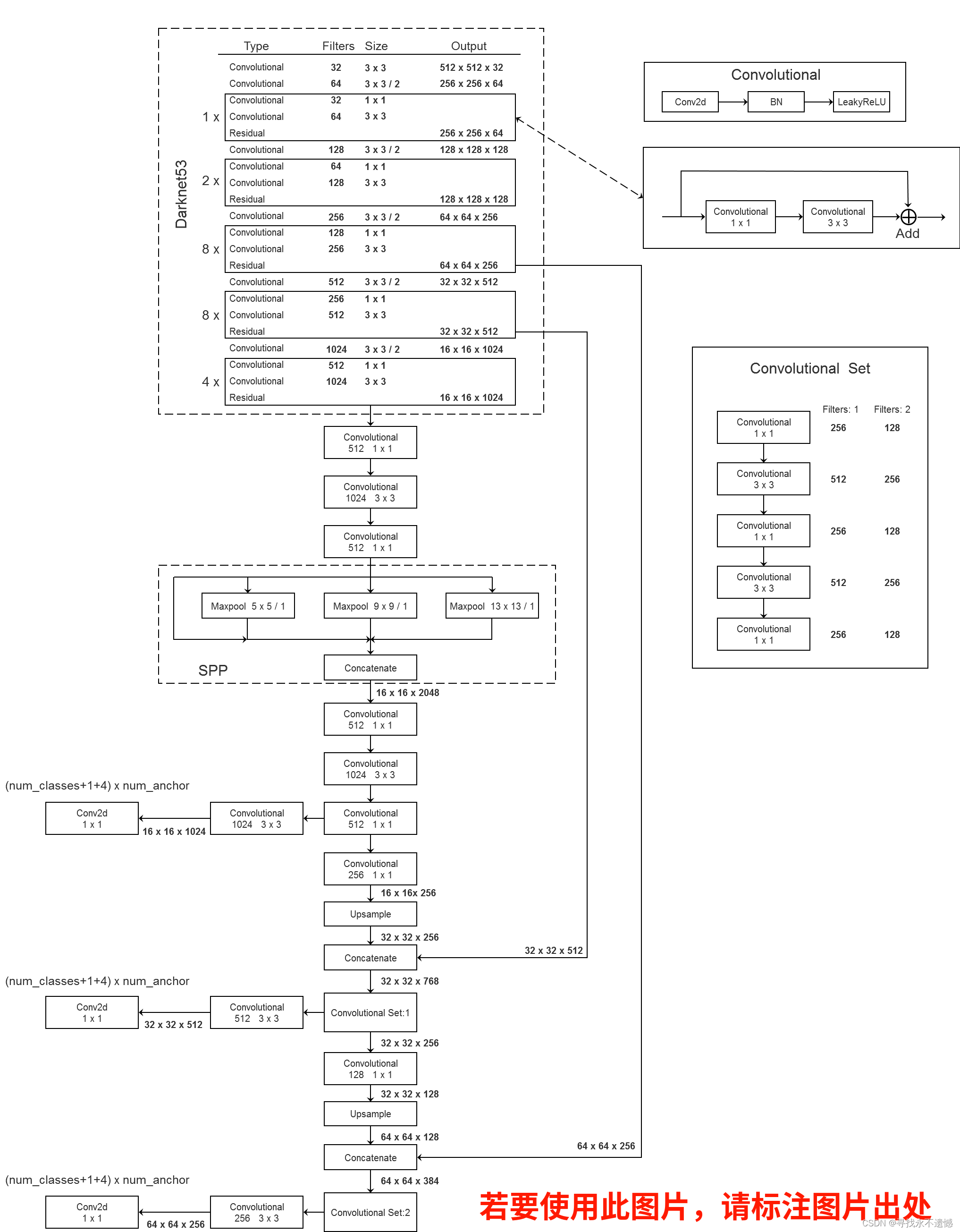
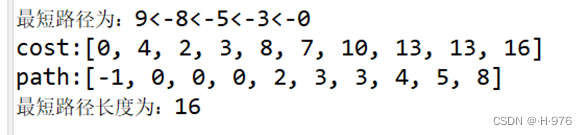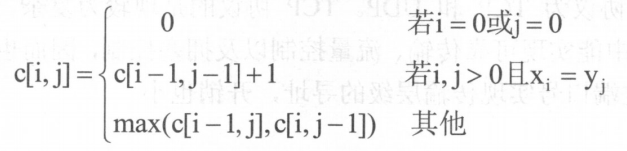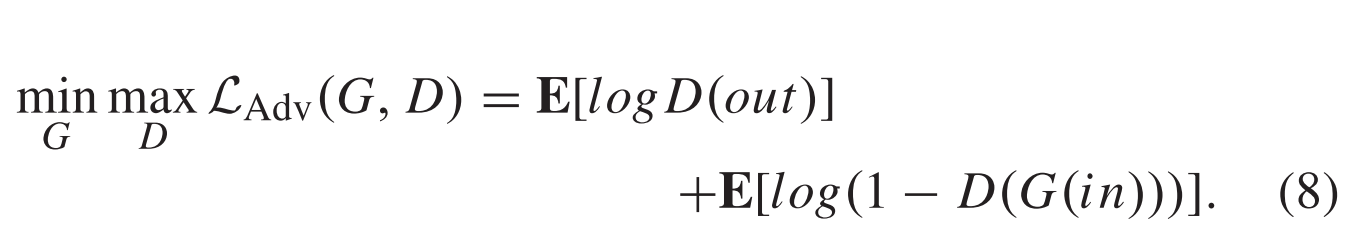动态规划法求解0/1背包问题

article/2025/9/29 20:06:24

一、求解0/1背包问题
1、问题描述
有n个重量分别为{w1，w2，…，wn}的物品，它们的价值分别为{v1，v2，…，vn}，给定一个容量为C的背包。
设计从这些物品中选取一部分物品放入该背包的方案，每个物品要么选中要么不选中，要求选中的物品的总重量不能超过背包的容量，求具有最大的价值的装载方案。
2、蛮力法求解
在这里插入图片描述

3、证明0/1背包问题满足最优性原理

4、问题分析
（1）第1步问题结构分析（划分子问题）

（2）第2步确定动态规划函数

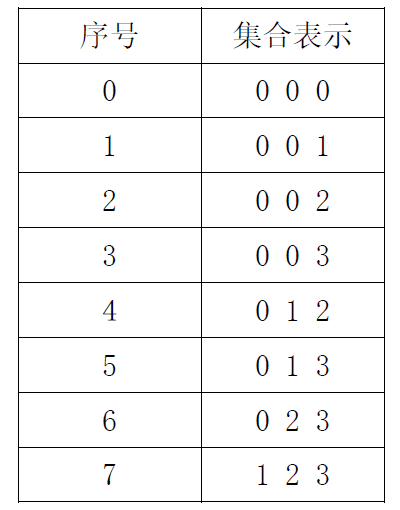
（3）第3步设计表格，填表

比如：

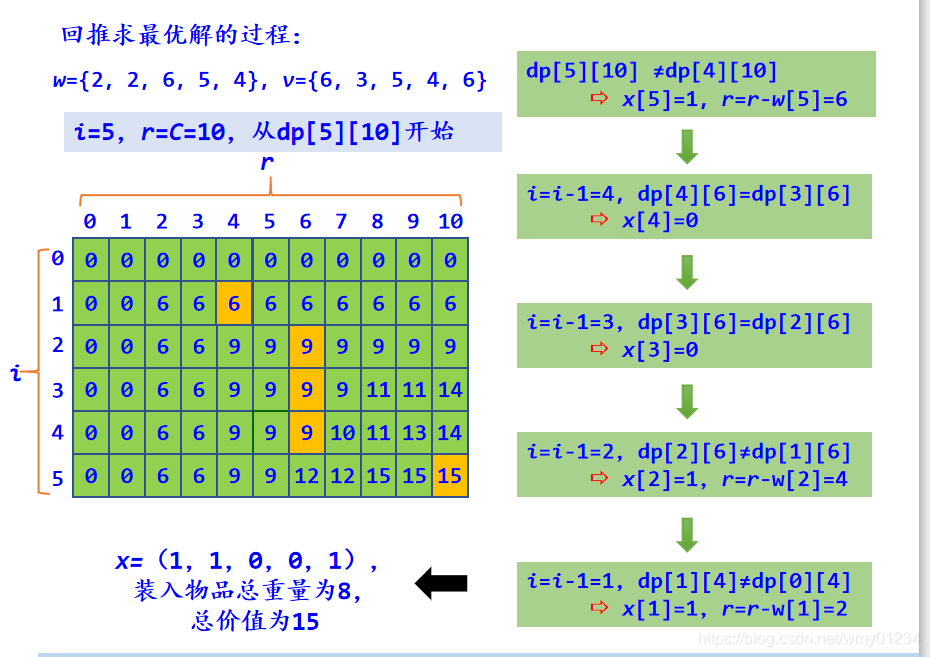
5、算法设计

//问题表示
int n=5，C=10;  //5种物品，限制重量不超过10
int w[MAXN]={0，2，2，6，5，4}; //下标0不用
int v[MAXN]={0，6，3，5，4，6}; //下标0不用
//求解结果表示
int dp[MAXN][MAXW];
int x[MAXN];
int maxv;    //存放最优解的总价值
void Knapsack()   //动态规划法求0/1背包问题
{  int i，r;for (i=0;i<=n;i++)  //置边界条件dp[i][0]=0dp[i][0]=0;for (r=0;r<=C;r++)  //置边界条件dp[0][r]=0dp[0][r]=0;for (i=1;i<=n;i++){  for (r=1;r<=C;r++)if (r<w[i])dp[i][r]=dp[i-1][r];elsedp[i][r]=max(dp[i-1][r]，dp[i-1][r-w[i]]+v[i]);}
}
void Buildx()    //回推求最优解
{  int i=n，r=C;maxv=0;while (i>=0)   //判断每个物品{if (dp[i][r]!=dp[i-1][r]) {  x[i]=1;   //选取物品imaxv+=v[i];   //累计总价值r=r-w[i];}elsex[i]=0;   //不选取物品ii--;}
}

6、算法分析
Knapsack()算法中含有两重for循环，所以时间复杂度为O(n×C)，空间复杂度为O(n×C)。
7、滚动数组求解0/1背包问题
在这里插入图片描述

8、练习
用动态规划法求解0/1背包问题：n=5, C=17 ，物品重量和价值分别是：w={3,4,7,8,9}和 v={4,5,10,11,13}，求最优值和最优解,写出填表求解过程。