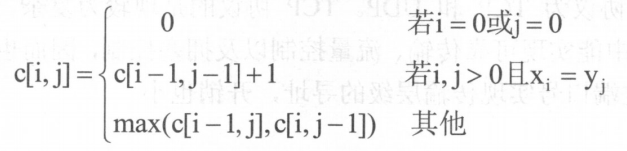问题描述
有5个物品,其重量分别是{2, 2, 6, 5, 4},价值分别为{6, 3, 5, 4, 6},背包的容量为10,计算背包所能装入物品的最大价值。
求解思路
在0/1背包问题中,物品i或者被装入背包,或者不被装入背包,设xi表示物品i装入背包的情况,则当xi=0时,表示物品i没有被装入背包,xi=1时,表示物品i被装入背包。根据问题的要求,有如下约束条件和目标函数:
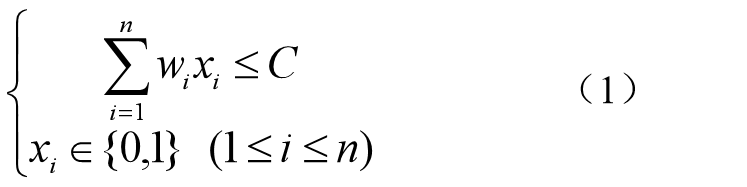

于是,问题归结为寻找一个满足约束条件式1,并使目标函数式2达到最大的解向量X=(x1, x2, …, xn)。
0/1背包问题可以看作是决策一个序列(x1, x2, …, xn),对任一变量xi的决策是决定xi=1还是xi=0。按下述方法来划分阶段:第一阶段,只装入前1个物品,确定在各种情况下的背包能够得到的最大价值;第二阶段,只装入前2个物品,确定在各种情况下的背包能够得到的最大价值;依此类推,直到第n个阶段。
实现过程
决策序列(x1, x2, …, xn),对任一变量xi的决策是决定xi=1还是xi=0。在对xi-1决策后,已确定了(x1, …, xi-1),在决策xi时,第i个物品则会有以下两种情况:
(1)如果第i个物品没有装入背包,则背包中物品的价值就等于把前i-1个物品装入容量为j的背包中所取得的价值。
(2)如果把第i个物品装入背包,则背包中物品的价值等于把前i-1个物品装入容量为j-wi的背包中的价值加上第i个物品的价值vi。
设V(n, C)表示将n个物品装入容量为C的背包获得的最大价值,显然,初始子问题是把前面i个物品装入容量为0的背包和把0个物品装入容量为j的背包,得到的价值均为0,即:
V(i, 0)= V(0, j)=0 (0≤i≤n, 0≤j≤C)
考虑原问题的一部分,设V(i, j)表示将前i(1≤i≤n)个物品装入容量为j(1≤j≤C)的背包获得的最大价值,在决策xi 时,可采用递推式:
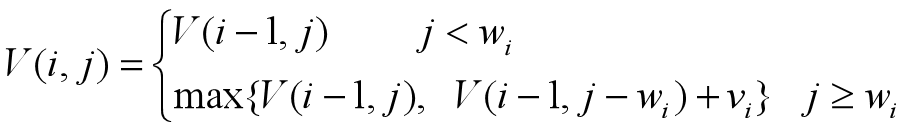
得到如下动态规划函数:V(i, 0)= V(0, j)=0
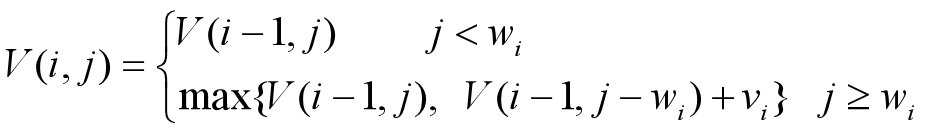
第二个式子表明:如果第i个物品的重量小于背包的容量,则会有以下两种情况:
(1)如果第i个物品没有装入背包,则背包中物品的价值就等于把前i-1个物品装入容量为j的背包中所取得的价值。
(2)如果把第i个物品装入背包,则背包中物品的价值等于把前i-1个物品装入容量为j-wi的背包中的价值加上第i个物品的价值vi;
显然,取二者中价值较大者作为把前i个物品装入容量为j的背包中的最优解。
在每个阶段的决策中,始终保持当前所完成的决策(序列)使得背包的价值是最大的。
根据动态规划函数,用一个(n+1)×(C+1)的二维表V,V[i][j]表示把前i个物品装入容量为j的背包中获得的最大价值。
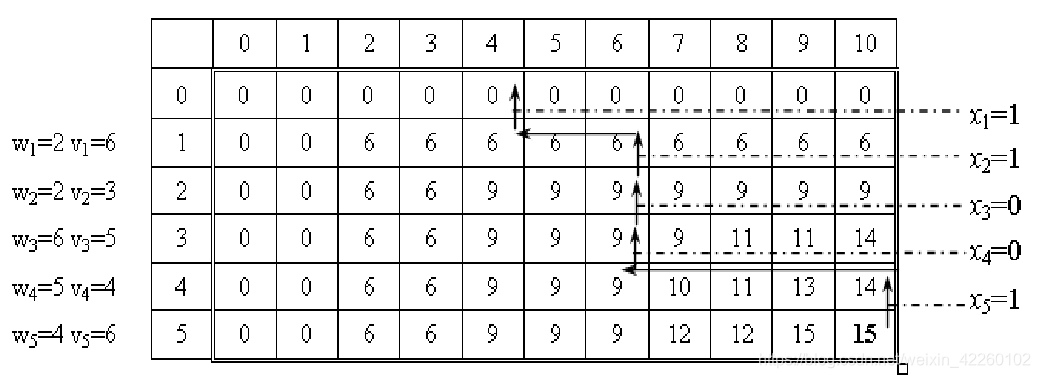
代码实现
#include<iostream>
using namespace std;#define C 10
int V[6][11];
int x[5];
int KnapSack(int n, int w[], int v[]);
int max(int x, int y);
void printV();
int main()
{int w[] = { 2, 2, 6, 5, 4 };int v[] = { 6, 3, 5, 4, 6 };cout << "背包的最大价值为:" << KnapSack(5, w, v) << endl;cout << "装入背包的物品是:";for (int i = 0; i < 5; i++){if (x[i]==1){cout << "物品" << i + 1;}}printf("\n");printV();cout << endl;return 0;
}int max(int x, int y){if (x>y){return x;}else{return y;}
}int KnapSack(int n, int w[], int v[]){int i, j;//1.初始化第0列for ( i = 0; i <=n; i++){V[i][0] = 0;}//2.初始化第0行for ( j = 0; j <=C; j++){V[0][j] = 0;}//3.初始化第i行,进行i次迭代for (i = 1; i <=n; i++){for ( j = 1; j <= C; j++){if (j<w[i-1]){//第j个物品重量大加不进去V[i][j] = V[i - 1][j];}else{V[i][j] = max(V[i - 1][j], V[i-1][j-w[i-1]]+v[i-1]);}}}//4.求装入的物品for ( j = C,i=n; i>0; i--){if (V[i][j]>V[i-1][j]){x[i-1] = 1;j = j - w[i-1];}else{x[i-1] = 0;}}//5.返回背包的最大价值return V[n][C];
}void printV(){for (int i = 0; i < 6; i++){for (int j = 0; j < C+1; j++){if (j==0){printf("%d\t", i);}else{printf("%d\t", V[i][j - 1]);}}printf("\n");}
}
运行结果
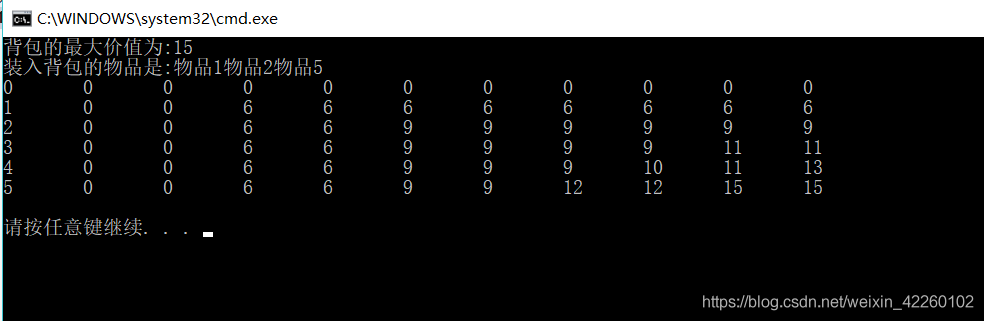
这个问题也就总结到这里,如果有什么问题的话,欢迎各位联系我~