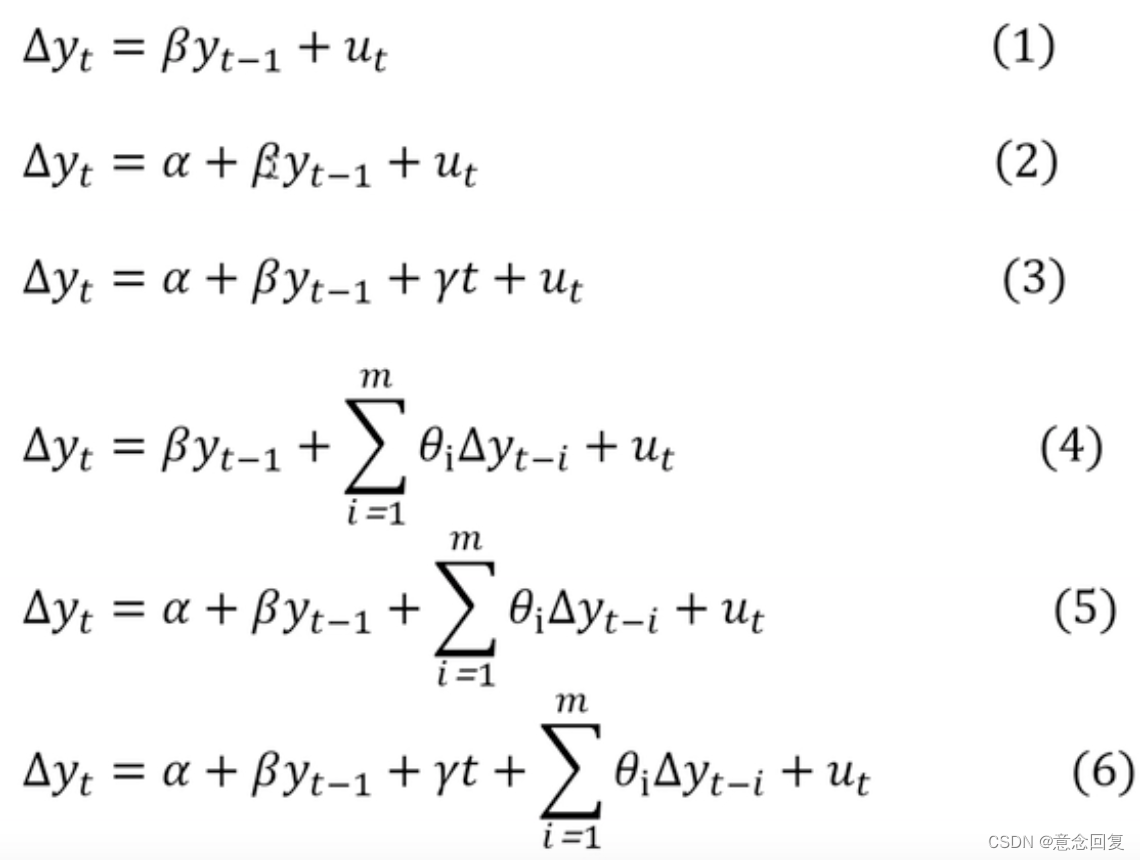上篇介绍了DF检验,该检验仅用于AR(1)过程的单位根检验,对于AR()过程来说,需要使用拓展DF检验(augmented Dickey-Fuller,ADF)。
1 模型检验形式
AR()过程的形式如下:
上式可以转换成如下形式:
而一阶检验的模型形式为:
与一阶的形式相比,p阶形式的相当于;可以看做是的滞后期,是特有的部分。
ADF检验使用的函数依然是urca工具包中的ur.df():
ur.df(y, type = c("none", "drift", "trend"),lags = 1,selectlags = c("Fixed", "AIC", "BIC"))
lag参数是指的滞后项长度的最大可能值;
type参数的设置与DF检验一致,根据是否包含截距项和时间趋势项而定;由于在进行检验前是不知道真实滞后项长度的,需要使用
selectlags参数选择确定“最佳”滞后项的原则,“最佳”滞后长度不大于lag参数所对应的值。
以下示例来自官方文档:
library(urca)
data(Raotbl3)
plot(Raotbl3$lc, type = "l")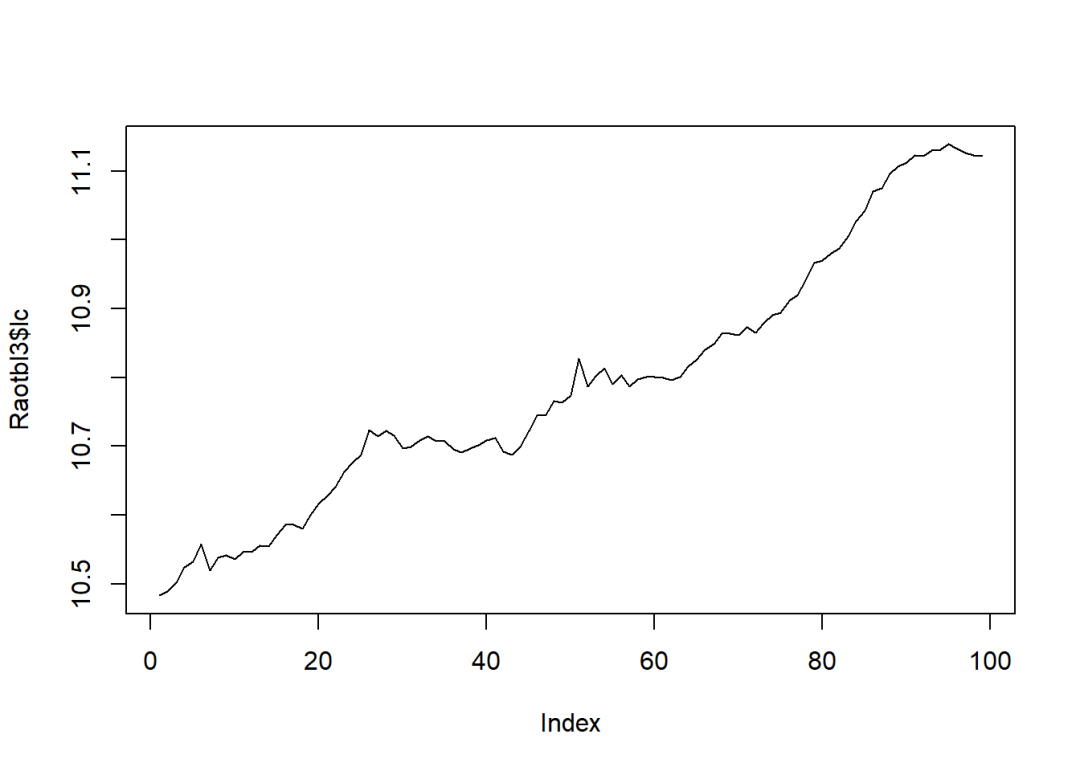
lc.df <- ur.df(y = Raotbl3$lc, lags = 12, type = 'trend',selectlags = "AIC")
summary(lc.df)
## ###############################################
## # Augmented Dickey-Fuller Test Unit Root Test #
## ###############################################
##
## Test regression trend
##
##
## Call:
## lm(formula = z.diff ~ z.lag.1 + 1 + tt + z.diff.lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.045255 -0.005840 0.000133 0.006540 0.035257
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.1215347 0.3852117 2.911 0.00472 **
## z.lag.1 -0.1068796 0.0368355 -2.902 0.00486 **
## tt 0.0006400 0.0002297 2.786 0.00674 **
## z.diff.lag1 0.0328881 0.1080263 0.304 0.76162
## z.diff.lag2 0.1374570 0.1084381 1.268 0.20881
## z.diff.lag3 0.3178508 0.1098182 2.894 0.00496 **
## z.diff.lag4 -0.1501981 0.1118817 -1.342 0.18344
## z.diff.lag5 0.2550984 0.1112869 2.292 0.02466 *
## z.diff.lag6 0.1094590 0.1152173 0.950 0.34511
## z.diff.lag7 0.2295406 0.1077044 2.131 0.03631 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.01203 on 76 degrees of freedom
## Multiple R-squared: 0.2637, Adjusted R-squared: 0.1765
## F-statistic: 3.024 on 9 and 76 DF, p-value: 0.003858
##
##
## Value of test-statistic is: -2.9015 3.7964 4.2192
##
## Critical values for test statistics:
## 1pct 5pct 10pct
## tau3 -4.04 -3.45 -3.15
## phi2 6.50 4.88 4.16
## phi3 8.73 6.49 5.47
模型输出结果中,滞后项只到
z.diff.lag7,表明按照AIC原则选择的“最优”滞后项长度为7;
tau3大于10%显著水平临界值,说明不能拒绝存在单位根的原假设,即;phi2和phi3都小于10%显著水平临界值,因此不能拒绝存在截距项和时间趋势(具体解读方法参见上篇时间序列分析(6)| DF检验)。
2 两个检验规则
研究表明,DF和ADF检验在不能拒绝存在单位根的情况下的有效性是很低的。在进行单位根假设时可以结合以下两个规则进行判断:
规则1:在回归方程中,若自变量中既有一阶单整变量,又有平稳变量,那么对于均值为0的平稳变量的系数可以使用t检验,而无需使用DF或ADF检验;
规则2:如果能够确定模型形式中包含确定性成分,即截距项或时间趋势项,那么对于该模型的所有变量的回归系数都可以使用t检验。
据此,单位根检验的一般流程如下:
DF或ADF检验有如下三种形式:形式1——不含截距项和时间趋势项;形式2——含截距项;形式3——同时含截距项和时间趋势项;
不管在哪种形式下,若DF或ADF能拒绝的原假设,则都可以认为序列不存在单位根,检验结束;若不能拒绝,由于此时检验有效性低,因此还需进一步地判断;
在形式3下,根据
phi3()判断是否能拒绝的原假设。若能拒绝,则可再使用t检验先判断是否显著异于0:如果显著异于0,则可认为序列中含有确定性的时间趋势成分,根据规则2,则可在形式3下使用t检验判断是否显著异于0,检验结束;
如果不能拒绝,或者拒绝后不能再拒绝(即不显著异于0),则需要在形式2下再进行判断;
在形式2下,根据
phi1()判断能否拒绝。若能拒绝,则可以使用t检验判断是否显著异于0:如果显著异于0,则可认为序列中含有确定性的截距成分,根据规则2,则可在形式3下使用t检验判断是否显著异于0,检验结束;
如果不能拒绝,或者拒绝后不能再拒绝(即不显著异于0),则此时只能在形式1下进行DF或ADF检验。
在第一节的示例中,所有形式下都不能拒绝的原假设,并且在形式3下不能拒绝,形式2下不能拒绝,因此只能在形式1下进行ADF检验。以下是形式2和形式1下的模型代码,各位读者可以验证。
形式2:
lc.df2 <- ur.df(y = Raotbl3$lc, lags = 12, type = 'drift',selectlags = "AIC")
summary(lc.df2)形式1:
lc.df3 <- ur.df(y = Raotbl3$lc, lags = 12, type = 'none',selectlags = "AIC")
summary(lc.df3)