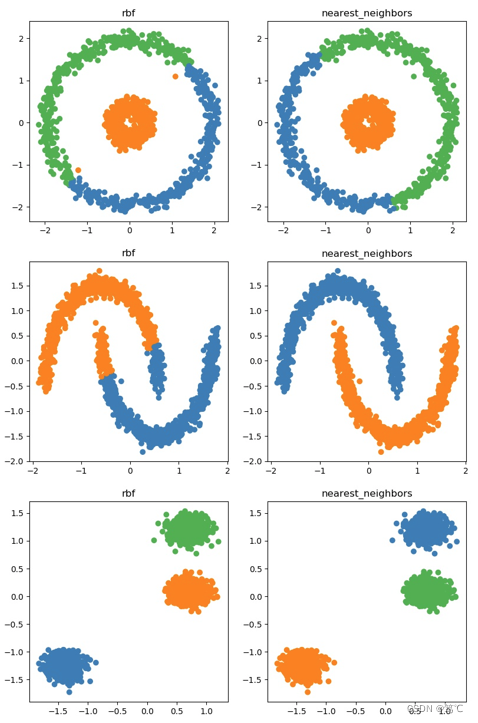
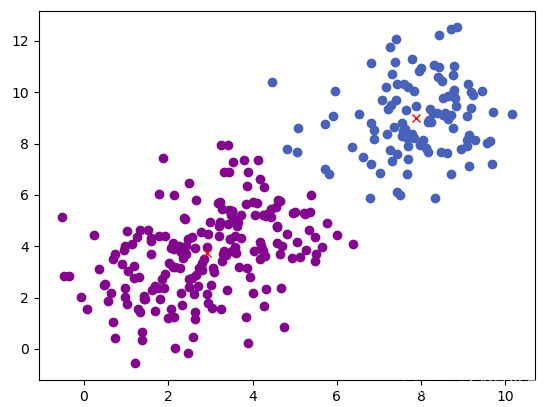
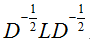k-means 可以说是思想最简单的聚类了，但是它在应对非凸数据时却显得手足无措，例如如下的数据分类：

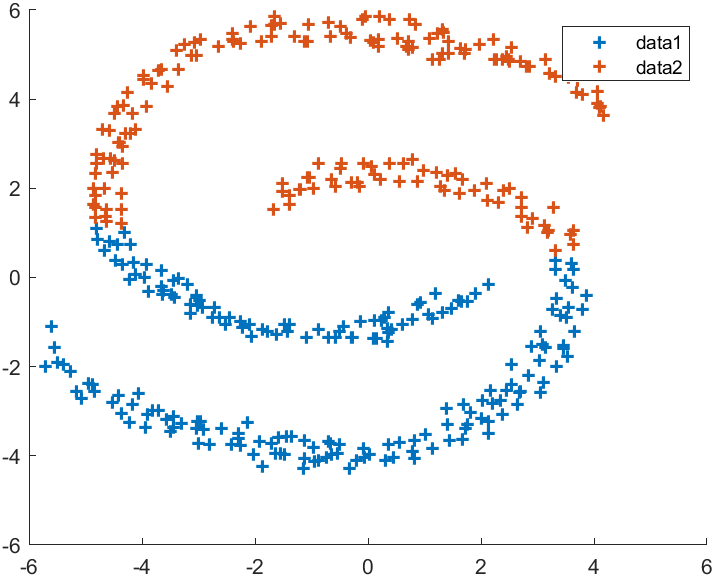
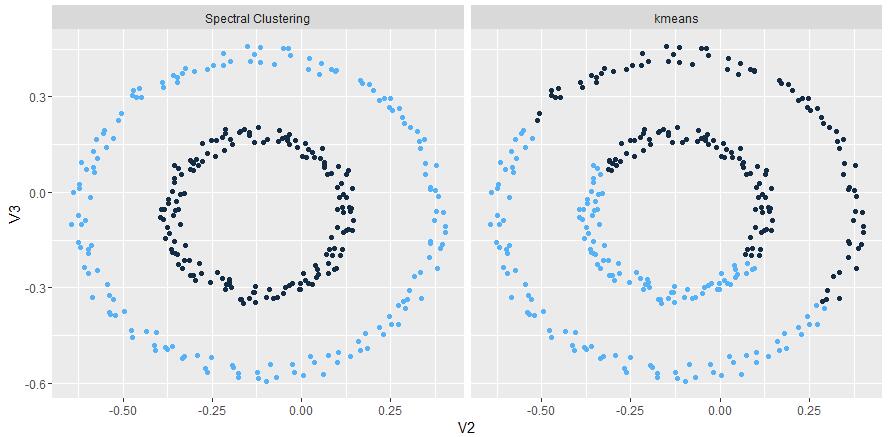
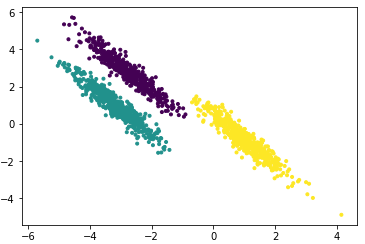
各类之间虽然间隔较远，但是非凸，这时候就需要引入谱聚类了(以下为谱聚类效果)。

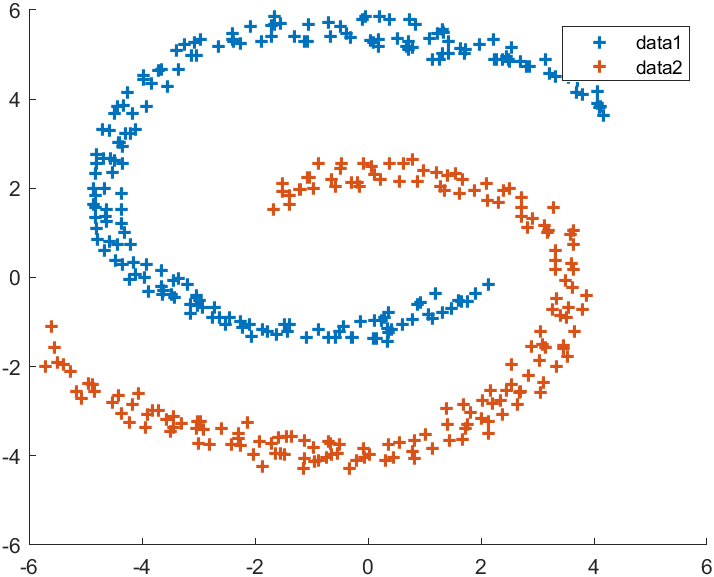
本文参考

[1]Ulrike von Luxburg. A Tutorial on Spectral Clustering[J]. CoRR,2007,abs/0711.0189(4).
[2]https://zhuanlan.zhihu.com/p/392736238
[3]https://blog.csdn.net/SL_World/article/details/104423536
[4]https://blog.csdn.net/Keeplingshi/article/details/51063190
[5]https://www.cnblogs.com/pinard/p/6221564.html

原理简述

无向图

给定一个数据集 $X=\left\{\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_n\right\}$ ，将每一个数据点看作无向图上的一个顶点，记为 $G = (V, E)$ .

相似矩阵与边权

空间两个点的距离越近，则它们越相似，距离越远，则它们越不相似，即相似度与距离成反比，这里我们提出相似矩阵的概念来衡量各个点的相似程度，其中 $w_{ij}$ 表明节点 $i$ 和节点 $j$ 的相似程度， $w_{ij}=w_{ji}$ :

$W=\left[\begin{array}{cccc} w_{11} & w_{12} & \ldots & w_{1 n} \\ w_{21} & w_{22} & \ldots & w_{2 n} \\ \vdots & \vdots & \ldots & \vdots \\ w_{n 1} & w_{n 2} & \ldots & w_{n n} \end{array}\right]$

向量空间中衡量两个点之间相似度的方法有很多，这里采用最常用的全连接法并使用高斯核函数进行衡量，即：

$w_{i j}=\exp \left(-\frac{\left\|x_i-x_j\right\|^2}{2 \sigma^2}\right)$

度与度矩阵

对角线元素 $d_i$ 是和节点 $i$ 相关的相似度之和，即：
$d_i=\sum_{j=1}^n w_{ij}$
$D=\left[\begin{array}{cccccc} d_1 & 0 & \ldots & 0 \\ 0 & d_2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & d_n \end{array}\right]$

子图的大小

定义一：子集内顶点的个数，记为 $∣ A ∣$
定义二：子集内所有顶点的度之和，记为 $\operatorname{vol}(A):=\sum_{v_i \in A} d_i$

图拉普拉斯矩阵

即：
$L = D - W$

对于任意的向量 $\boldsymbol{f} \in R^n$ 满足：

$\begin{aligned} \boldsymbol{f}^T L \boldsymbol{f} &=\boldsymbol{f}^T(D-W) \boldsymbol{f} =\boldsymbol{f}^T D \boldsymbol{f}-\boldsymbol{f}^T W \boldsymbol{f} \\ &=\sum_{i=1}^n d_i f_i^2-\sum_{i, j=1}^n w_{i j} f_i f_j \\ &=\frac{1}{2}\left(\sum_{i=1}^n d_i f_i^2-2 \sum_{i, j=1}^n w_{i j} f_i f_j+\sum_{j=1}^n d_j f_j^2\right) \\ &=\frac{1}{2}\left(\sum_{i, j=1}^n w_{i j} f_i^2-2 \sum_{i, j=1}^n w_{i j} f_i f_j+\sum_{i, j=1}^n w_{i j} f_j^2\right) \\ &=\frac{1}{2} \sum_{i, j=1}^n w_{i j}\left(f_i^2-2 f_i f_j+f_j^2\right) \\ &=\frac{1}{2} \sum_{i, j=1}^n w_{i j}\left(f_i-f_j\right)^2 \end{aligned}$

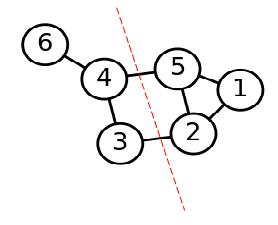
切图

把点集分类在谱聚类算法中的本质就是将无向图切割成几个互不相交的顶点集合，每个顶点集合为： $A_1,A_2,\dots,A_k$ ，它们满足 $A_i \cap A_j=\emptyset$ ， $A_1 \cup A_2 \cup \ldots \cup A_k=V$ .

对于图的两个顶点集合 $A$ 和 $B$ ，两顶点集合之间所有边权重之和使用如下公式表示：
$B):=\sum_{\boldsymbol{v}_i \in A, \boldsymbol{v}_j \in B} w_{i j}$

对于 $k$ 个子图的切分，定义定义切图(我们优化的目标函数)为：

$\operatorname{cut}\left(A_1, A_2, \ldots, A_k\right):=\frac{1}{2} \sum_{i=1}^k W\left(A_i, \bar{A}_i\right)$

其中 $\bar{A}_i$ 为 $A_i$ 的补集，因此想法非常简单，你子集和补集之间联系越低，就越应该被分成两类，就是被切一刀，找到最容易动刀子的几个地方将顶点集合切割成 $k$ 份就实现了分类。

但是，最小化切割可能会导致出现下图这样某些类顶点数量过少的情况，因此我们需要将顶点数量等信息加入考虑：

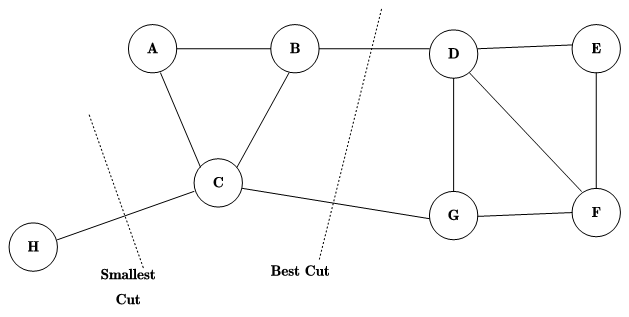
RatioCut切图与Ncut切图

RatioCut切图为了避免第五节的最小切图，对每个切图，不光考虑最小化 $\operatorname{cut}\left(A_1, A_2, \ldots, A_k\right)$ ，它还同时考虑最大化每个子图点的个数，即：
$\operatorname{RatioCut}\left(A_1, A_2, \ldots A_k\right)=\frac{1}{2} \sum_{i=1}^k \frac{W\left(A_i, \bar{A}_i\right)}{\left|A_i\right|}$

而Ncut切图和RatioCut切图很类似，但是把Ratiocut的分母 $\left|A_i\right|$ 换为 $\operatorname{vol}\left(A_i\right)$ ：
$\operatorname{NCut}\left(A_1, A_2, \ldots A_k\right)=\frac{1}{2} \sum_{i=1}^k \frac{W\left(A_i, \bar{A}_i\right)}{\operatorname{vol}\left(A_i\right)}$

由于子图样本的个数多并不一定权重就大，我们切图时基于权重也更合我们的目标，因此一般来说Ncut切图优于RatioCut切图。为了显示篇幅只讲最常用的方法，本文只讲解Ncut切图(RatioCut切图可以非常简单的类比过去)：

我们引入指示向量： $h_j \in\left\{h_1, h_2, \ldots h_k\right\} ,j=1,2, \ldots k$ 对于任意一个向量 $h_j$ , 它是一个n维向量（n为样本数），我们定义 $h_{ij}$ 为：

$h_{i j}= \begin{cases}0 & v_i \notin A_j \\ \frac{1}{\sqrt{v o l\left(A_j\right)}} & v_i \in A_j\end{cases}$

然后我们得把切图用矩阵表示出来，不然一个一个顶点算费老鼻子劲了，有一些大佬就发现，可以用 $h_i^T L h_i$ 表示某个集合的切图：

$\begin{aligned} h_i^T L h_i &=\frac{1}{2} \sum_{m=1} \sum_{n=1} w_{m n}\left(h_{i m}-h_{i n}\right)^2 \\ &=\frac{1}{2}\left(\sum_{m \in A_i, n \notin A_i} w_{m n}\left(\frac{1}{\sqrt{v o l}\left(A_i\right)}-0\right)^2+\sum_{m \notin A_i, n \in A_i} w_{m n}\left(0-\frac{1}{\sqrt{v o l\left(A_i\right)}}\right)^2\right.\\ &=\frac{1}{2}\left(\sum_{m \in A_i, n \notin A_i} w_{m n} \frac{1}{\operatorname{vol}\left(A_i\right)}+\sum_{m \notin A_i, n \in A_i} w_{m n} \frac{1}{\operatorname{vol}\left(A_i\right)}\right.\\ &=\frac{1}{2}\left(\operatorname{cut}\left(A_i, \bar{A}_i\right) \frac{1}{\operatorname{vol}\left(A_i\right)}+\operatorname{cut}\left(\bar{A}_i, A_i\right) \frac{1}{\operatorname{vol}\left(A_i\right)}\right) \\ &=\frac{\operatorname{cut}\left(A_i, \bar{A}_i\right)}{\operatorname{vol}\left(A_i\right)} \end{aligned}$

那么所有子集切图和：
$\operatorname{NCut}\left(A_1, A_2, \ldots A_k\right)=\sum_{i=1}^k h_i^T L h_i=\sum_{i=1}^k\left(H^T L H\right)_{i i}=\operatorname{tr}\left(H^T L H\right)$

最理想的情况下 $h_i$ 应该是单位向量，主要各个软件求特征向量都是求的单位向量，再如果不统一的话某一列特征向量元素值都巨大的话，那很多顶点都会被归为那一类，不过此时 $H^T D H\neq I$ 不是正交的，反而 $H^T D H=I$ ：
$h_i^T D h_i=\sum_{j=1}^n h_{i j}^2 d_j=\frac{1}{\operatorname{vol}\left(A_i\right)} \sum_{j \in A_i} d_j=\frac{1}{\operatorname{vol}\left(A_i\right)} \operatorname{vol}\left(A_i\right)=1$
而若令 $H=D^{-1 / 2} F$ 则：
$H^T L H=F^T D^{-1 / 2} L D^{-1 / 2} F, H^T D H=F^T F=I$
因此优化目标由：
$\underbrace{\arg \min }_H \operatorname{tr}\left(H^T L H\right) \text { s.t. } H^T D H=I$
变为：
$\underbrace{\arg \min }_F \operatorname{tr}\left(F^T D^{-1 / 2} L D^{-1 / 2} F\right) \text { s.t. } F^T F=I$
由于矩阵的迹等于全部特征值之和，我们只需要找到k个最小的特征值并找到其相对应的指示向量。

特征向量聚类

毕竟不是把数据每个点分成一类，而且只要前k个最小特征向量略去了很多信息，因此得到的指示向量不可能像下面这么完美：

0 0 c1
0 0 c1
0 0 c1
c2 0 0
0 c3 0
0 c3 0
… … …

他肯定大体是像这样:

0.1 0.2 0.9
0.0 0.1 0.8
2.0 0.8 0.1
1.8 0.6 0.1
… … …

那简单啊我们直接把行向量当作每一个元素直接k-means一下聚下类就好了呀。完美解决。

MATLAB实现

算法流程

构建样本的相似矩阵 $S$
根据相似矩阵 $S$ 构建邻接矩阵 $W$ ，构建度矩阵 $D$
计算出拉普拉斯矩阵 $L$
标准化的拉普拉斯矩阵 $D^{−1/2}LD^{−1/2}$
计算 $D^{−1/2}LD^{−1/2}$ 最小的k个特征值所各自对应的特征向量 $\boldsymbol{f}$
将各自对应的特征向量 $\boldsymbol{f}$ 组成的矩阵按行标准化，最终组成 $n \times k$ 维的特征矩阵 $F$
对 $F$ 中的每一行作为一个 $k$ 维的样本，共 $n$ 个样本，进行聚类
得到簇划分 $C_1, C_2, \ldots, C_k$

谱聚类函数代码

function C=spectralCluster(X,K,Sigma)
format long;warning off
% 各维度数据归一化
X=X./max(abs(X),[],1:ndims(X));% 计算相似矩阵即||x_i-x_j||^2
S=pdist2(X,X).^2;% 高斯核函数RBF计算邻接矩阵
W=exp(-S./(2.*Sigma.*Sigma));% 计算度矩阵
D=diag(sum(W,2));% 计算拉普拉斯矩阵
L=D-W;
L_norm=D^(-1/2)*L*D^(-1/2);% 求特征向量 V
% 'SM':绝对值最小特征值排列
[V, ~]=eigs(L_norm,K,'SM');% 按行标准化
V_norm=V./vecnorm(V.')';% 对特征向量合并矩阵的行向量求k-means
C=kmeans(V_norm,K);
end

示例一：凸散点

% 随机数据生成
PntSet1=mvnrnd([2 3],[1 0;0 2],500);
PntSet2=mvnrnd([3 4],[1 0;0 2],500);
PntSet3=mvnrnd([8 2],[1 0;0 1],500);
X=[PntSet1;PntSet2;PntSet3];% 谱聚类
figure(1)
K=3;
Sigma=1;
C=spectralCluster(X,K,Sigma);
hold on
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end
legend% 传统k-means
figure(2)
C=kmeans(X,K);
hold on 
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end

与k-means聚类效果相似，上图为谱聚类，下图为传统k-means：

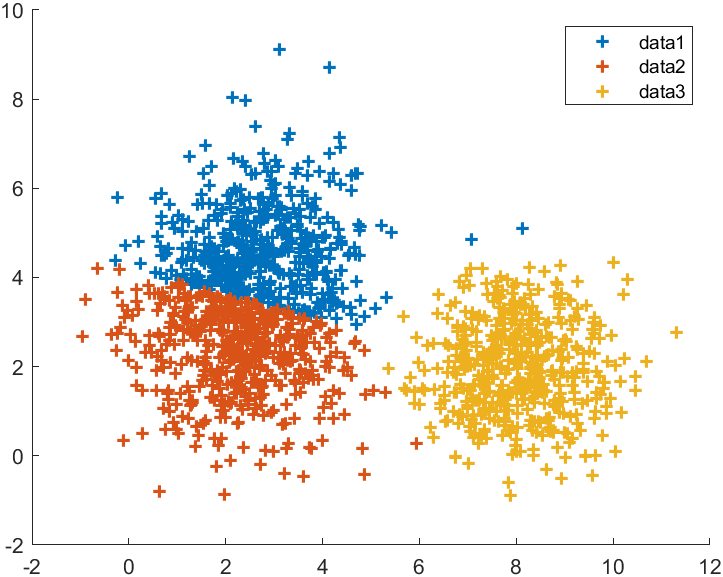
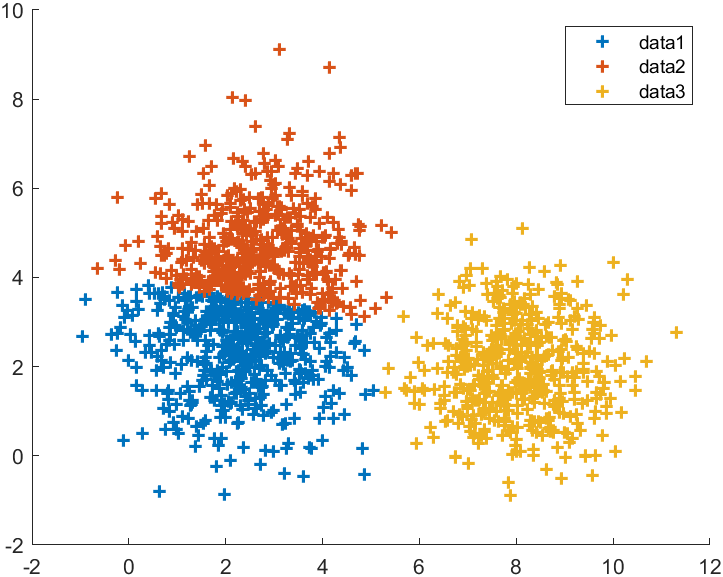
示例二：双圆

% 随机数据生成
t=linspace(0,2*pi,100)';
PntSet1=[cos(t),sin(t)].*[2.1,2.5]+rand([100,2]);
PntSet2=[cos(t),sin(t)].*[10.5,12.6]+rand([100,2]);
X=[PntSet1;PntSet2];% 谱聚类
figure(1)
K=2;
Sigma=.1;
C=spectralCluster(X,K,Sigma);
hold on
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end
legend% 传统k-means
figure(2)
C=kmeans(X,K);
hold on 
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end 
legend

上图为谱聚类，下图为传统k-means：

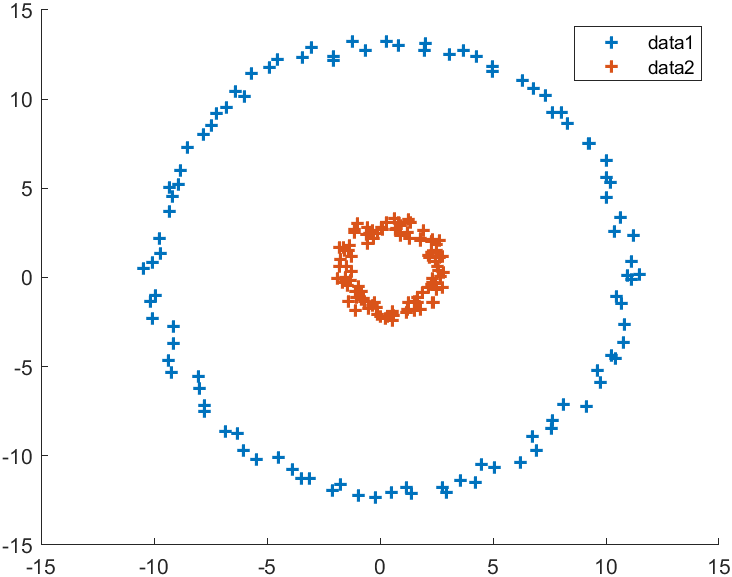
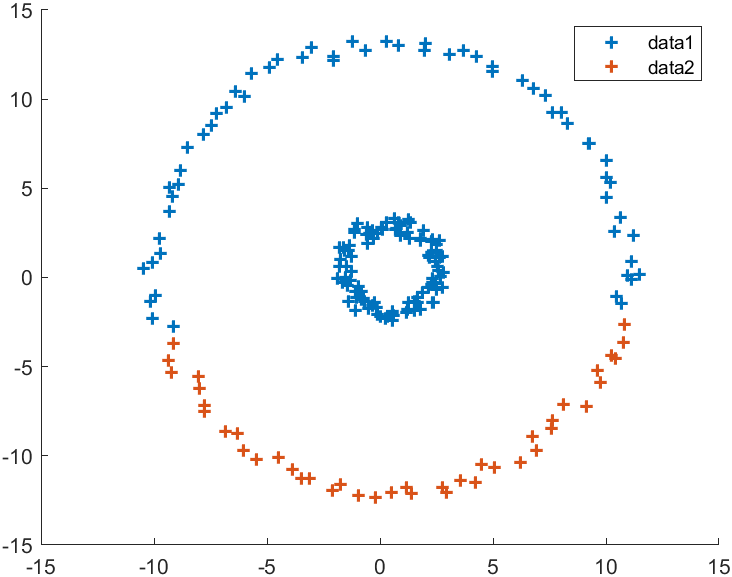
示例三：slandarer

X=load('slandarer.mat');
X=X.X;% 谱聚类
K=9;
Sigma=.02;
C=spectralCluster(X,K,Sigma);
hold on
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end
legend% 传统k-means
figure(2)
C=kmeans(X,K);
hold on 
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end 
legend

数据源自文末压缩包内slandarer.mat，上图为谱聚类，下图为传统k-means：

示例四：双弧

X=load('arcs2.mat');
X=X.X;% 谱聚类
figure(1)
K=2;
Sigma=.05;
C=spectralCluster(X,K,Sigma);
hold on 
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end 
legend% 传统k-means
figure(2)
C=kmeans(X,K);
hold on 
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end 
legend

数据源自文末压缩包内arcs2.mat，上图为谱聚类，下图为传统k-means：

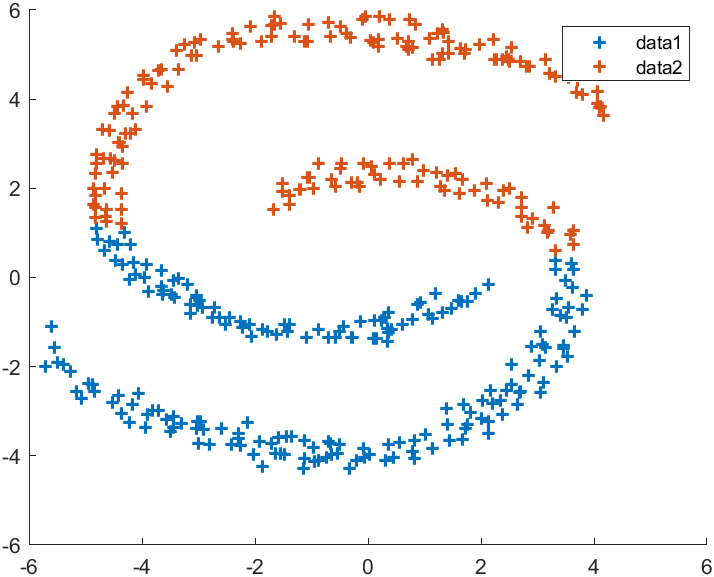
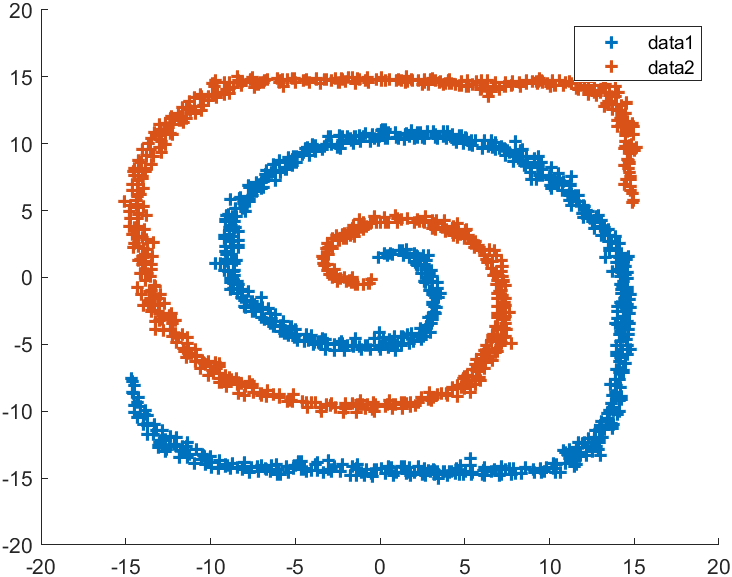
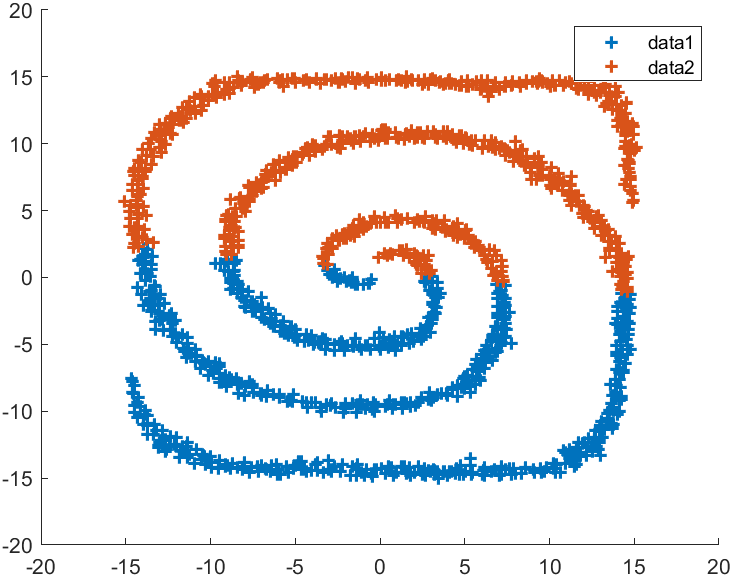
示例五：双螺旋

X=load('screw.mat');
X=X.X;% 谱聚类
figure(1)
K=2;
Sigma=.02;
C=spectralCluster(X,K,Sigma);
hold on 
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end 
legend% 传统k-means
figure(2)
C=kmeans(X,K);
hold on 
for i=1:Kplot(X(C==i,1),X(C==i,2),'+','LineWidth',1.5)
end 
legend