文章目录
- 简介
- 距离矩阵
- 最短距离法
- 最长距离法
- 类平均法
- 重心法
- python应用
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。
简介
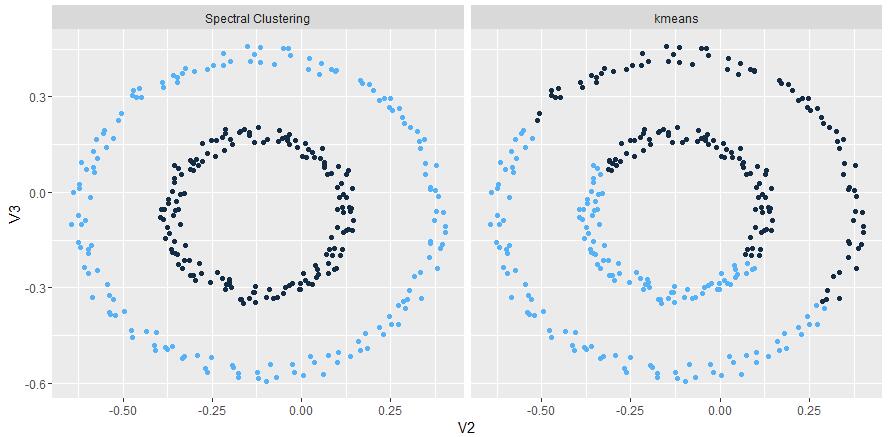
层次聚类(Hierarchical Clustreing)又称谱系聚类,通过在不同层次上对数据集进行划分,形成树形的聚类结构。很好体现类的层次关系,且不用预先制定聚类数,对大样本也有较好效果。
算法步骤:
- 计算类间距离矩阵
- 初始化n个类,将每个样本视为一类
- 在距离矩阵中选择最小的距离,合并这两个类为新类
- 计算新类到其他类的距离,得到新的距离矩阵
- 重复3-4步,直至最后合并为一个类
首先介绍距离矩阵的计算,然后第4步有不同的算法来定义新类到其他类的距离,包括:最短距离法、最长距离法、类平均法、重心法等。
距离矩阵
使用距离来作为样品间的相似性度量,往往常用欧氏距离。
比如给定数据:
| x1 | x2 | x3 |
|---|---|---|
| 2 | 4 | 7 |
| 5 | 8 | 7 |
| 4 | 6 | 6 |
该数据包含特征x1、x2和x3,第一个样品[2,4,7],第二个样品[5,8,7],第三个样品[4,6,6],将每个样品各看作一类, G i = { i } , i = 1 , 2 , 3 , 4 G_i=\{i\},i=1,2,3,4 Gi={i},i=1,2,3,4。
根据欧式距离:
d ( x i , x j ) = [ ∑ k = 1 p ( x i k − x j k ) 2 ] 1 2 d(x_i,x_j)=[\sum^p_{k=1}(x_{ik}-x_{jk})^2]^{\frac{1}{2}} d(xi,xj)=[k=1∑p(xik−xjk)2]21
D 12 = D 21 = ( 2 − 5 ) 2 + ( 4 − 8 ) 2 + ( 7 − 7 ) 2 = 5 D_{12}=D_{21}=\sqrt{(2-5)^2+(4-8)^2+(7-7)^2}=5 D12=D21=(2−5)2+(4−8)2+(7−7)2=5
D 13 = D 31 = ( 2 − 4 ) 2 + ( 4 − 6 ) 2 + ( 7 − 6 ) 2 = 3 D_{13}=D_{31}=\sqrt{(2-4)^2+(4-6)^2+(7-6)^2}=3 D13=D31=(2−4)2+(4−6)2+(7−6)2=3
D 23 = D 32 = ( 5 − 4 ) 2 + ( 8 − 6 ) 2 + ( 7 − 6 ) 2 = 6 ≈ 2.5 D_{23}=D_{32}=\sqrt{(5-4)^2+(8-6)^2+(7-6)^2}=\sqrt{6}≈2.5 D23=D32=(5−4)2+(8−6)2+(7−6)2=6≈2.5
也就是距离矩阵D为:
| G 1 G_1 G1 | G 2 G_2 G2 | G 3 G_3 G3 | |
|---|---|---|---|
| G 1 G_1 G1 | 0 | ||
| G 2 G_2 G2 | 5 | 0 | |
| G 3 G_3 G3 | 3 | 2.5 | 0 |
由于是对称矩阵,给出下三角即可。
除了欧式距离,也可使用其他距离公式。或者使用相关系数来度量,越接近1表示越相关,计算相关系数矩阵。
最短距离法
设类 G r G_r Gr由 G p , G q G_p,G_q Gp,Gq合并得来,包含 n r = n p + n q n_r=n_p+n_q nr=np+nq个样品,最短距离法:
D r k = m i n { D p d , D q k } D_{rk}=min\{D_{pd},D_{qk}\} Drk=min{Dpd,Dqk}
在上述矩阵 D D D中, D 23 = 2.5 D_{23}=2.5 D23=2.5最小,也就是合并 G 2 G_2 G2和 G 3 G_3 G3为新类 G 4 = { 2 , 3 } G_4=\{2,3\} G4={2,3}
用最短距离法,计算新类到其他类距离:
D 41 = m i n { D 21 , D 3 , 1 } = m i n { 5 , 3 } = 3 D_{41}=min\{D_{21},D_{3,1}\}=min\{5,3\}=3 D41=min{D21,D3,1}=min{5,3}=3
得到新的距离矩阵D’为:
| G 1 G_1 G1 | G 4 G_4 G4 | |
|---|---|---|
| G 1 G_1 G1 | 0 | |
| G 4 G_4 G4 | 3 | 0 |
重复上述步骤,在D’中合并取 D 14 = 3 D_{14}=3 D14=3最小,合并类 G 1 G_1 G1和 G 4 G_4 G4为新类,此时只有一个类,流程结束。
根据上述步骤绘制谱系图,横坐标就是每个类,纵坐标表示合并两个类时的值:
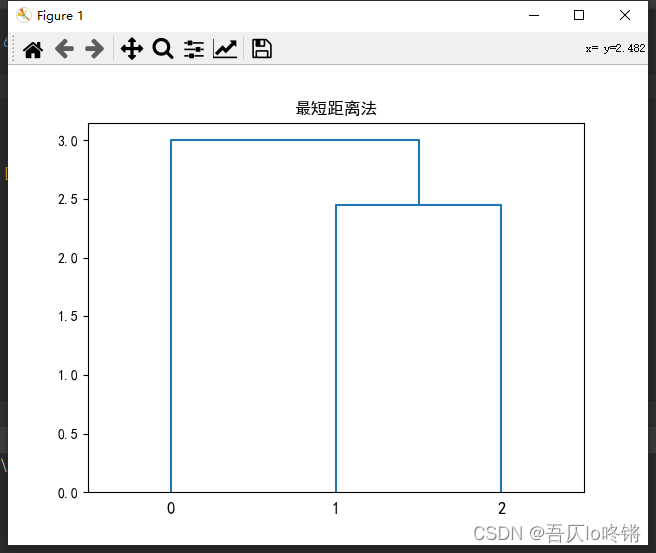
根据谱系图,如果要聚类为2类,从上往下看首次出现了2个分支的地方,即将样品0分为一类,样品1、2分为另一类。
最长距离法
设类 G r G_r Gr由 G p , G q G_p,G_q Gp,Gq合并得来,包含 n r = n p + n q n_r=n_p+n_q nr=np+nq个样品,最长距离法:
D r k = m a x { D p d , D q k } D_{rk}=max\{D_{pd},D_{qk}\} Drk=max{Dpd,Dqk}
在上述矩阵 D D D中, D 23 = 2.5 D_{23}=2.5 D23=2.5最小,也就是合并 G 2 G_2 G2和 G 3 G_3 G3为新类 G 4 = { 2 , 3 } G_4=\{2,3\} G4={2,3}
用最长距离法,计算新类到其他类距离:
D 41 = m a x { D 21 , D 3 , 1 } = m i n { 5 } = 5 D_{41}=max\{D_{21},D_{3,1}\}=min\{5\}=5 D41=max{D21,D3,1}=min{5}=5
得到新的距离矩阵D’为:
| G 1 G_1 G1 | G 4 G_4 G4 | |
|---|---|---|
| G 1 G_1 G1 | 0 | |
| G 4 G_4 G4 | 5 | 0 |
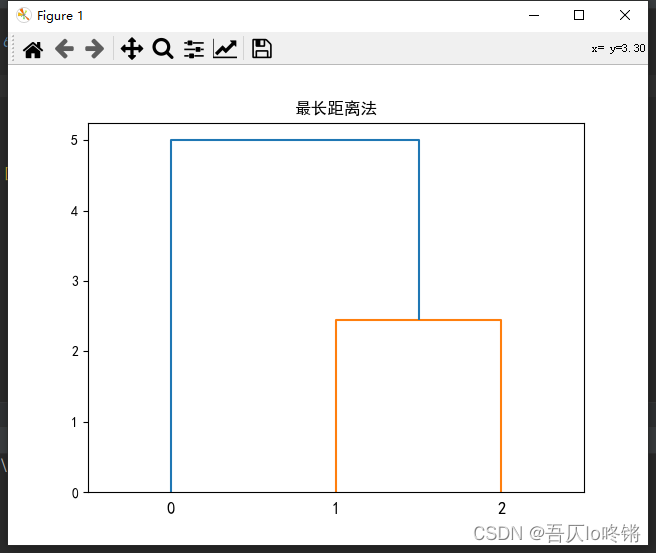
重复上述步骤,在D’中合并取 D 14 = 5 D_{14}=5 D14=5最小,合并类 G 1 G_1 G1和 G 4 G_4 G4为新类,此时只有一个类,流程结束。
得到谱系图如下:
类平均法
设类 G r G_r Gr由 G p , G q G_p,G_q Gp,Gq合并得来,包含 n r = n p + n q n_r=n_p+n_q nr=np+nq个样品,类平均法:
D r k = n p n r D p k + n q n r D q k D_{rk}=\frac{n_p}{n_r}D_{pk}+\frac{n_q}{n_r}D_{qk} Drk=nrnpDpk+nrnqDqk
在上述矩阵 D D D中, D 23 = 2.5 D_{23}=2.5 D23=2.5最小,也就是合并 G 2 G_2 G2和 G 3 G_3 G3为新类 G 4 = { 2 , 3 } G_4=\{2,3\} G4={2,3}
用类平均法,计算新类到其他类距离:
D 41 = 1 2 × 5 + 1 2 × 3 = 4 D_{41}=\frac{1}{2}×5+\frac{1}{2}×3=4 D41=21×5+21×3=4
得到新的距离矩阵D’为:
| G 1 G_1 G1 | G 4 G_4 G4 | |
|---|---|---|
| G 1 G_1 G1 | 0 | |
| G 4 G_4 G4 | 4 | 0 |
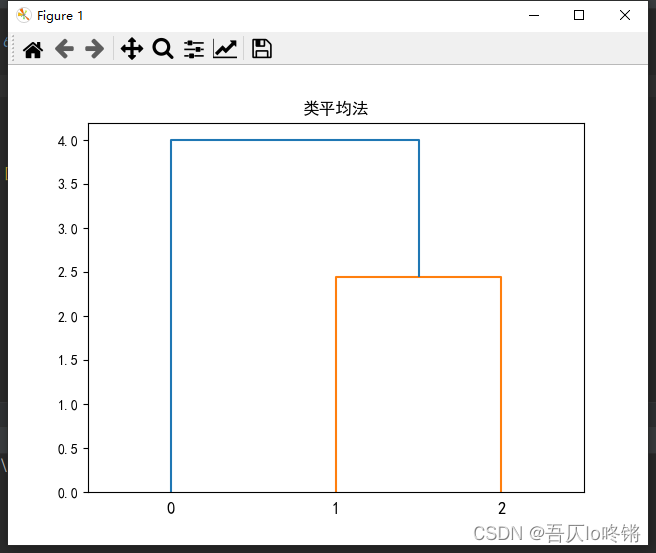
重复上述步骤,在D’中合并取 D 14 = 4 D_{14}=4 D14=4最小,合并类 G 1 G_1 G1和 G 4 G_4 G4为新类,此时只有一个类,流程结束。
得到谱系图如下:
(
插播反爬信息)博主CSDN地址:https://wzlodq.blog.csdn.net/
重心法
设类 G r G_r Gr由 G p , G q G_p,G_q Gp,Gq合并得来,包含 n r = n p + n q n_r=n_p+n_q nr=np+nq个样品,重心法:
D r k = [ n p n r D p k 2 + n q n r D q k 2 − n p n r n q n r D p q 2 ] 1 2 D_{rk}=[\frac{n_p}{n_r}D_{pk}^2+\frac{n_q}{n_r}D_{qk}^2-\frac{n_p}{n_r}\frac{n_q}{n_r}D_{pq}^2]^{\frac{1}{2}} Drk=[nrnpDpk2+nrnqDqk2−nrnpnrnqDpq2]21
在上述矩阵 D D D中, D 23 = 2.5 D_{23}=2.5 D23=2.5最小,也就是合并 G 2 G_2 G2和 G 3 G_3 G3为新类 G 4 = { 2 , 3 } G_4=\{2,3\} G4={2,3}
用重心法,计算新类到其他类距离:
D 41 = [ 1 2 5 2 + 1 2 3 2 − 1 2 1 2 6 2 ] 1 2 = 15.5 ≈ 3.9 D_{41}=[\frac{1}{2}5^2+\frac{1}{2}3^2-\frac{1}{2}\frac{1}{2}\sqrt{6}^2]^{\frac{1}{2}}=\sqrt{15.5}≈3.9 D41=[2152+2132−212162]21=15.5≈3.9
得到新的距离矩阵D’为:
| G 1 G_1 G1 | G 4 G_4 G4 | |
|---|---|---|
| G 1 G_1 G1 | 0 | |
| G 4 G_4 G4 | 3.9 | 0 |
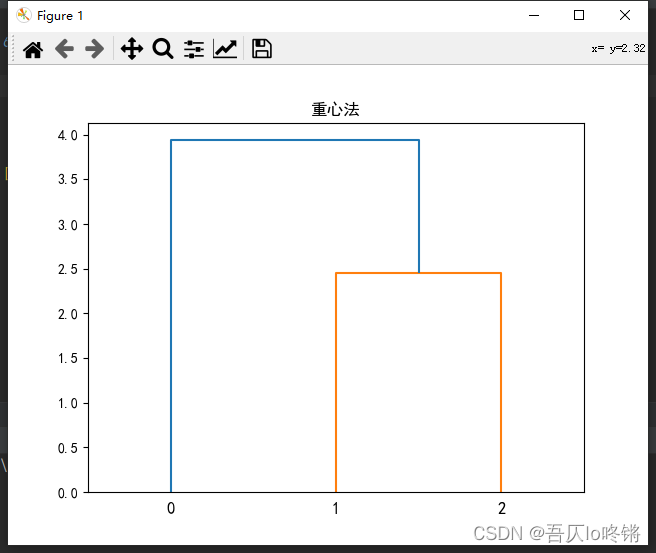
重复上述步骤,在D’中合并取 D 14 = 3.9 D_{14}=3.9 D14=3.9最小,合并类 G 1 G_1 G1和 G 4 G_4 G4为新类,此时只有一个类,流程结束。
得到谱系图如下:
python应用
- 使用scipy库中的
linkage函数
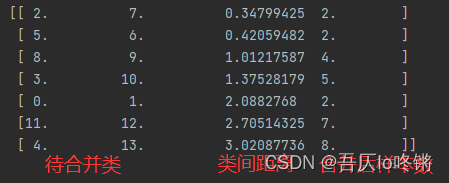
linkage(y, method=‘single’, metric=‘euclidean’)
method取值single表示最短距离法、complete最长距离法、average类平均法、centroid重心法。
import pandas as pd
from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkagedata = [[76.1, 74.33, 78.01],[74.91, 73.31, 76.63],[72.54, 70.68, 74.57],[71.65, 69.96, 73.57],[69.87, 68.29, 71.79],[73.34, 71.51, 75.36],[73.1, 71.38, 75.04],[72.37, 70.39, 74.66]]
data = pd.DataFrame(data, columns=['X1', 'X2', 'X3'],index=['北京', '天津', '河北', '山西', '内蒙古', '辽宁', '吉林', '黑龙江'])
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.figure(figsize=(6, 5))
# 用最短距离法
plt.subplot(2, 2, 1)
plt.tight_layout(pad=2.5)
plt.title('最短距离法')
z1 = linkage(data, 'single')
dendrogram(z1)# 用最长距离法
plt.subplot(2, 2, 2)
plt.title('最长距离法')
z2 = linkage(data, 'complete')
dendrogram(z2)# 用类平均法
plt.subplot(2, 2, 3)
plt.title('类平均法')
z3 = linkage(data, 'average')
dendrogram(z3)# 用重心法
plt.subplot(2, 2, 4)
plt.title('重心法')
z4 = linkage(data, 'centroid')
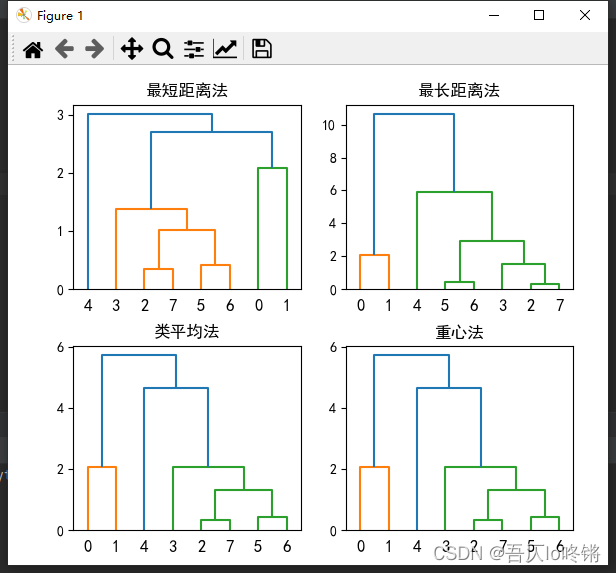
dendrogram(z4)
plt.show()
- 使用sklearn库中的
AgglomerativeClustering函数
使用linkage参数定义合并算法。
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from scipy.cluster.hierarchy import dendrogram
from sklearn.cluster import AgglomerativeClusteringdef plot_dendrogram(model, **kwargs): # 可视化counts = np.zeros(model.children_.shape[0])n_samples = len(model.labels_)for i, merge in enumerate(model.children_):current_count = 0for child_idx in merge:if child_idx < n_samples:current_count += 1else:current_count += counts[child_idx - n_samples]counts[i] = current_countlinkage_matrix = np.column_stack([model.children_, model.distances_, counts]).astype(float)dendrogram(linkage_matrix, **kwargs)data = [[76.1, 74.33, 78.01],[74.91, 73.31, 76.63],[72.54, 70.68, 74.57],[71.65, 69.96, 73.57],[69.87, 68.29, 71.79],[73.34, 71.51, 75.36],[73.1, 71.38, 75.04],[72.37, 70.39, 74.66]]
data = pd.DataFrame(data, columns=['X1', 'X2', 'X3'],index=['北京', '天津', '河北', '山西', '内蒙古', '辽宁', '吉林', '黑龙江'])plt.rcParams['font.sans-serif'] = ['SimHei']
plt.figure(figsize=(6, 5))
# 用最短距离法
plt.subplot(2, 2, 1)
plt.tight_layout(pad=2.5)
plt.title('最短距离法')
model1 = AgglomerativeClustering(linkage='single', distance_threshold=0, n_clusters=None)
model1.fit(data)
plot_dendrogram(model1)
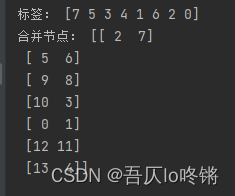
print("标签:", model1.labels_)
print("合并节点:", model1.children_)# 用最长距离法
plt.subplot(2, 2, 2)
plt.title('最长距离法')
model2 = AgglomerativeClustering(linkage='complete', distance_threshold=0, n_clusters=None)
model2.fit(data)
plot_dendrogram(model2)# 用类平均法
plt.subplot(2, 2, 3)
plt.title('类平均法')
model3 = AgglomerativeClustering(linkage='average', distance_threshold=0, n_clusters=None)
model3.fit(data)
plot_dendrogram(model3)# 用重心法
plt.subplot(2, 2, 4)
plt.title('重心法')
model4 = AgglomerativeClustering(linkage='ward', distance_threshold=0, n_clusters=None)
model4.fit(data)
plot_dendrogram(model4)
plt.show()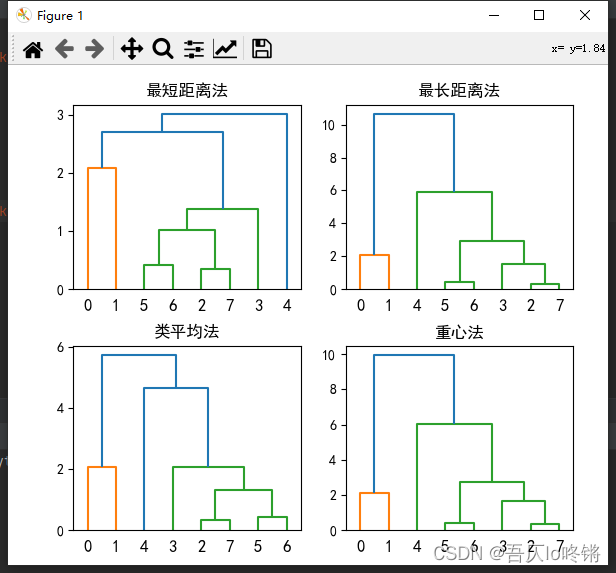
原创不易,请勿转载(
本不富裕的访问量雪上加霜)
博主首页:https://wzlodq.blog.csdn.net/
来都来了,不评论两句吗👀
如果文章对你有帮助,记得一键三连❤