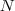目录

1 背景

2 单位根

3 单位根检验

4 ADF检验

5 python 实现与结果解释

---

1 背景

        在使用很多时间序列模型的时候，如 ARMA、ARIMA，都会要求时间序列是平稳的，所以一般在研究一段时间序列的时候，第一步都需要进行平稳性检验，除了用肉眼检测的方法，另外比较常用的严格的统计检验方法就是ADF检验，也叫做单位根检验。

        ADF检验全称是 Augmented Dickey-Fuller test，顾名思义，ADF是 Dickey-Fuller检验的增广形式。DF检验只能应用于一阶情况，当序列存在高阶的滞后相关时，可以使用ADF检验，所以说ADF是对DF检验的扩展。

        ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。

2 单位根

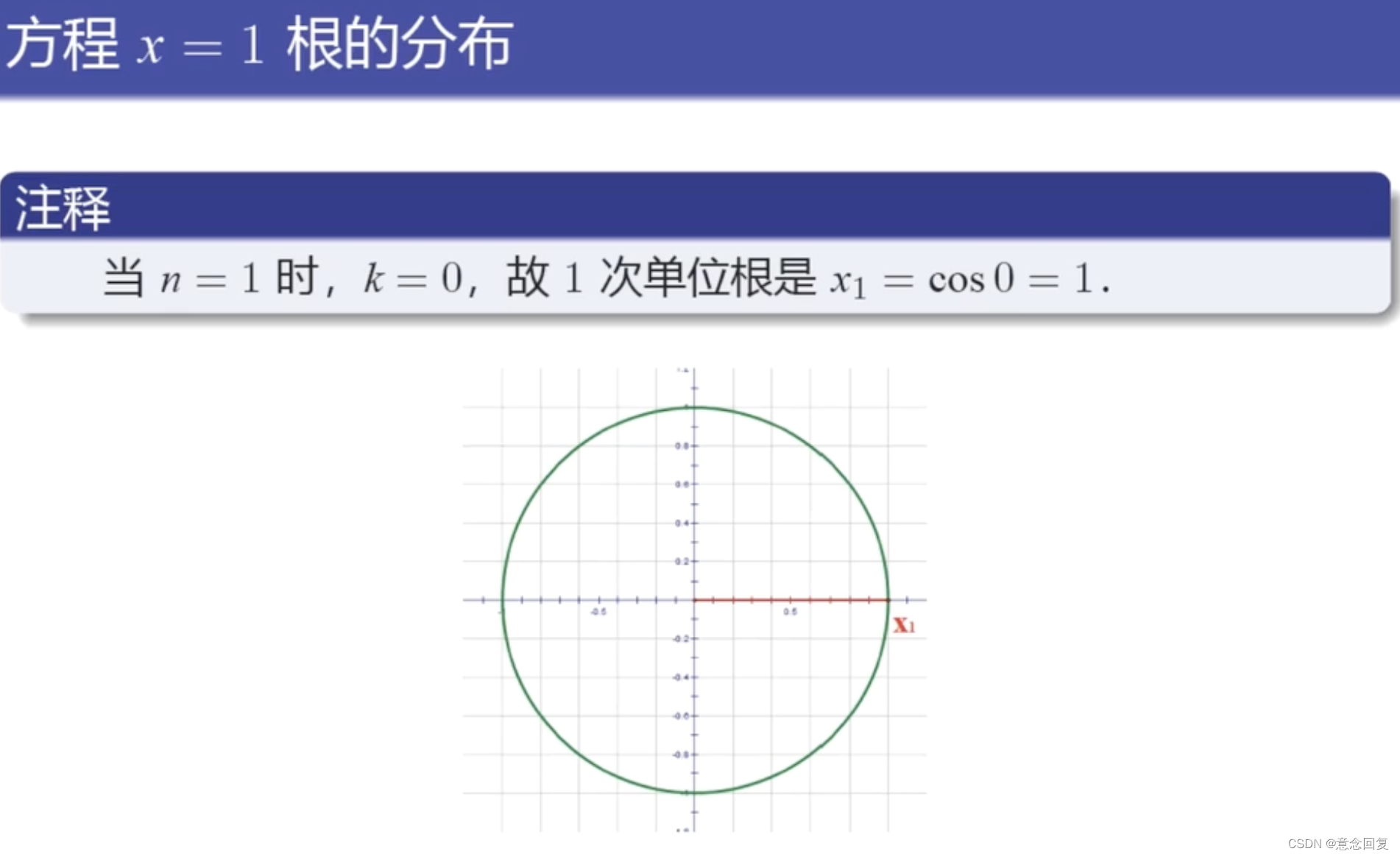
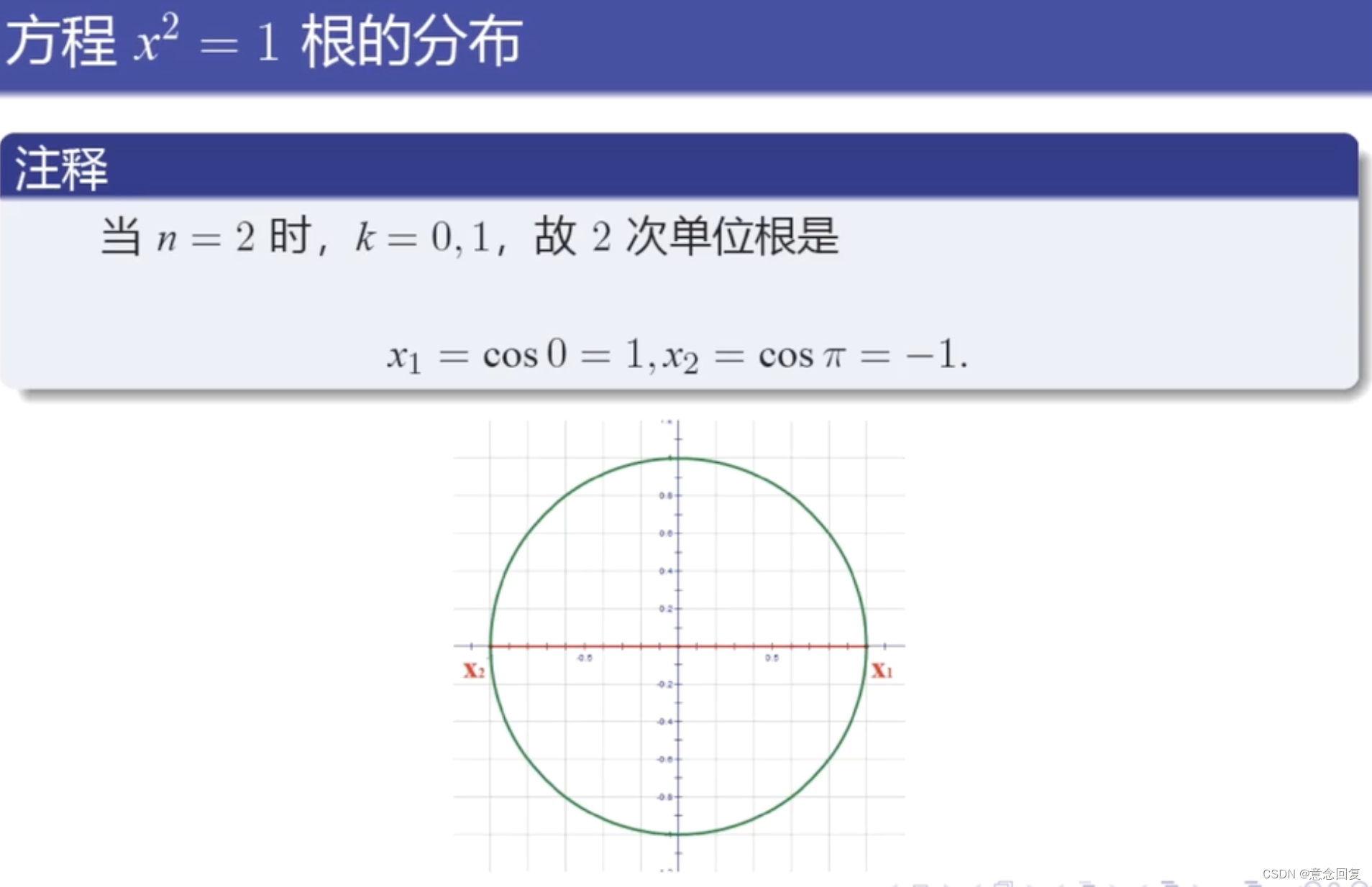
        数学上，n次单位根是n次幂为1的复数。它们位于复平面的单位圆上，构成正n边形的顶点，其中一个顶点是1。

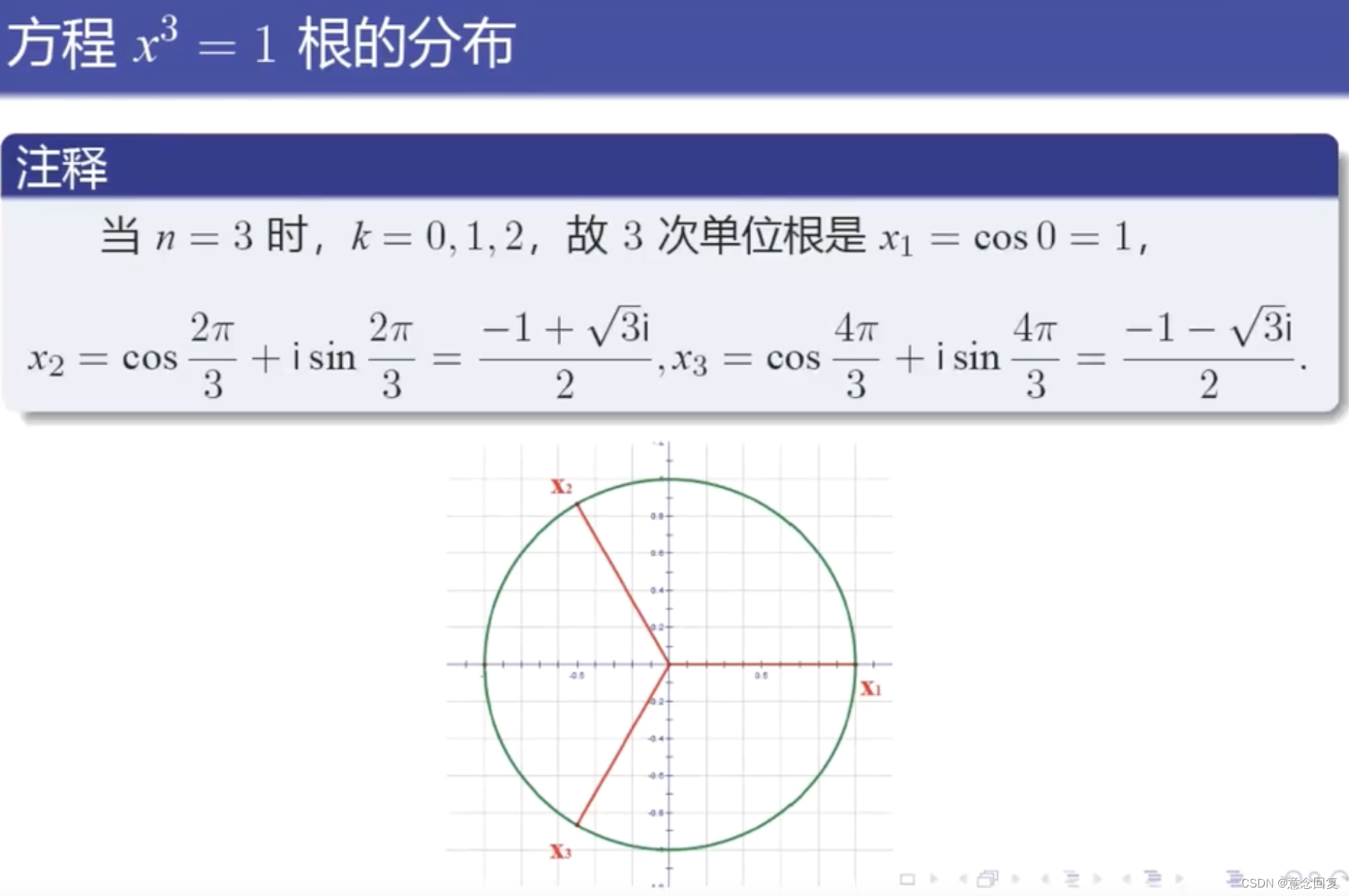
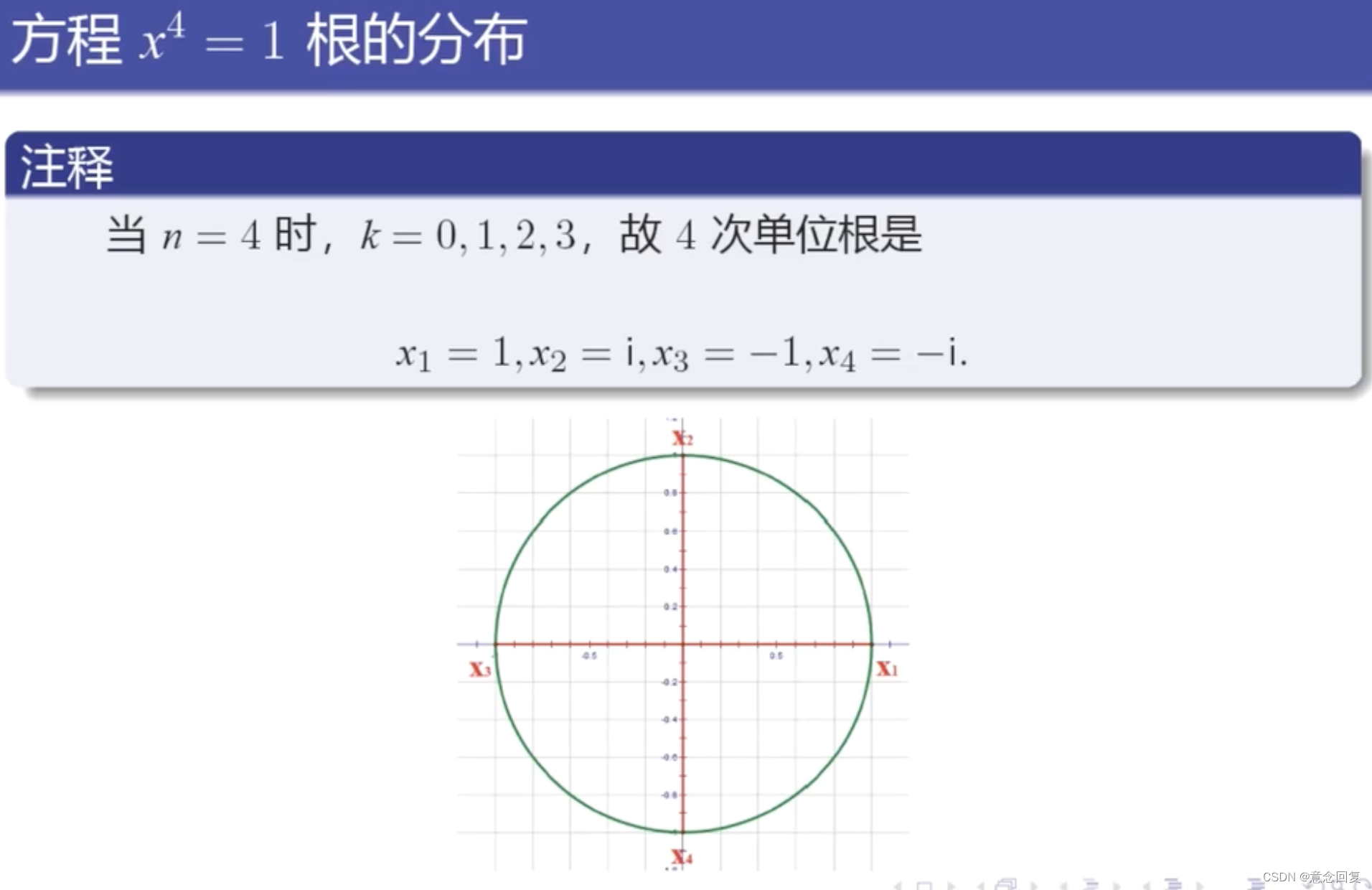
3 单位根检验

        先来看一阶AR模型，即AR(1)的情况，其模型如下：

             

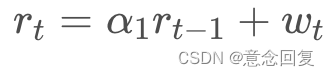
• 如果 ，该模型就是随机游走，我们知道它是不平稳的。换个思路想象一下，当 ，那么前一时刻的收益率对当下时刻的影响是100%的，不会减弱；那么就算是很远的某个时刻，当下对它的影响还是不会消除，所以方差（表现在波动）是受前面所有时刻的影响，是和 t 相关的，因此不平稳；
• 如果 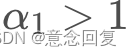，那么当前时刻的波动不仅受前面时刻的影响，还被放大了，所以肯定不平稳；
• 只有当 的时候，前面时刻的波动对当前时刻的影响会逐渐减小。可以计算此时的自协方差以及自相关系数是一个固定值。所以这种情况下，序列是平稳的。

        对于高阶的AR模型也是一样的，一个AR （P）阶 模型如下： 

              

        如果 都小于1，那么这个序列是平稳的；存在某一个 ，这个序列就不是平稳的。

        要判断 是否都小于1，一般利用AR模型的特征方程，如下：

        

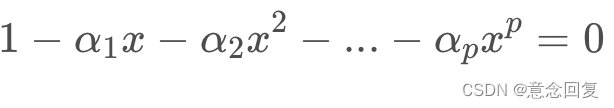
        这个方程有p个根。

       检验AR序列是否平稳，就是检验是否存在某个根大于等于1。这个过程叫单位根检验。

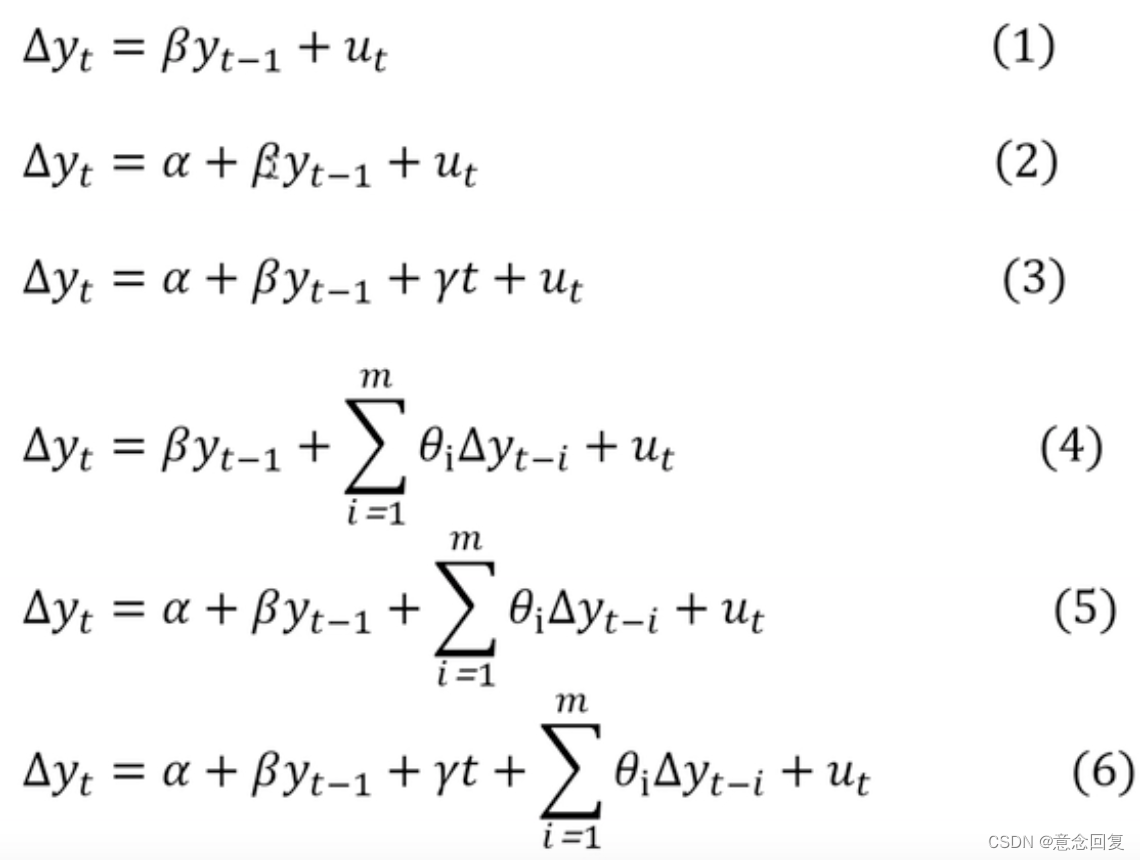
4 ADF检验

        ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。

        所以，ADF检验的

• H0 假设：存在单位根，序列不平稳；
• H1 假设：不存在单位根，序列平稳；

        如果得到的显著性检验统计量小于三个置信度（10%，5%，1%），则对应有（90%，95，99%）的把握来拒绝原假设，即为平稳序列。

5 python 实现与结果解释​​​​​​​

ADF检验：Augmented Dickey–Fuller test 又称为扩展迪基-福勒检验，其可以用来检测当前序列是否平稳。ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。判断序列是否平稳的流程为：

（1）判断p_value值是否小于0.05置信区间（如果p值小于0.05，说明错误拒绝H0的概率很低，则我们有理由相信H0本身就是错误的，而非检验错误导致），若小于0.05，则可以认为拒绝原假设，数据不存在单位根，序列平稳；若大于或等于0.05，则不能显著拒绝原假设，需要进行下一步判断。

（2）进行T检验，如果 T统计量小于10%水平下（90%置信区间）的数字就可以拒绝原假设，认为数据平稳；否则认为数据不平稳。

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller"""
判断是不是平稳数据
https://blog.csdn.net/aaakirito/article/details/116651795
"""
"""
ADF检验的原理
ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。
所以，ADF检验的 H0 假设就是存在单位根，如果得到的显著性检验统计量小于三个置信度（10%，5%，1%），则对应有（90%，95，99%）的把握来拒绝原假设。
"""
# 数据一、周期数据
fs = 100  # frequency: 100  Hz
Fs = 1000 # sampling frequency: 1000 Hz
dt = 1/Fs # sampling period
N = 100
T = N * dt # span
t = np.linspace(0, T, N, endpoint = False) # time
data = np.cos(2 * np.pi * fs * t) + np.random.normal(scale = 0.2, size = len(t))# 数据二、随机数据
# data = np.random.randint(6, 10, 300)plt.plot(data)
plt.show()alpha = 0.05result = adfuller(data)
print((result))
if result[1] < alpha:  # p_value值大，无法拒接原假设,有可能单位根，需要T检验print("stationarity")
else:if result[0] < result[4]['5%']:  # 代表t检验的值小于5%,置信度为95%以上，这里还有'1%'和'10%'print("stationarity")  # 拒接原假设，无单位根，平稳的else:print("no_stationarity")  # 无法拒绝原假设，有单位根，不平稳的# 结果解释
# 第一个是adt检验的结果，简称为T值，表示t统计量。
# 第二个简称为p值，表示t统计量对应的概率值。
# 第三个表示延迟。
# 第四个表示测试的次数。
# 第五个是配合第一个一起看的，是在99%，95%，90%置信区间下的临界的ADF检验的值。# 第一点，1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较，
# ADF Test result（第一个值）同时小于1%、5%、10%即说明非常好地拒绝该假设。本数据中，adf结果为-8， 小于三个level的统计值
# 第二点，p值要求小于给定的显著水平，p值要小于0.05，等于0是最好的。本数据中，P-value 为 1e-15,接近0.
# p值为0.0229<0.05，说明在5%下显著，即拒绝原假设，是平稳的。

 结果：

(-9.078071590100102, 4.127093240000678e-15, 6, 93, {'1%': -3.502704609582561, '5%': -2.8931578098779522, '10%': -2.583636712914788}, 1.7840114490861652)

第一个是adt检验的结果，简称为T值，表示t统计量。
第二个简称为p值，表示t统计量对应的概率值。
第三个表示延迟。
第四个表示测试的次数。
第五个是配合第一个一起看的，是在99%，95%，90%置信区间下的临界的ADF检验的值。

判断是否平稳：

第一点，1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较，ADF Test result（第一个值）同时小于1%、5%、10%即说明非常好地拒绝该假设（即为平稳数据）。本数据中，adf结果为-9.078， 小于三个level的统计值
第二点，p值要求小于给定的显著水平，p值要小于0.05，等于0是最好的。本数据中，P-value 为 1e-15,接近0。p值为4.127e-15<0.05，说明在5%下显著，即拒绝原假设，是平稳的。

检验统计量P值的由来、含义、应用

1 ．P值的由来

        除了利用拒绝域和接受域来判断和抉择是否拒绝原假设以外，我们还可以利用伴随概率进行判断。伴随概率是指当原假设为真时检验统计量取该观察值或更极端值的概率，此概率值我们称为 P值（P-value）。每一个检验统计量都会对应一个P值。P值是用来测量样本观测数据与原假设中假定的μ值的偏离程度。P值越小，说明实际观测到的数据与H 0 之间不一致的程度就越大，检验的结果也就越显著。

2 ．P值的含义

        我们知道显著性水平α是人为选定的，即事先设定犯弃真错误的最大允许概率值；P 值则是构造出的检验统计量落在拒绝域内的概率值，P值是实际计算出来的。P值越小，对于更小的概率值，检验统计量竟然落在了拒绝域，说明拒绝原假设的理由更充分。

3 ．P值的应用

         一般我们将某统计量的观察值对应的P值与设定的显著性水平α进行比较，若P≤α，则我们有更充分的理由拒绝原假设；若 P >α，则我们不能拒绝原假设。常用的统计软件如 EViews、SPSS等的分析结果中均会给出检验统计量对应的P值，因此在实际应用中，我们常用P值作为判断的准则。

检验统计量：检验统计量_百度百科

单位根_哔哩哔哩_bilibili单位根检验、ADF检验、平稳性检验_哔哩哔哩_bilibili单位根_哔哩哔哩_bilibili

浅谈p值（p-value是什么）：https://www.jianshu.com/p/4c9b49878f3d?u_atoken=5e49152f-59df-419b-89ff-d19b18d6d7e1&u_asession=01zxCAr9V_hf86Bi7fxPxaQOWAR5tz30J_eVi-N6mM44D-kdw-6H1jNOofbXRouLjnX0KNBwm7Lovlpxjd_P_q4JsKWYrT3W_NKPr8w6oU7K-NobWTG_xwyXZzPasDVPJ73KmjkU3JT7ddtoHBlecZWGBkFo3NEHBv0PZUm6pbxQU&u_asig=05B84LN60qDaOs1YORDHf9wjzQIfWoaDvgJFwl2uKFbhOKYrcaqSqZ7H8o0zmnRZzSaXxYy1bJwW0myY2mlQ5hsPgarhUtF1ewS6oWXT7MoAAQNJRH-_QMeunebqkSLPtuDJK1Rt-m63DTcBOT2grsGFozBa9wKQ_qJ8ehpf8idGX9JS7q8ZD7Xtz2Ly-b0kmuyAKRFSVJkkdwVUnyHAIJzTcpd4hcOD5-oGCZAD6vpu-rmGTP_3SaRf9MwpqatSbbzKnPGeiYgOeAvNODIGQOu-3h9VXwMyh6PgyDIVSG1W9CsWlR44eK-jlHDID87XwgLrOBOWgTd5WAMvZk50HQNAcrSzr3tpkB_SrSF79k6SD1rDWJx64VZOfVQV3fhMivmWspDxyAEEo4kbsryBKb9Q&u_aref=NHbUuXXuKmWewNuhGq2xhlO9CIw%3D