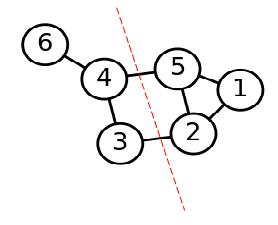
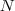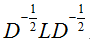谱聚类算法 matlab

1、谱聚类算法步骤公式
（1）整理数据集，使数据集中数据在0-1之间。假设数据集m行n列。
（2）求邻接矩阵W。元素值为每一点到其他点之间距离，即权重。
（3）求相似度矩阵S，相似度矩阵的定义。相似度矩阵由权值矩阵得到，实践中一般用高斯核函数（也称径向基函数核）计算相似度，距离越大，代表其相似度越小。（这里我认为相似度矩阵与邻接矩阵一个概念，邻接矩阵即在图中表示顶点之间相邻关系的矩阵，因此这里用相似度矩阵表示该图顶点之间的相互关系）

（4）求度矩阵D。把的每一列元素加起来得到个数，然后把它们放在对角线上（其它地方都是零），组成一个的对角矩阵，记为度矩阵。
（5）求拉普拉斯矩阵L。使用Normalized相似变换 L=I-D-(1/2)SD-(1/2) (I单位矩阵)
（6）求出L的最小的k个特征值和对应的特征向量V

（7）将特征向量V进行kmeans聚类(少量的特征向量)，得到m行1列的矩阵，即分类结果。

2、谱聚类算法matlab实现
function C = spectral(W,sigma, num_clusters)
% 谱聚类算法
% 使用Normalized相似变换
% 输入  : W              : N-by-N 矩阵, 即连接矩阵
%        sigma          : 高斯核函数,sigma值不能为0
%        num_clusters   : 分类数
%
% 输出  : C : N-by-1矩阵 聚类结果，标签值
%format longm = size(W, 1);%计算相似度矩阵  相似度矩阵由权值矩阵得到，实践中一般用高斯核函数W = W.*W;   %平方W = -W/(2*sigma*sigma);S = full(spfun(@exp, W)); % 在这里S即为相似度矩阵，也就是这不在以邻接矩阵计算，而是采用相似度矩阵%获得度矩阵DD = full(sparse(1:m, 1:m, sum(S))); %所以此处D为相似度矩阵S中一列元素加起来放到对角线上，得到度矩阵D% 获得拉普拉斯矩阵 Do laplacian, L = D^(-1/2) * S * D^(-1/2)L = eye(m)-(D^(-1/2) * S * D^(-1/2)); %拉普拉斯矩阵% 求特征向量 V%  eigs 'SM';绝对值最小特征值[V, ~] = eigs(L, num_clusters, 'SM');% 对特征向量求k-meansC=kmeans(V,num_clusters);
end

调用

clc
clf
clear
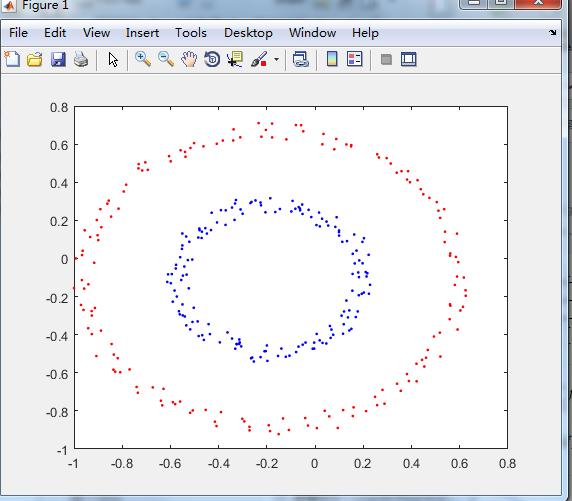
%twoCircles数据集
load('twoCircles.mat');
dataSet=twoCircles;
dataSet=dataSet/max(max(abs(dataSet)));
num_clusters=2;
sigma=0.1;
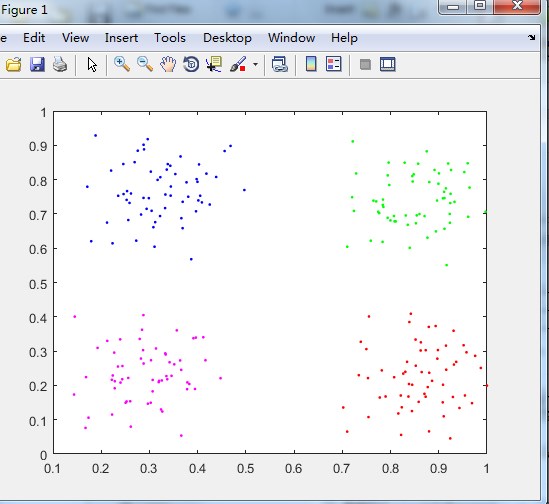
%XOR数据集
% load('XOR.mat');
% dataSet=XOR;
% dataSet=dataSet/max(max(abs(dataSet)));
% num_clusters=4;
% sigma=0.1;
Z=pdist(dataSet);
W=squareform(Z);
C = spectral(W,sigma, num_clusters);
plot(dataSet(C==1,1),dataSet(C==1,2),'r.', dataSet(C==2,1),dataSet(C==2,2),'b.', dataSet(C==3,1),dataSet(C==3,2),'g.', dataSet(C==4,1),dataSet(C==4,2),'m.');

3、结果
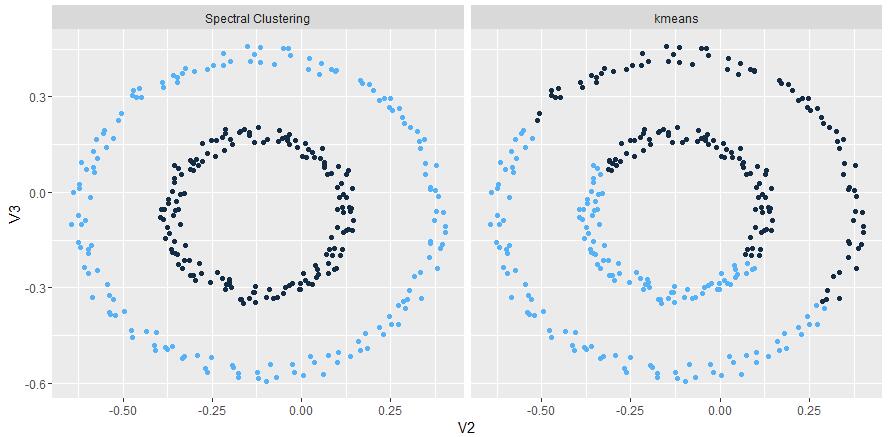
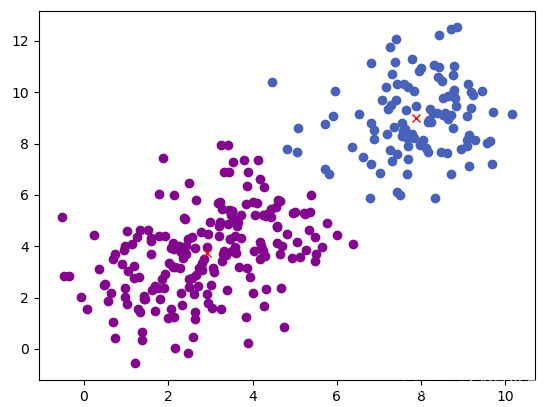
使用twoCircles数据集结果如下
这里写图片描述

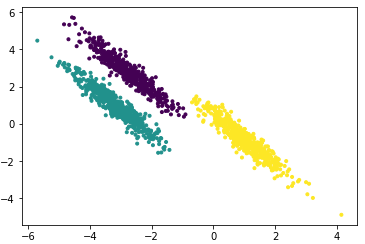
使用XOR数据集结果如下
这里写图片描述

4、数据集
twoCircles数据集
0.100267601303493 -0.0525014663431810
0.135362505728604 -0.0459654893365564
0.126933443606530 -0.0164012350510703
0.115293882173694 -0.0473205001143649
0.139683311317968 -0.0501011177695915
0.143195450367134 0.0122605442686863
0.106009774791485 -0.0168037897565408
0.118163138199935 -0.00666648250514589
0.110780653575040 0.0265235804271568
0.100737917234786 0.0156260544496707
0.126536424113384 0.0560221149798287
0.130698280785180 0.0684661165422064
0.104542664983812 0.0809424119400617
0.0726902879896738 0.0562442697844981
0.0637149247388668 0.0892398222314587
0.0853220620494712 0.0587256576192461
0.0641053278934059 0.0947081798114114
0.0540426146452954 0.106785289158448
0.0642233489137368 0.0773824972648639
0.0350076911071655 0.111209797092187
0.0575752186252200 0.139474771321149
0.0126290954650543 0.108504680216120
0.00349847022973863 0.112987536527351
0.0105711038041949 0.155177325738704
-0.0102810207109895 0.140100147985530
0.0305894017235263 0.124743038795609
0.0186284478675877 0.134335541069807
-0.0173374800758943 0.164502347969208
-0.0400122017295506 0.162977680067346
-0.0335834225808840 0.150519495750737
-0.0438278406773373 0.173784298945292
-0.0345953885966573 0.182458289569849
-0.0635677163520193 0.159022637074378
-0.0405818861039921 0.169202540121774
-0.0527891130200498 0.168094775301963
-0.0603092138248180 0.194748108368073
-0.106572021716591 0.157099440212529
-0.119891726239592 0.203801706866876
-0.0940989249650586 0.167363595210180
-0.144698032772901 0.179866876326964
-0.159434519297908 0.196417018620475
-0.146015734820454 0.189134524311375
-0.132834910083993 0.156211145302309
-0.172867395587399 0.187335748061479
-0.193854848542921 0.151202690306914
-0.211766599907447 0.197752526283055
-0.170091451059050 0.191328759522471
-0.199365119129387 0.165811645197576
-0.222213410804137 0.172067404952940
-0.214140822664785 0.185931958176438
-0.215512624668578 0.130509784136747
-0.251860997790970 0.163417827951663
-0.238942511928649 0.162858234955589
-0.276695845932721 0.154731684809285
-0.239602463560443 0.113577060960391
-0.262380455618860 0.121797461707344
-0.302793019604424 0.0905875818722080
-0.293697339739456 0.102574990330745
-0.289468524988789 0.0841848131601263
-0.278550398589779 0.0958968428628290
-0.309193942355570 0.0956952453943073
-0.309665221370501 0.101114961370419
-0.312388873911295 0.0707668589797037
-0.303505342893366 0.0692910517672390
-0.355052139807089 0.0844176064770470
-0.344861224975699 0.0741505640116930
-0.355087516529306 0.0440336650435923
-0.336475652845790 0.0563709794282264
-0.328576905148420 -0.00379063760949573
-0.356115327189969 0.0322631886597826
-0.340366743529895 -0.00564538741063073
-0.371908493540811 -0.0216241755498018
-0.360894413187727 0.00429001151502345
-0.372562268165067 -0.0339568582868362
-0.343688383714249 -0.0547917622629392
-0.358143770979545 -0.0729574893403541
-0.349822126123939 -0.0272893847258684
-0.393336391064242 -0.0537848133661400
-0.383204007322266 -0.0529678498497836
-0.353515524006840 -0.0582479249357490
-0.385827080066973 -0.0837505105693941
-0.395565518334062 -0.0794460419109608
-0.369838780380090 -0.128964105956146
-0.337849121293584 -0.101031682031104
-0.375974210376338 -0.108682708099617
-0.354766754663879 -0.155495771701691
-0.364247967067762 -0.178592840253556
-0.380703233598296 -0.146316315538511
-0.348409149249923 -0.196479292584203
-0.324568709628736 -0.166904266048153
-0.354047306608441 -0.192633432918573
-0.361878508037289 -0.189117407045915
-0.344545303997592 -0.226502649530425
-0.314056774268735 -0.213047594950611
-0.327977346511586 -0.214936421244042
-0.301897033254626 -0.259903925262516
-0.334105134733781 -0.240055452972030
-0.284924107698938 -0.222357013912615
-0.297379072167748 -0.275672884069141
-0.311400589636153 -0.262648154727971
-0.281353262796720 -0.256011103516970
-0.254789900987687 -0.283968058929749
-0.234305948705366 -0.250380189311949
-0.222139655356567 -0.271161175379960
-0.213559952965771 -0.305485551482142
-0.209975366956662 -0.289335212588093
-0.202818085453815 -0.274235106083386
-0.197541571095125 -0.297528078237609
-0.202986511362828 -0.289497670612192
-0.201700888643611 -0.284206470938609
-0.209630925383829 -0.290272082259436
-0.168298490585481 -0.335428344847537
-0.145963190943968 -0.334038327241760
-0.171474058532450 -0.337884423131229
-0.127628295490400 -0.346688626968460
-0.163836129157153 -0.348800171515015
-0.135368304936212 -0.314081776188499
-0.132007097436545 -0.313449799619478
-0.128926470738468 -0.294581296451970
-0.0902652793447816 -0.305026685606573
-0.0992012727673828 -0.329898372201677
-0.0507464573856505 -0.316762063098592
-0.0685488580119897 -0.329141751075382
-0.0444113533236343 -0.298403913030859
-0.0783191135006571 -0.332725423603294
-0.0332333013765817 -0.291940950102696
-0.0255661481044777 -0.284709797688673
-0.00245296851181924 -0.284803597794617
-0.00249863019152190 -0.305142315144786
0.0198228715332239 -0.285804165103858
0.0300100433770582 -0.287865952823912
-0.00646122214190621 -0.305561033396500
0.00428173125450494 -0.255530516108207
0.0482792519180897 -0.258225143471595
0.0123155252390966 -0.277151618583252
0.0396615132170281 -0.228522339341406
0.0416024960684403 -0.268866466045177
0.0747102721122029 -0.254810237522588
0.0436779492222656 -0.240772920306928
0.0914459988808117 -0.243627308241155
0.0970110968333145 -0.238233512837646
0.0878270794000305 -0.199494381203487
0.0765908466258044 -0.222637671377960
0.0708152910911313 -0.193570495703914
0.108928079105592 -0.198380235456279
0.0773284701063797 -0.179437889536288
0.0836765261597315 -0.142573610997107
0.0914692129480362 -0.175860041459249
0.114093997612083 -0.179336608807588
0.130382722297946 -0.115457499962721
0.144010623150724 -0.119396339545842
0.124763921481018 -0.119550424368215
0.0996057698713907 -0.109291370936644
0.116935511527647 -0.124543384023350
0.137633394319036 -0.0609595214130716
0.146950113500472 -0.0892548421397118
0.117347761318916 -0.0632817695214719
0.379647097515717 -0.0614002586252345
0.397881577085257 -0.0645688296012094
0.382685746530102 -0.0123937535394865
0.376571015503113 0.00526568870359465
0.360854505995832 0.00923618270753422
0.361534611077772 0.0167124782472926
0.379525822624179 0.0838695030300762
0.346759278173418 0.0554243132780597
0.347442760581728 0.0904281335775545
0.334523949996636 0.137099373387937
0.345257112013698 0.166779404797340
0.329850886009906 0.161630987533876
0.325478864590708 0.190771254398351
0.305729085928220 0.205005461086872
0.289377833644790 0.217239719283975
0.282662806695955 0.234449280180130
0.245906090317521 0.266819781549496
0.253842647226271 0.258021761453835
0.273989951944179 0.264725787116273
0.248765919679540 0.295404095896161
0.231178953356613 0.295397753861568
0.218352310580521 0.290136905199436
0.202267722976175 0.321104094721482
0.191437763754652 0.339566316931083
0.170554341287904 0.341721171850985
0.166129078208872 0.352545814265809
0.0967436810674985 0.383681171204894
0.0960953748434208 0.379190363603298
0.0837673594924505 0.385807952149335
0.0513156132273566 0.369505219697132
0.0193368368407719 0.386295498951418
0.0566033158446816 0.404403969159148
0.0225105750076566 0.421370129571270
-0.0316187666303336 0.430428396403566
-0.0512198377212044 0.451407595962523
-0.0375447511302303 0.450983972374145
-0.0768275219623830 0.402995944672121
-0.115035872740353 0.456288634618542
-0.114952165516496 0.409659621623729
-0.151021813205498 0.458135112803455
-0.131649339625237 0.434944387104889
-0.143705628511081 0.411955302052513
-0.219094098803580 0.399381111766744
-0.200120592939383 0.409995446343507
-0.218014262677533 0.436848150425081
-0.262938083606404 0.387899788368698
-0.246788821726377 0.399054144152815
-0.298730596387592 0.379430618109544
-0.333478792626487 0.373970635322010
-0.347918173555825 0.360435503767655
-0.323744109495305 0.390313479309319
-0.346679114506107 0.344170933324307
-0.359721999121444 0.366066149191139
-0.386243474098894 0.328875690392725
-0.390668503973189 0.346254510097211
-0.454142427723858 0.325161895529989
-0.447475711019174 0.299748117578652
-0.471869692480270 0.319336223353854
-0.472502727888249 0.304838269344423
-0.462450815819334 0.297691775190530
-0.511820295556556 0.226539941566540
-0.505467277760517 0.249540131137678
-0.551970521879217 0.195656800623545
-0.555714847641494 0.185227125097265
-0.525810838500301 0.168429835638935
-0.574289349890964 0.166809846044552
-0.545635651284044 0.141529296950356
-0.583865841637917 0.129927382439677
-0.571884196344373 0.105807686150180
-0.616270722993104 0.0954205924778298
-0.581864710787012 0.0785497954177747
-0.601703525051394 0.0725376628135345
-0.580053039284052 0.0620171518880286
-0.623464756517173 0.0114109890977535
-0.621672284794125 0.0261452976867265
-0.640064677610222 0.000108697156637055
-0.590828127767378 -0.0146681274947393
-0.623799802780419 -0.0732747659392776
-0.644908537176083 -0.100277452718236
-0.606413711833031 -0.0875732059574307
-0.617640064830947 -0.102052945534801
-0.626198284694807 -0.157330319367997
-0.597715034374953 -0.178056796073903
-0.589020489814766 -0.167580959497453
-0.619429629614866 -0.174196295521016
-0.597283540414415 -0.193338165826052
-0.597168701903739 -0.255901732252636
-0.606988796774917 -0.236188327416440
-0.572848380762827 -0.244342689069538
-0.544322309131500 -0.289631534143429
-0.585075126906007 -0.330368760062847
-0.527806671611551 -0.337602584622756
-0.538351777507918 -0.325233350555587
-0.534638277460504 -0.383351162431622
-0.539380470574240 -0.376487510734235
-0.521276649672564 -0.385241118629563
-0.496275646942683 -0.375611322249414
-0.477542224199524 -0.434961142088870
-0.474046480222339 -0.454614136269792
-0.434202530151097 -0.436340960041392
-0.412423548399363 -0.481529498157065
-0.405509437595275 -0.441323575634914
-0.408920353040217 -0.497091528299050
-0.380353653282453 -0.486610507329795
-0.361009657383465 -0.484313117375382
-0.374300424468568 -0.493141352891889
-0.334278320943441 -0.522523400728082
-0.327180651476797 -0.514420331510727
-0.292540064690979 -0.512619812658298
-0.251800146578828 -0.520182110976352
-0.263709023622946 -0.567341993513358
-0.268023520168569 -0.552560001970452
-0.194739028009272 -0.542712013354447
-0.175339173096868 -0.581755463596484
-0.189543416715458 -0.551446557340132
-0.175548554711783 -0.569770480214661
-0.123976564892378 -0.564555345969930
-0.120499554453321 -0.584365688282749
-0.0974472943526174 -0.594557046909839
-0.0701458099188990 -0.580606917064844
-0.0857861704911607 -0.541518134770355
-0.0191656181726216 -0.565571445395348
0.00473997594657107 -0.574101145702962
-0.0265136243266595 -0.540173306084224
0.0377824100859994 -0.534526125402419
0.0607127170553193 -0.573714123533801
0.0256991639305313 -0.515568692662187
0.0750293804771959 -0.513104127725868
0.100909125259251 -0.533433406421375
0.102938144215622 -0.503905120993026
0.136360882424846 -0.516724237714893
0.160351512887989 -0.468463720117496
0.165875735585508 -0.496423463021149
0.185553922917037 -0.491627279645423
0.180159052973811 -0.444826340073898
0.229183556823824 -0.448061358573410
0.219204028289945 -0.424033207830737
0.245742156083010 -0.391214678624873
0.271531239374451 -0.415838279344467
0.250818397502540 -0.414908934695387
0.271124073472142 -0.356374642544174
0.292164827520917 -0.365814651340193
0.296720828006570 -0.336049546556310
0.286019255902477 -0.343139336378628
0.335077527086029 -0.332101862006207
0.301485445863558 -0.309695995639731
0.333707792193999 -0.251151746792849
0.317821117540833 -0.264234266154152
0.381050549849280 -0.240494338034531
0.360004479542351 -0.205456598355826
0.388637523745346 -0.176202259871168
0.361675847978310 -0.159811109806494
0.395587569270693 -0.163709904402880
0.360873026344104 -0.155004205758110
0.402373685593358 -0.107735146318242
0.402966624140516 -0.126363800088237
0.373867567207756 -0.0896191882457839

XOR数据集
11.7019498550828 11.9864146917909
11.2854197541034 9.61106025805058
12.9293997424851 7.77139077294215
11.0678743631211 10.4674361646635
10.2184969161492 10.0020184568202
13.0269044940811 9.51316600308935
11.8515238069851 8.48249559804150
13.1609598294686 10.3732294253150
10.9263007068675 9.96449067911523
12.9089787789130 10.9301847688819
12.9750456160589 11.9504775516646
10.9553894933476 9.91018786085430
12.1339163659016 9.87242404255941
11.2520226218202 11.0674309284256
13.5473713727711 11.9613951483563
11.9684417926901 11.5074099651376
12.6895038389352 11.1186184934507
10.2832003244487 11.5415772866841
12.4229965264968 11.1877890494122
10.1643053902437 10.5663656603295
11.2048464152179 9.71682231158900
11.0806034399502 10.1652955523462
12.2846926890514 9.78779540958933
10.1824985132917 12.8606632258936
12.0979543910706 11.9424610915524
12.7060709470499 11.5447724445084
12.0561173728298 9.81784926866268
14.0689074539149 9.96319738455191
12.6497443989402 10.4276846525517
12.0319954734513 9.49339677197864
13.4474308028544 11.5983168358328
11.0632839042566 10.2491041959578
11.2335208151750 11.9891784117950
13.0220342253125 9.87449708893778
11.9246891549662 11.4344269572793
11.7350618936693 9.81397193906283
12.3694859565937 8.90011903885874
12.8668333962113 9.26621804504976
12.3472189846887 12.4519494691887
13.0461983679146 10.7051037792115
13.5613776434838 9.75964665916580
11.3885956114862 9.79139688756874
12.8567032866785 10.7863262984152
13.0367032355283 10.3257802151620
11.4431349243099 9.57049805828306
10.7881498467560 10.4238566446530
11.7937409546202 9.42825780195812
10.8695035815800 10.3935413749975
11.2069340930752 11.4638602435525
10.7110735083414 8.77581178255715
12.8663476177943 10.5273375271888
12.8217630762208 10.5196712293077
11.9372510678886 11.2111052801608
11.4063244993183 9.57256514219680
13.0592013597650 11.6844988802191
11.0557080731010 8.72797402070974
12.6163563860771 9.15860434653811
13.6011577253520 10.9612000658453
10.0219686555893 8.52703640672761
12.5759972338184 11.6862204932952
3.94956748525547 4.73412736306845
3.56443650819659 2.16105751188226
5.16518645299920 0.757482840173608
3.61304847623052 3.12958148239127
2.02743183857526 2.44647254909842
5.33618619679163 2.66809927032053
3.68775438397887 1.12528095586246
4.88035607726594 3.21563173831697
3.13360464755309 3.05228676423534
4.95911647587894 3.68941297928373
5.03377110970780 5.08681762596579
3.21733424525325 2.70489533613306
4.50420188070526 2.95583990952738
3.20224063526126 4.17147835875988
5.80938097113020 4.80370056173962
3.98460038265991 3.92698758869092
5.13143299162650 3.84947637366477
2.71611714352392 4.36588678351726
4.27943751872594 3.85805947284429
2.37776612705653 3.16341945842501
3.38709557974511 2.93854349655031
3.22134277707462 2.99521696172944
4.75463372140937 3.07556636384569
2.04727753976733 5.65184622135477
4.01602846655169 5.11157547894071
4.42528548810412 4.34156396152200
4.59594684317470 3.02636336455003
6.31445932888745 3.11827448355900
4.72920762388907 3.20508019738685
4.27131243449136 2.10941568794003
5.59214691338119 4.78872405379976
3.31059538454970 3.59840810780763
3.37740674917462 4.71674384587023
5.34308084589231 2.94576145938952
4.04718446074330 4.27307193986623
4.32876651779016 3.04747253465181
4.18816258899334 2.06897329128835
4.57263166946153 1.83347159054448
4.05691644921189 5.71392994789072
4.70978973888974 4.09497593284296
5.56595763934141 2.67407011567151
3.43696852355266 3.07567791069570
4.82251946351670 3.77435235372370
5.40020787637713 2.88053256381809
3.67103130392403 2.17036088114051
3.16013023231025 3.23081148179191
4.32659452489903 2.57696352017381
3.44224443558299 3.61912519078363
2.99896244250298 4.65382327349707
2.44994771117056 1.49433602795614
5.16261395487731 3.46140165455953
4.51558310299567 3.00962190807828
4.06265547174795 3.72281102435404
3.53666871771116 2.10885769113510
5.52034117115833 4.76315118501930
3.14056140665305 1.62315103979940
4.60981274729235 1.74831475255569
5.87258886502605 3.85620589083548
2.36322659904347 1.07464462870429
4.69604970120875 4.14119464020140
4.06185144741150 12.7220620980209
4.34886439894051 9.33148953493914
5.45675677090613 8.01527509074562
4.21658191498141 10.5263808010244
2.99185450579116 9.52046731867536
5.76867119076199 10.3521953372825
4.38250657859681 8.52766928855863
5.63845535255539 11.1984669397109
3.56624697370019 10.4544707494578
5.61461451568248 11.3100849264833
5.14352616043085 12.2411874314451
4.15109409363858 10.0862405405775
4.69166268712695 10.1169738813767
3.46841947416890 11.9295907900873
6.60721123134179 12.6748116836550
4.47220415809383 11.2777643335768
5.90039125568537 11.5350120824123
3.11212388874180 11.6600354172851
4.55237631284963 11.3886887767012
2.41500076112686 10.9958428447102
4.06039049385377 10.5360336884229
3.65090723632647 10.3305282924347
5.20637295631411 10.3747913871788
2.65713470905755 13.1044387629241
4.07543176340997 12.5342211321612
4.74109692644298 11.7011702794942
5.36866897403764 10.5846825644193
7.01089231789354 10.8608198492609
4.85453980499825 10.6294149810125
4.40146388488079 9.53877147651624
5.68449925210039 11.9135968125196
3.31841567811904 10.6228421238580
3.80051613433878 12.0069291110010
5.99865402083022 10.2632820422887
4.77010698543533 11.9267620738327
4.85997581137260 11.0044084587225
4.29698052726639 10.0047041640732
5.20439804299001 9.29135792439885
4.18341631454120 12.9544083447228
4.84409304320332 11.8588738771294
5.66455173205240 10.4333974988026
3.57899577198459 10.8163259756743
4.99077076200823 11.5180406952110
5.59645679863409 9.98645298055085
3.98851107907347 9.85192131161083
3.47655923145655 10.6940720603856
4.54415783432186 9.78912672542875
3.69328628159872 10.7176439284717
3.89188484778896 12.4773977474249
3.15317093572685 8.66934576533822
5.71835189759670 10.6249715643445
4.70001677075332 10.6756091244894
4.27468631428027 11.6172003997083
3.61401552582384 9.62541589948637
6.43414158193790 12.4658534919698
3.84727662434998 8.77674141641880
5.16760171404722 9.70177182244194
6.18601785496265 11.3970899720770
2.52943016194562 8.75437852691476
5.31854696048865 11.1777576582499
12.1703648499568 4.25918068096871
11.9156935980092 1.76634249140915
13.0358935269100 0.642543539262382
11.7216268152551 3.38130061163330
9.90505798227448 1.91274110674955
13.4662062554524 2.40759813336150
11.5984550563205 0.786001029812625
12.3780421908777 2.75307429834405
11.0339125426674 3.44025981373637
13.2106593276639 3.79077541277182
12.4088411893229 5.22773814000357
12.1122686730571 2.14488253438531
12.5043505310139 3.00969778829176
12.0213980690701 4.70806434172846
13.4275882046496 4.47432208674284
12.3191249275729 4.27068576380739
13.1438229453726 3.67926012471611
10.4191659275932 4.61631800150300
12.0283877080530 3.63183656076588
10.3614842954338 3.24329337255066
11.9219140465917 2.84883376285038
11.1437998741670 2.36630631875367
11.8286230610643 2.87946675115601
10.6578203885544 5.65868817981521
12.6095626497045 5.26533359557208
12.9114522235639 4.45809181302457
12.2806675275436 2.47582686999720
14.1116937595625 2.81457524522844
12.8243093305766 2.84866696078969
12.8169655828713 2.12540787718603
13.1338518477016 5.07021406788503
11.3941898892237 3.16009759933799
11.8395114291177 5.42887609283455
13.6728369339630 2.09169395351962
12.1765374909825 4.59471373669116
12.2008728392924 3.37028124200855
12.3161807588698 2.35728531555062
12.8462392101779 1.55075367097960
11.8838569369266 5.76980383297941
13.5110179090073 4.18356739321067
13.3050352786948 1.89344066723256
10.9742696810326 2.32386257172529
12.9186180175458 3.46762198079446
13.1141431772837 2.34692534478435
11.5167277073615 1.66791119261036
11.6610124480111 3.30769293319020
11.8129296060640 2.36417920344874
10.6285971666362 3.12236573026102
10.5813925840179 4.31579294391233
10.6435550321234 1.51959044206070
12.6586543018011 3.92202585689097
12.4203408497795 3.34244887851811
11.7719738365109 3.79262098178588
11.5883744422229 2.40673990807543
13.7647233821169 4.03761334193030
11.6179516027426 1.92225568194860
12.4155917435700 0.931081755088327
13.9315067764341 3.53992252705657
10.0194033879627 0.920979800389733
12.6752472116720 4.27580101528130