定义
哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树。所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。树的路径长度是从树根到每一结点的路径长度之和,记为WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln),N个权值Wi(i=1,2,...n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,...n)。可以证明哈夫曼树的WPL是最小的。
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
实例引入
现在有这样一个经典问题:果子合并。
现在得到很多果子,需要把这些果子合并成一堆。每一次合并,可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过 n−1 次合并之后,就只剩下一堆了。在合并果子时总共消耗的体力等于每次合并所耗体力之和。
假定每个果子重量都为 1,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使耗费的体力最少,并输出这个最小的体力耗费值。
例如有 3 种果子,数目依次为 1,2,9。可以先将 1、2 堆合并,新堆数目为 3,耗费体力为 3。
接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 12,耗费体力为 12。所以总共耗费体力=3+12=15。可以证明 15 为最小的体力耗费值。
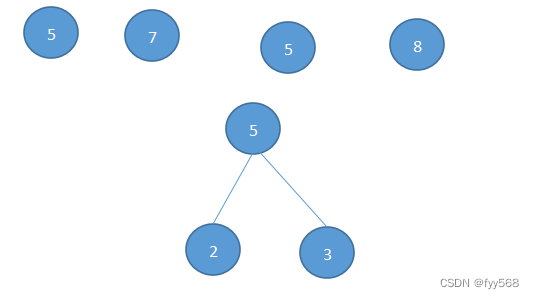
我们把这几个果子看成树的叶子

然后通过逐次合并其中两个叶子(果子),使根节点的权值最小,根据上面的分析先合并1,2得到3,之后合并3,9得到12。其中我们要计算的便是产生的新节点的权值,把这先权值相加,即是最后要求的体力值。
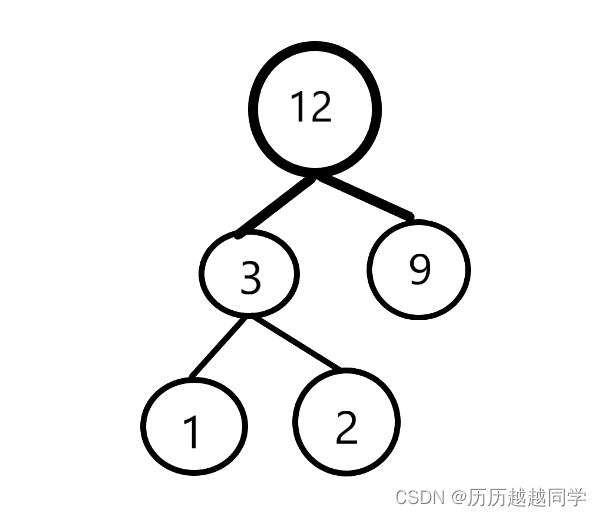
进一步分析可以发现,假设初始状态下我们有四个点,是四个点之间的最优解问题,当我们合并其中两个点之后就变成了三个点的最优解问题,以此类推;而且如果保证每次选的两个数都是最小的(最优的),那么接下来都是最优解的情况了。
由于数据输入是并不是按照从小到大排列,故可以使用小根堆来做。
代码
#include <bits/stdc++.h>
using namespace std;
int main()
{int n;scanf("%d", &n);priority_queue<int, vector<int>, greater<int>> heap;while (n--){int x;scanf("%d", &x);heap.push(x);}int res = 0;while (heap.size() > 1){int a = heap.top();heap.pop();int b = heap.top();heap.pop();res += a + b;heap.push(a + b);}printf("%d\n", res);return 0;
}