学习笔记，仅供参考，有错必纠

---

---

时间序列

ADF检验

如果被检验的真实过程是一个AR§ 过程，而检验式是AR(1)形式，那么由于对$y_t$形式的设定错误，检验式对应的误差项必然表现为自相关。因为假定检验式误差项是非自相关的，所以当误差项具有相关性时，回归参数的检验统计量不再服从DF分布.

如果$\rho =0$成立，则$y_t$含有单位根。称此检验为ADF（增项或扩展的DF）检验。称此统计量为ADF统计量。

注意，只有在样本容量充分大的前提下，才可以用表1的第1部分中的临界值。因为在小样本条件下ADF分布与DF分布不一样。

与上面的讨论相仿，在ADF检验式中也可以加入漂移项$\mu$和时间趋势项t。同理这些临界值也是在样本容量充分大的前提下才可用。对于下式：
$$\Delta y_t=\rho y_{t-1}+\sum {\varphi }_j^{\ast }\Delta y_{t-j}+\mu +u_t$$
原假设认为$y_t$是一个非平稳过程，备择假设认为$y_t$是一个均值非零的平稳过程。

对于下式：
$$\Delta y_t=\rho y_{t-1}+\sum {\varphi }_j^{\ast }\Delta y_{t-j}+\mu +\alpha t+u_t$$
原假设认为$y_t$是一个非平稳过程，备择假设认为$y_t$是一个确定性趋势平稳过程。

ADF检验式也可以扩展到d.g.p.带有移动平均成分的情形。只要检验式中的附加项$\Delta y_{t-j}$充分多，就能够对ARMA(p,q)形式的$y_t$做很好的近似，从而保证*$u_t$*为白噪声。因为实际中$y_t$的具体形式未知，所以差分滞后项个$\Delta y_{t-j}$数的选择非常重要。滞后项个数太少，会导致当原假设为真时，拒绝原假设的概率变大。当滞后项个数太多时，又会导致检验功效降低（当备择假设为真时，检出的概率变低）

有人主张通过附加项是否具有显著性以及调整的可决系数确定ADF检验式中差分滞后项的个数。如果是线性检验式，这种判别方法与赤池准则是等价的。也有人认为用调整的可决系数判别滞后项数不尽如人意。各种形式（ARMA、AR、MA）的$y_t$的蒙特卡罗试验结果显示这种判别方法存在一些问题。所以Schwert建议用下式确定最佳滞后期数k：
k = i n t { 12 ∗ ( T / 100 ) 1 / 4 } k = int \{ 12*(T/100)^{1/4} \} k=int{12∗(T/100)1/4}

• 例子

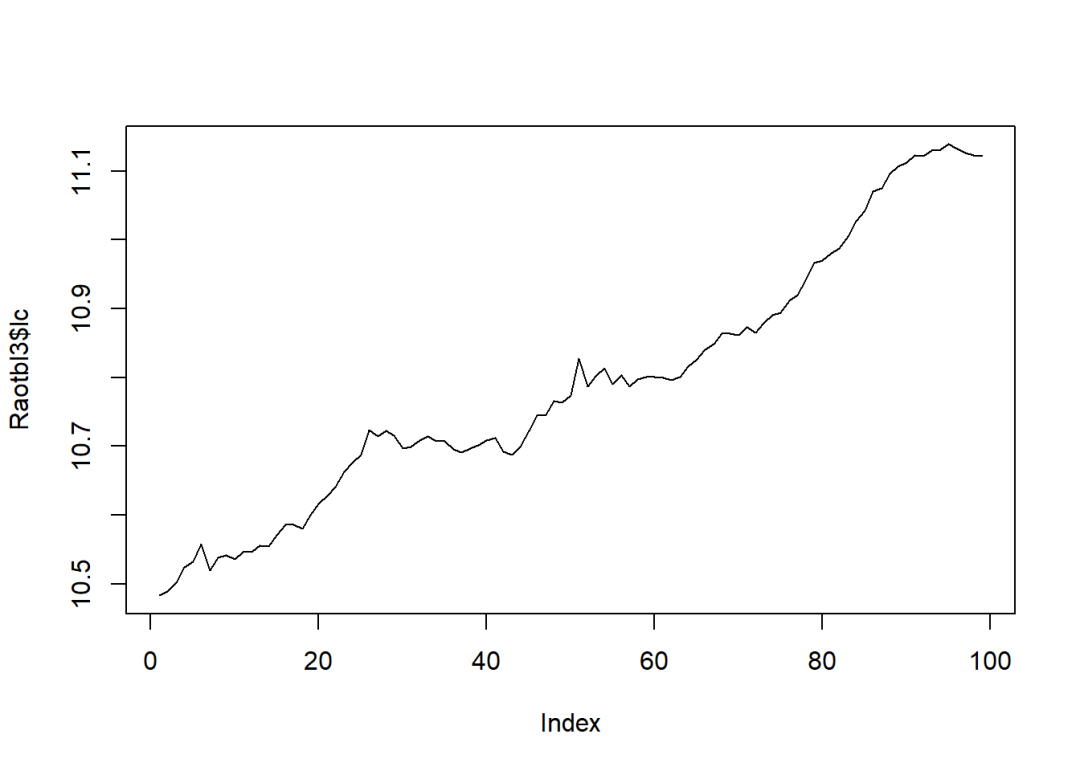
深圳综合成指收盘价序列如下图，检验是何种过程.

多重单位根的检验方法

Dickey and Pantula（1987）对此提出异议。他们认为当$y_t\sim I(2)$时，备择选择是，$y_t\sim I(1)$而单位根检验的备择假设是$y_t\sim I(0)$。出现了不一致。这时需要检验的是$\Delta y_t$是否为平稳序列。所以正确的检验程序应该是首先对$y_t$取足够次数的差分，从而保证被检验序列为平稳序列。然后每次用减少一次差分次数的序列依次进行单位根检验。直至接受原假设为止。从而判断出$y_t$的单整阶数

当$y_t\sim I(2)$时，${\Delta }^2{y}_t\sim I(0)$，首先应该做如下检验：
$${\Delta }^2{y}_t=\rho y_{t-1}\sum _{j=1}^k{\varphi }_j^{\ast }{\Delta }^2{y}_{t-j}+u_t$$
如果结论是接受原假设，则$y_t\sim I(2)$有两个单位根。

如果结论是拒绝原假设，则再次检验$\Delta y_t\sim I(0),y_t\sim I(1)$. 这种检验顺序才合理.

实际中，经济时间序列的单整阶数不会超过2。所以对序列进行单位根检验的顺序应该是${\Delta }^2{y}_t,\Delta y_t,y_t$ .

Dickey and Pantula基于蒙特卡罗模拟的结论显示，当序列$y_t$含有多重单位根时，从$y_t$开始检验单位根，则拒绝原假设的能力有所下降。

结构突变与单位根检验

Perron指出，如果被检验过程是一个退势平稳过程，并且在考虑的期间内存在趋势结构突变。如果不考虑这种趋势突变，当用ADF统计量检验单位根时，将会把一个带趋势突变的退势平稳过程误判为随机趋势非平稳过程。即进行单位根检验时不考虑结构突变，会导致检验功效降低（实为退势平稳过程，检验结果却认为是单位根过程）。同样，当进行单位根检验时，不考虑漂移项存在突变，或不考虑趋势项、漂移项同时存在突变，也会导致单位根检验功效降低。

• 例子

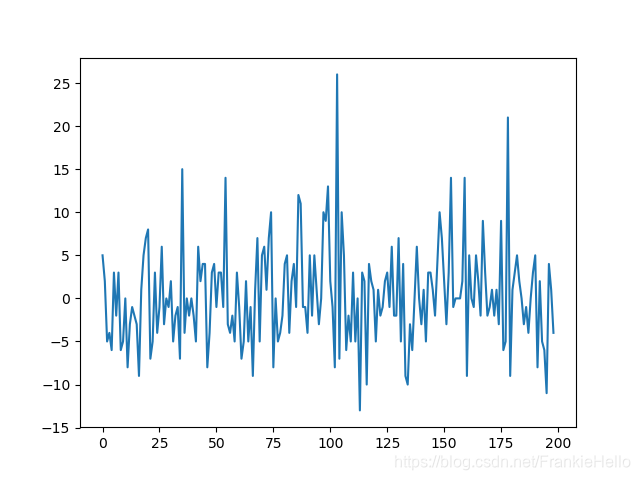
如下图，有T=100的均值突变平稳过程$y_t$：

用虚拟变量（D=0，（1-50）； D=1，（51-100））区别突变前后两个时期，得ADF检验式如下：

外生性结构突变点的检验方法

结构突变点已知时，称其为外生性结构突变点。假定发生结构突变的时点已知为$t_B$，则发生在截距的突变为${\mu }_0+{\mu }_1{D}_t$，其中:
$$D_t=\{\begin{array}{ll}1,& t>t_B\\ 0,& t<t_B\end{array}$$

当突变发生在斜率而截距不变时，对应的模型为:

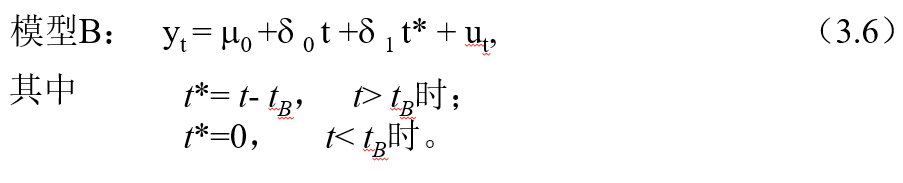
由于斜率反映增长率，因此也称模型B为变化的增长率模型.

当截距和斜率同时具有结构突变时，对应的模型C为：
$$y_t={\mu }_0+{\mu }_1{D}_t+{\delta }_{0}t+{\delta }_1{t}^{\ast }+u_t$$
对于模型A，B，C，原假设和备择假设为：
$$\begin{gathered} H_0:u_t\sim I(1) \\ {H}_1:u_t\sim I(0) \end{gathered}$$
当$u_t\sim I(1)$时，$y_t$为结构突变的单位根过程，而$u_t\sim I(0)$时，$y_t$为结构突变的趋势平稳过程。

基于上述分析结构突变的单位根检验就转化为对退化趋势之后的残差的单位根检验，其具体的检验步骤和方法如下：

结构突变的单位根检验的渐近临界值:

• 例子

中国某指标的时序图如下：

ADF检验式是：

若以1978年为结构突变年，令D=0, (1953-1977)；D=1, (1978-1997)；1952年，t =1。得带有趋势突变点的ADF检验式如下：

内生性结构突变点的检验方法

在不知道突变点位置的情形下，Banerjee, Lumsdaine and Stock（1992）应该用通常的ADF统计量或用递归法、滚动回归法和序贯回归法所有子样本计算的ADF统计量中的最小的一个用来做上述3种检验检出突变点。

• 递归法

以原样本的第一个观测值开始用k0个观测值构成第一个子样本。然后在第一个子样本基础上按顺序每次增加一个观测值构成一系列子样本，一直到还原整个样本范围。子样本容量用数学符号表示为：

• 滚动回归法

滚动回归法与递归回归法有些类似。也是通过子样本计算统计量的值，只不过子样本的容量不是逐步扩大，而是保持一个定值，从{1, 2, …, k}, {2, 3, …, k+1}, …, 一直到子样本{ T- k+1, T- k +2, …, T}。建议k =0.3 T。用每个子样本按（8）式做单位根检验。用其中最小的ADF(k/T)值与表6中的滚动回归法临界值做比较检验单位根。H0：r = 0，存在单位根。

• 循序回归法

设突变点发生在k期，循序回归法是用整个样本按下式回归，并求ADF值：

在不知k期的具体位置时，可以令k逐期增加。每次都计算ADF(k/T)值，然后用最小的ADF(k/T)值与表7中的临界值比较。另一个功效比较好的检验统计量是F统计量。对于趋势突变和均值突变两种情形，原假设都是${\alpha }_2=\rho =0$。从循序的F值中选最大的一个与表7中的临界值比较，看能否推翻原假设。