概念

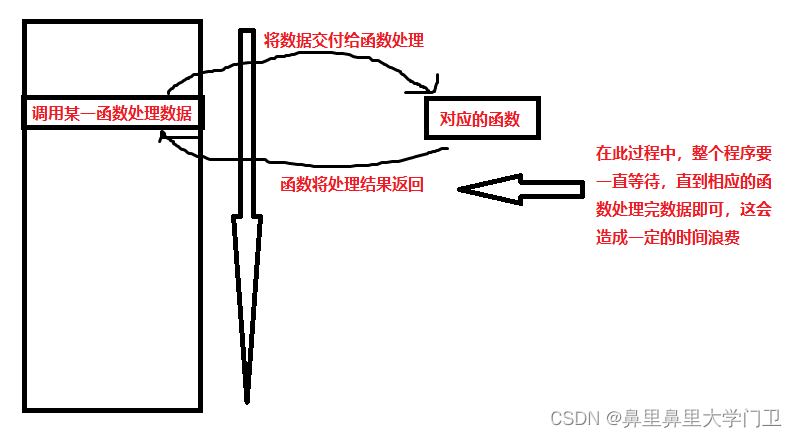
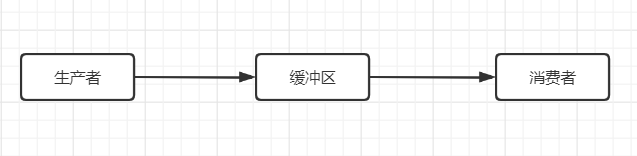
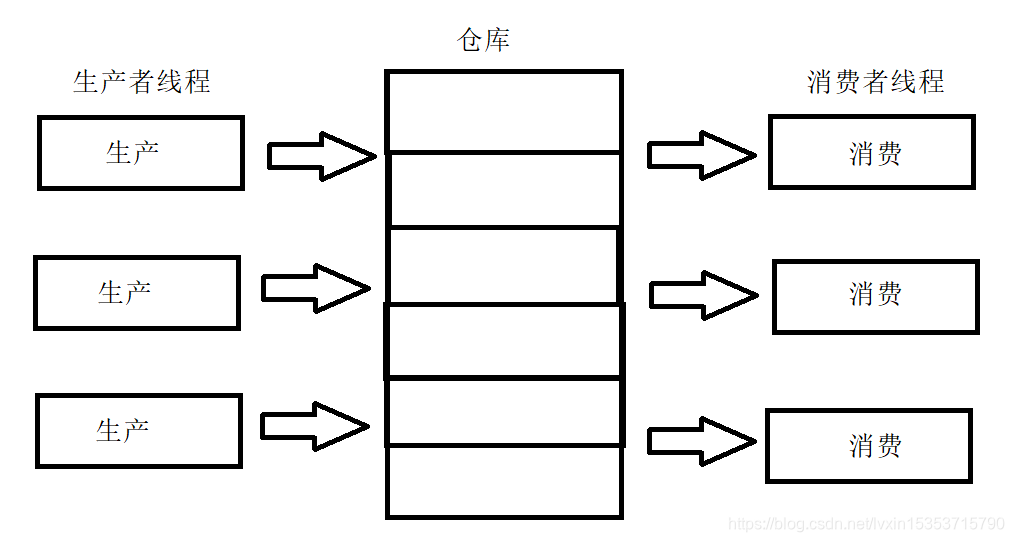
生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题。生产者和消费者彼此之间不直接通讯，而通过阻塞队列来进行通讯，所以生产者生产完数据之后不用等待消费者处理，直接扔给阻塞队列，消费者不找生产者要数据，而是直接从阻塞队列里取，阻塞队列就相当于一个缓冲区，平衡了生产者和消费者的处理能力。这个阻塞队列就是用来给生产者和消费者解耦的。

321原则

• 三种角色：生产者、消费者、仓库
• 两种关系：生产者与生产者之间是互斥关系，消费者与消费者之间是互斥关系，生产者与消费者之间是同步与互斥关系。
• 一个交易场所：仓库（这里我们用阻塞队列来表示）

优点

• 解耦–生产者。消费者之间不直接通信，降低了耦合度。
• 支持并发
• 支持忙闲不均
  

代码实现

基于BlockingQueue的生产者消费者模型
BlockingQueue 在多线程编程中阻塞队列(Blocking Queue)是一种常用于实现生产者和消费者模型的数据结构。其与普通的队列区别在于，当队列为空时，从队列获取元素的操作将会被阻塞，直到队列中被放入了元素；当队列满时，往队列里存放元素的操作也会被阻塞，直到有元素被从队列中取出(以上的操作都是基于不同的线程来说的，线程在对阻塞队列进程操作时会被阻塞)

  //这是生产者消费者模型的代码                                                                                                                   #include<iostream>#include<queue>#include<stdlib.h>#include<pthread.h>#include<unistd.h>#define NUM 8  class BlockQueue{private:std::queue<int> q;int cap;pthread_mutex_t mutex;pthread_cond_t full;pthread_cond_t empty;private:void LockQueue()  //队列加锁{pthread_mutex_lock(&mutex);}void UnlockQueue()  //队列解锁{pthread_mutex_unlock(&mutex);}void ProductWait()  //队列满，生产者等待{pthread_cond_wait(&full,&mutex);}void ConsumeWait()  //队列空，消费者等待{pthread_cond_wait(&empty,&mutex);}void NotifyProduct()  //队列不为满时，通知生产者{pthread_cond_signal(&full);}void NotifyConsume()  //队列不为空时，通知消费者{pthread_cond_signal(&empty);}bool IsEmpty(){return (q.size() == 0 ? true : false);}bool IsFull(){                                                                                                                                          return (q.size() == cap ? true : false);}public:BlockQueue(int _cap = NUM):cap(_cap) //构造函数{pthread_mutex_init(&mutex,NULL);pthread_cond_init(&full,NULL);pthread_cond_init(&empty,NULL);} void PushData(const int &data){LockQueue();while(IsFull()) //队列满{NotifyConsume();std::cout<<"queue full,notify consume data,product stop!!"<<std::endl;ProductWait();}//队列不满,生产者插入数据，通知消费者队列中已经有数据了q.push(data);NotifyConsume();UnlockQueue();}void PopData(int &data){                                                                                                                                          LockQueue();while(IsEmpty())  //队列为空{ NotifyProduct();std::cout<<"queue empty,notify product data,consume stop!!"<<std::endl;ConsumeWait();}//队列不为空data = q.front();q.pop();NotifyProduct();UnlockQueue();}~BlockQueue(){pthread_mutex_destroy(&mutex);pthread_cond_destroy(&full);pthread_cond_destroy(&empty);}};//消费者void* consumer(void* arg){BlockQueue *bqp = (BlockQueue*)arg;int data;for(;;)                                                                                                                                      {bqp->PopData(data);std::cout<<"Consume data done: "<<data<<std::endl;}}//生产者void* producter(void* arg){BlockQueue *bqp = (BlockQueue*)arg;srand((unsigned long)time(NULL));for(;;){int data = rand()%1024;bqp->PushData(data);std::cout<<"Product data done: "<<data<<std::endl;// sleep(1);}}int main(){BlockQueue bq;pthread_t c,p;pthread_create(&c,NULL,consumer,(void*)&bq);pthread_create(&p,NULL,producter,(void*)&bq);pthread_join(c,NULL);pthread_join(p,NULL);return 0;}

运行结果：