D - 最长公共子序列问题
Description
给定两个序列 X={x1,x2,…,xm} 和 Y={y1,y2,…,yn},找出X和Y的最长公共子序列。
Input
输入数据有多组,每组有两行 ,每行为一个长度不超过500的字符串(输入全是大写英文字母(A,Z)),表示序列X和Y。
Output
每组输出一行,表示所求得的最长公共子序列的长度,若不存在公共子序列,则输出0。
Sample
Input
ABCBDAB BDCABA
Output
4
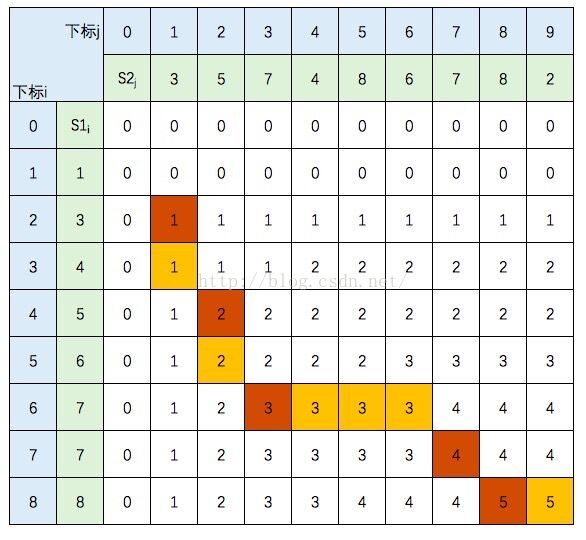
本题建表填表来解决
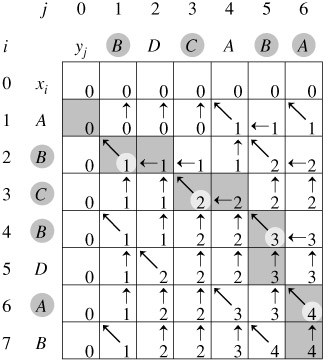
先写出状态转移方程
if (a[i-1]==b[j-1])//如果两字符相同
dp[i][j] = dp[i - 1][j - 1] + 1;//该位置赋值为左上角数加1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);//该位置赋值为上个位置和左边位置中较大的一个以下是ac代码
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int dp[501][501] = { 0 };//初始化表格
int main()
{string a, b;int i, j;cin >> a;cin >> b;int n = a.length(), m = b.length();for (i = 1; i <= n; i++).//此处比较抽象,是a,b这两个字符串列成表格形式{for (j = 1; j <= m; j++){if (a[i - 1] == b[j - 1])//填表{dp[i][j] = dp[i - 1][j - 1] + 1;}else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}cout << dp[n][m] << endl;return 0;
}本题至此便结束了,但笔者想到如果想输出这个lcs应该怎么写呢,翻阅了一些大佬的博客,发现这个问题是最长公共子序列的回溯问题。
思路是建表的同时记录该位置的数据来源(来自左上角,左边,右边这三种情况),然后通过记录下来的方向进行回溯,用递归实现这个过程。
#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int dp[501][501] = { 0 };
int memory[501][501];//记忆表
string a, b;
void lcs(int n, int m)//找到lcs并且填dp表和记忆表
{int i, j;for (i = 1; i <= n; i++)//对记忆表的初始化最左一行赋1,最上一列赋-1memory[i][0] = 1;for (i = 1; i <= m; i++)//这两个赋值是为给递归输出函数一个边界memory[0][i] = -1;for (i = 1; i <= n; i++){for (j = 1; j <= m; j++){if (a[i - 1] == b[j - 1]){dp[i][j] = dp[i - 1][j - 1] + 1;memory[i][j] = 0;//标记值来自左上角的位置为0}else if (dp[i - 1][j] >= dp[i][j - 1]){dp[i][j] = dp[i - 1][j];memory[i][j] = -1;//标记值来自上边的位置为-1}else if (dp[i - 1][j] < dp[i][j - 1]){dp[i][j] = dp[i][j - 1];memory[i][j] = 1;//标记值来自左边的位置为1}}}
}
void output(int n, int m)//根据记忆表的标记,按方向回溯输出lcs
{if (n == 0 || m == 0)return;else if (memory[n][m] == 0){output(n - 1, m - 1);cout << a[n - 1];//该行会进入栈区,因为先进后出的原则,会从前往后按输入顺序次打印lcs}else if (memory[n][m] == -1){output(n - 1, m);}else if (memory[n][m] == 1){output(n, m - 1);}
}
int main()
{int i, j;cin >> a;cin >> b;int n = a.length(), m = b.length();lcs(n, m);output(n, m);return 0;
}