算法14-求最长子序列

article/2025/9/28 9:58:32

题目：
给定数组arr。求最长的有序子序列的长度，返回长度int

分析：
1 要求的子串是有序的，就要比大小
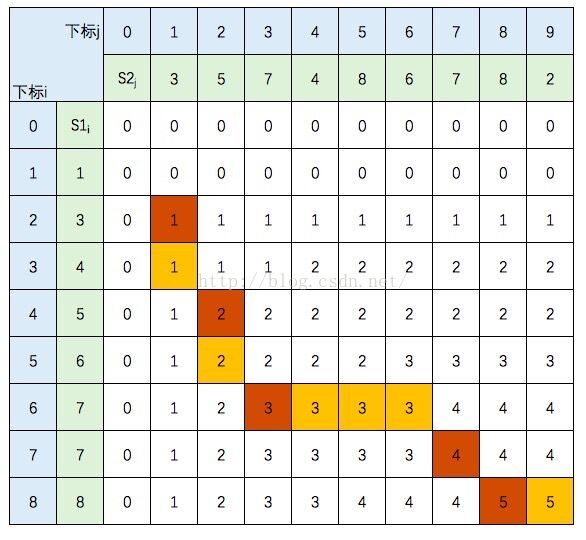
2 用最暴力大方法，看成窗口问题，每一个元素求出它左边的最长序列子串，写入一个数组dp，dp中的最大值就是要求的结果，这样的方法时间复杂度为O(N^2)
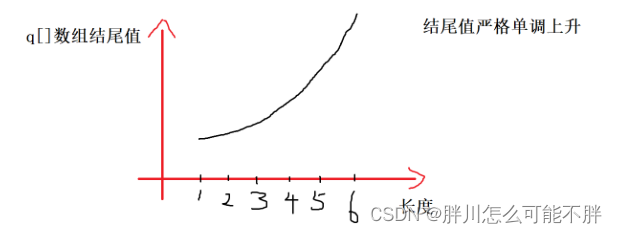
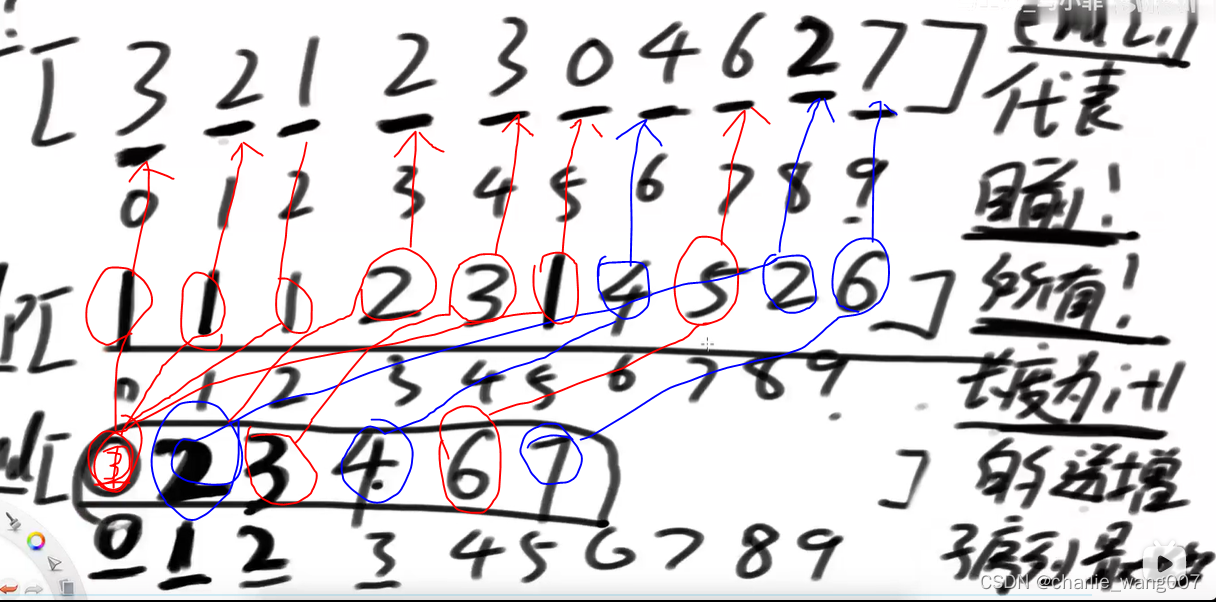
3 进阶算法：除了记录每个元素与左边的最大序列子串的数组dp外。再建一个数组end，其实在使用上相当于一个有序链表，每一个元素插入的位置是固定的，就是它要替换第一个大于它的值，若end中最后一个元素比要插入的元素还小，就append到end末尾，这样end中从0开始到插入的元素的长度，就是插入元素的最大有序子序列长度

//利用两个数组，遍历list，步骤：

//1 先将第i个元素放入end：

当i的值小于当前end的最后一个元素，则插入end中第一个大于i的值；
否则就append到end的最后

//2 将插入end的位置+1记入dp表，返回dp中最大值

在这里插入图片描述

代码：
两种时间复杂度的解法

package main
import("fmt"
)
// list:=[]int{4,1,3,2,3,9,5,6,9}
//窗口   O(n^2)
func process(list []int){dp:=[]int{1}for i :=1;i<len(list);i++{max:=0fmt.Println(list[i])fmt.Println(dp)cours:=ifor cours>=1{if list[cours-1]<list[cours]{if dp[cours-1]>max{max=dp[cours-1]}}cours--fmt.Println(cours)}dp=append(dp,max+1)}fmt.Println(dp)
}
//O(N*LOGN)
//利用两个数组，遍历list，
//1 先将第i个元素放入end：当i的值小于当前end的最后一个元素，则插入end中第一个大于i的值，否则就append到end的最后
//2 将插入end的位置+1记入dp表，返回dp中最大值
func process1(list []int){end:=[]int{list[0]}//第i个元素，替换end中大于它的第一个数，插入的位置+1就是它的最长子序列，并更新到dp对应的位置dp:=[]int{1}//用来记录第i个元素的最长子序列，值来自于将数据插入end后end的长度（长度是从1开始，即个数）fmt.Println(dp)fmt.Println(end)for i :=1;i<len(list);i++{fmt.Println(list[i])//如果i的值小于end中最后一个的值，找到第一个大于i的值，替换它if end[len(end)-1]>=list[i]{fmt.Println(end[len(end)-1],list[i])idx,j:=-1,1for {//目标值每次加1，从数组中找到它后退出，否则返回-1fmt.Println(end,list[i]+j)idx,_=binsearch(end,list[i]+j)fmt.Println(idx)j+=1if idx!=-1{//不等-1表示找到了，退出break}}end[idx]=list[i]fmt.Println(end)//把插入end的位置+1记录到dp中，这个值就是i的最长子序列dp=append(dp,len(end[0:idx+1]))}else{如果end的最后一个元素小于i的值，就直接append到end，将end的长度+1记录到dpend=append(end,list[i])dp=append(dp,len(end))}}fmt.Println(end)fmt.Println(dp)}
func binsearch(list []int,tar int) (int,int){left:=0right:=(len(list)-1)for left<=right{mid:=(left+right)/2idx:=mid// fmt.Println(mid)if list[mid]==tar{return idx,list[idx]}if list[mid]>tar{right=mid-1idx=right}else{left=mid+1idx=left}}return -1,-1}
func main(){list:=[]int{1,3,5,6,7,47,18,22,35,25,40,42,9}// list:=[]int{3,2,1,2,3,0,4,6,2,7}process1(list)// fmt.Println()// list:=[]int{1,3,5,6,7,9,18,22,35,36,40,42,47}// fmt.Println(binsearch(list,3))}