(在研读大佬写的博客后,打算记录下自己学习过程)
通过最长上升子序列的拓展了解到,其实这是一个系列的问题主要代表有:
1 最长上升子序列
2 最长不上升子序列
3 最长下降子序列
4 最长不下降子序列
就以最长上升子序列为例。(注意:这里面说的子序列不连续的)
得到一个数组,求这个数组的最长上升子序列长度
3 1 2 1 8 5 6可以直接看出来这个数组的最长上升子序列是1 2 5 6,其长度也就是4.一眼就能看出来,但是用代码该怎么实现呢?
介绍俩种方法:
dp思想
只能用于数据小的情况,要不然会TLE
目前为止所接触的dp思想核心就在状态转移方程上。同时也用到了贪心的思想。在所有的上升序列中最开始的长度都是1(算上它自身)。那么这个时候就只要考虑以arr[i]结尾的子序列中使其最长即可。找到arr[i]然后在从头开始枚举,只要满足arr[j]<arr[i]都给他塞进去从而去取max值
brr[1]=1 (本身长度为1)
brr[2]=1;
brr[3]=2;
brr[4]=1;
brr[5]=3;
.......以此类推
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
//#include<unordered_map>
#include<map>
#include<cstring>
//#include <unordered_set>
#include<queue>
#include<set>
#include<stdlib.h>
#define dbug cout<<"hear!"<<endl;
#define rep(a,b,c) for(ll a=b;a<=c;a++)
#define per(a,b,c) for(ll a=b;a>=c;a--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
#define endl "\n"
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
typedef pair<long double,long double> PDD;
const int N = 4e5 + 5;
const int INF = 0x3f3f3f3f;
//const ll LINF=LLONG_MAX;
// ll gcdd(ll a, ll b)
// {
// while(b^=a^=b^=a%=b);
// return a;
// }
// void add(ll a,ll w)
// {
// noda[++idx].b=w;
// noda[idx].ne=h[a];
// h[a]=idx;
// }ll h[N],idx;
const ll mod =1000000007;
ll t, n,a,b,c,d, m, x,y, k, cnt, ans, ant, sum,q,p,num;
ll arr[N],brr[N], crr[N];
bool book[N];int main()
{IOS;cin>>n;for(ll i=1;i<=n;i++){cin>>arr[i];}for(ll i=1;i<=n;i++)//最长上升子序列{brr[i]=1;for(ll j=1;j<i;j++){if(arr[i]>arr[j]){brr[i]=max(brr[i],brr[j]+1);}}}for(ll i=1;i<=n;i++)//最长下降子序列{brr[i]=1;for(ll j=1;j<i;j++){if(arr[i]<arr[j]){brr[i]=max(brr[i],brr[j]+1);}}}for(ll i=1;i<=n;i++)//最长不上升子序列{brr[i]=1;for(ll j=1;j<i;j++){if(arr[i]<=arr[j]){brr[i]=max(brr[i],brr[j]+1);}}}for(ll i=1;i<=n;i++)//最长不下降子序列{brr[i]=1;for(ll j=1;j<i;j++){if(arr[i]>=arr[j]){brr[i]=max(brr[i],brr[j]+1);}}}
}二分思想
用于处理大型数据
先来看例子
3 1 2 1 8 5 6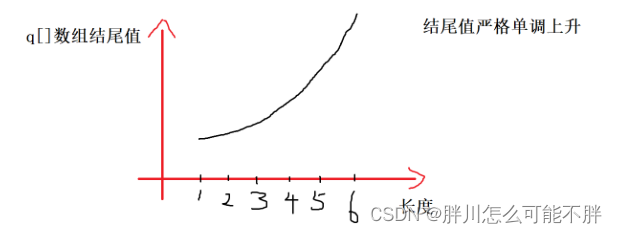
1、如图所示,可以发现找到长度为1的上升子序列,若后面的数能接到3的后面,那么一定能接到1的后面,因为1比3更好,扩展度高
2、使用q[]存储所有不同长度的上升子序列结尾的最小值
3、进来一个数arr[i]时,通过二分在q[]中找到最大的小于arri的数,就能够将arri接到该数的后面,即更新q[r + 1] = arr[i]
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
//#include<unordered_map>
#include<map>
#include<cstring>
//#include <unordered_set>
#include<queue>
#include<set>
#include<stdlib.h>
#define dbug cout<<"hear!"<<endl;
#define rep(a,b,c) for(ll a=b;a<=c;a++)
#define per(a,b,c) for(ll a=b;a>=c;a--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
#define endl "\n"
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
typedef pair<long double,long double> PDD;
const int N = 4e5 + 5;
const int INF = 0x3f3f3f3f;
//const ll LINF=LLONG_MAX;
// ll gcdd(ll a, ll b)
// {
// while(b^=a^=b^=a%=b);
// return a;
// }
// void add(ll a,ll w)
// {
// noda[++idx].b=w;
// noda[idx].ne=h[a];
// h[a]=idx;
// }ll h[N],idx;
const ll mod =1000000007;
ll t, n,a,b,c,d, m, x,y, k, cnt, ans, ant, sum,q,p,num;
ll arr[N],brr[N], crr[N];
bool book[N];int main()
{IOS;cin>>n;for(ll i=0;i<n;i++){cin>>arr[i];}/最长上升子序列ans=0;brr[0]=-2e9;for(ll i=0;i<n;i++){//手写二分ll l=0,r=ans;while(l<r){ll mid=l+r+1>>1;if(brr[mid]<arr[i]){l=mid;}else{r=mid-1;}}brr[r+1]=arr[i];ans=max(ans,r+1);/调用二分函数cnt=lower_bound(brr,brr+ans+1,arr[i])-brr;ans=max(ans,cnt);brr[cnt]=arr[i];}cout<<ans;/最长下降子序列ans=0;brr[0]=-2e9;for(ll i=0;i<n;i++){//手写二分ll l=0,r=ans;while(l<r){ll mid=l+r+1>>1;if(brr[mid]>arr[i]){l=mid;}else{r=mid-1;}}brr[r+1]=arr[i];ans=max(ans,r+1);}cout<<ans;/最长不下降序列ans=0;brr[0]=-2e9;for(ll i=0;i<n;i++){//手写二分ll l=0,r=ans;while(l<r){ll mid=l+r+1>>1;if(brr[mid]<=arr[i]){l=mid;}else{r=mid-1;}}brr[r+1]=arr[i];ans=max(ans,r+1);}cout<<ans;/最长不上升子序列ans=0;brr[0]=-2e9;for(ll i=0;i<n;i++){//手写二分ll l=0,r=ans;while(l<r){ll mid=l+r+1>>1;if(brr[mid]>=arr[i]){l=mid;}else{r=mid-1;}}brr[r+1]=arr[i];ans=max(ans,r+1);}cout<<ans;
}浅浅举个例子
拦截导弹
某国为了防御敌国的导弹袭击,开发出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭,并观测到导弹依次飞来的高度,请计算这套系统最多能拦截多少导弹。拦截来袭导弹时,必须按来袭导弹袭击的时间顺序,不允许先拦截后面的导弹,再拦截前面的导弹。
Input
输入有两行,
第一行,输入雷达捕捉到的敌国导弹的数量k(k<=25),
第二行,输入k个正整数,表示k枚导弹的高度,按来袭导弹的袭击时间顺序给出,以空格分隔。
Output
输出只有一行,包含一个整数,表示最多能拦截多少枚导弹。
Sample
| Inputcopy | Outputcopy |
|---|---|
8 300 207 155 300 299 170 158 65 | 6 |
注意细节:后一发的导弹高度不能高于前一段也就是严格小于,所以就是求最大下降子序列
#include<iostream>
#include<cmath>
#include<cstring>
#include<cstdio>
#include<stack>
#include<string>
#include<algorithm>
//#include<unordered_map>
#include<map>
#include<cstring>
//#include <unordered_set>
#include<queue>
#include<set>
#include<stdlib.h>
#define dbug cout<<"hear!"<<endl;
#define rep(a,b,c) for(ll a=b;a<=c;a++)
#define per(a,b,c) for(ll a=b;a>=c;a--)
#define no cout<<"NO"<<endl;
#define yes cout<<"YES"<<endl;
#define endl "\n"
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
//priority_queue<int,vector<int>,greater<int> >q;
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<ll, ll> PII;
typedef pair<long double,long double> PDD;
const int N = 4e5 + 5;
const int INF = 0x3f3f3f3f;
//const ll LINF=LLONG_MAX;
// ll gcdd(ll a, ll b)
// {
// while(b^=a^=b^=a%=b);
// return a;
// }
// void add(ll a,ll w)
// {
// noda[++idx].b=w;
// noda[idx].ne=h[a];
// h[a]=idx;
// }ll h[N],idx;
const ll mod =1000000007;
ll t, n,a,b,c,d, m, x,y, k, cnt, ans, ant, sum,q,p,num;
ll arr[N],brr[N], crr[N];
bool book[N];int main()
{IOS;cin>>n;for(ll i=0;i<n;i++){cin>>arr[i];}rep(i,1,n){brr[i]=1;rep(j,1,i){if(arr[i]<arr[j]){brr[i]=max(brr[i],brr[j]+1);}}}ans=0;rep(i,1,n){// cout<<brr[i]<<' ';ans=max(ans,brr[i]);}
cout<<ans;
}











![[Python]pip查找包的历史版本](https://img-blog.csdnimg.cn/277106b90e90432aaca7b748ea52a64c.png)


