1.最长公共子序列的长度

题目：对于两个字符串，请设计一个高效算法，求他们的最长公共子序列的长度，这里的最长公共子序列定义为有两个序列U1,U2,U3...Un和V1,V2,V3...Vn,其中Ui&ltUi+1，Vi&ltVi+1。且A[Ui] == B[Vi]。

给定两个字符串A和B，同时给定两个串的长度n和m，请返回最长公共子序列的长度。保证两串长度均小于等于300。

样例：

"1A2C3D4B56",10,"B1D23CA45B6A",12
返回：

解析：求不连续的公共子序列的长度,O(n2)

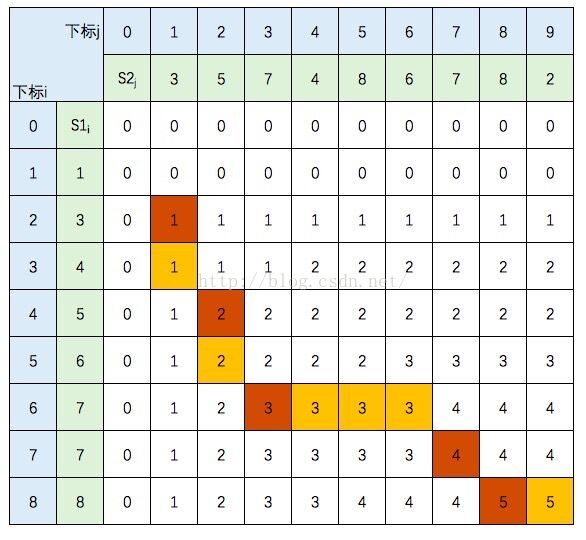
dp[ i ][ j ] 为A的0 - i 的子串与B的0 - i 的子串的最大公共子序列长度

// 最长公共子序列，动规，O(n2)public static int findLCS(String A, String B) {int n = A.length();int m = B.length();int[][] dp = new int[n + 1][m + 1];for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (A.charAt(i) == B.charAt(j)) {dp[i + 1][j + 1] = dp[i][j] + 1;} else {dp[i + 1][j + 1] = Math.max(dp[i][j + 1], dp[i + 1][j]);}}}return dp[n][m];}

2.打印最长公共子序列

同上，回溯打印。

	// 打印最长公共子序列，动规，O(n2)public static String findLCS2(String A, String B) {int n = A.length();int m = B.length();int[] path = new int[n];StringBuffer ret = new StringBuffer();int[][] dp = new int[n + 1][m + 1];for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (A.charAt(i) == B.charAt(j)) {dp[i + 1][j + 1] = dp[i][j] + 1;} else {dp[i + 1][j + 1] = Math.max(dp[i][j + 1], dp[i + 1][j]);}}}int i = n;int j = m;int k = 0;while (dp[i][j] > 0) {if (dp[i][j] == dp[i - 1][j])i--;else if (dp[i][j] == dp[i][j - 1])j--;else {path[k++] = i - 1;i--;j--;}}for (i = k - 1; i >= 0; i--)ret.append(A.charAt(path[i]));return ret.toString();}

3.最长公共子串的长度

题目：对于两个字符串，请设计一个时间复杂度为O(m*n)的算法(这里的m和n为两串的长度)，求出两串的最长公共子串的长度。这里的最长公共子串的定义为两个序列U1,U2,..Un和V1,V2,...Vn，其中Ui + 1 == Ui+1,Vi + 1 == Vi+1，同时Ui == Vi。

给定两个字符串A和B，同时给定两串的长度n和m。

样例：

"1AB2345CD",9,"12345EF",7

返回：4

解析：求连续的公共子串的长度，O(n2)

dp[ i ][ j ] 为A的以 i 结尾的和子串与B的以 j 结尾的子串最大公共子串长度

// 最长公共子串，动规，O(n2)public int findLongest(String A, String B) {int n = A.length();int m = B.length();int[][] dp = new int[n][m];int max = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (A.charAt(i) == B.charAt(j)) {if (i == 0 || j == 0) {dp[i][j] = 1; // if(arrA[i]==arrB[0])dp[i][0]=1;if(arrB[j]==arrA[0])dp[0][j]=1;} else {dp[i][j] = dp[i - 1][j - 1] + 1;}max = Math.max(dp[i][j], max);}}}return max;}

4.打印最长公共子串

例子同上，稍作修改便可：记录最大连续结尾位置

// 打印最长公共子串，动规，O(n2)public static String findLongest2(String A, String B) {int n = A.length();int m = B.length();int index_i = 0;// 记录最长公共子串结尾位置int[][] dp = new int[n][m];int max = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (A.charAt(i) == B.charAt(j)) {if (i == 0 || j == 0) {dp[i][j] = 1; // if(arrA[i]==arrB[0])dp[i][0]=1;if(arrB[j]==arrA[0])dp[0][j]=1;} else {dp[i][j] = dp[i - 1][j - 1] + 1;}if (max < dp[i][j]) {max = dp[i][j];index_i = i;}}}}String result = A.substring(index_i - max + 1, index_i + 1);return result;}

5.A串变为B串所需要的最少代价

题目：对于两个字符串A和B，我们需要进行插入、删除和修改操作将A串变为B串，定义c0，c1，c2分别为三种操作的代价，请设计一个高效算法，求出将A串变为B串所需要的最少代价。
给定两个字符串A和B，及它们的长度和三种操作代价，请返回将A串变为B串所需要的最小代价。保证两串长度均小于等于300，且三种代价值均小于等于100。
样例：
"abc",3,"adc",3,5,3,100
返回：8

解析：

dp[i][j]表示A[0..i-1]变到B[0..j-1]需要的最小代价

长度为i的A修改为长度为j的B可以分为：
1、长度为i的A修改为长度为j-1的B，然后插入j位置的字符；
2、长度为i-1的A修改为长度为j的B，然后删除i位置的字符；
3、长度为i-1的A修改为长度为j-1的B，然后i位置的字符修改为j位置的字符。

public static int Str1ToStr2(String A, String B, int c0, int c1, int c2) {int n = A.length();int m = B.length();int[][] dp = new int[n + 1][m + 1];// dp[i][j]表示A[0..i-1]变到B[0..j-1]需要的最小代价for (int i = 1; i < n + 1; i++) {dp[i][0] = dp[i - 1][0] + c1;// 删除}for (int j = 1; j < m + 1; j++) {dp[0][j] = dp[0][j - 1] + c0;// 插入}for (int i = 1; i < n + 1; i++) {for (int j = 1; j < m + 1; j++) {if (A.charAt(i - 1) == B.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1];} else {int cost1 = dp[i][j - 1] + c0;// 插入时的代价int cost2 = dp[i - 1][j] + c1;// 删除的代价int cost3 = dp[i - 1][j - 1] + c2;// 修改的代价dp[i][j] = Math.min(cost3, Math.min(cost1, cost2));}}}return dp[n][m];}

6.由两个字符串交错组成

题目：对于三个字符串A，B，C。我们称C由A和B交错组成当且仅当C包含且仅包含A，B中所有字符，且对应的顺序不改变。请编写一个高效算法，判断C串是否由A和B交错组成。

给定三个字符串A,B和C，及他们的长度。请返回一个bool值，代表C是否由A和B交错组成。保证三个串的长度均小于等于100。

样例：

"ABC",3,"12C",3,"A12BCC",6
返回：true

解析：判断C串是否由A和B交错组成。

dp[ i ][ j ] ： A的前个字符与B的前j个字符是否与C的第前i+j-1个字符匹配

public static boolean chkMixture(String A, String B, String C) {char[] a = A.toCharArray();char[] b = B.toCharArray();char[] c = C.toCharArray();int n = a.length;int m = b.length;int v = c.length;if (m + n != v) {return false;}boolean[][] dp = new boolean[n + 1][m + 1];// A的前个字符与B的前j个字符是否与C的第前i+j-1个字符匹配dp[0][0] = true;for (int i = 1; i <= n; i++) {if (a[i - 1] == c[i - 1]) {// 只有A的字符串与C匹配dp[i][0] = true;} else {break;}}for (int j = 1; j <= m; j++) {if (b[j - 1] == c[j - 1]) {// 只有B的字符串与C匹配dp[0][j] = true;} else {break;}}for (int i = 1; i < n + 1; i++) {for (int j = 1; j < m + 1; j++) {if (dp[i - 1][j] && a[i - 1] == c[i + j - 1]) {dp[i][j] = true;continue;}if (dp[i][j - 1] && b[j - 1] == c[i + j - 1]) {dp[i][j] = true;}}}return dp[n][m];}

7.无重复字符的最长子串

题目：给定一个字符串，找出不含有重复字符的最长子串的长度。

样例：

给定 "abcabcbb" ，没有重复字符的最长子串是 "abc" ，那么长度就是3。

解析：

1. 建立一个256位大小的整型数组来代替哈希表，这样做的原因是ASCII表共能表示256个字符，记录所有字符；

2. 定义两个变量res和left，其中res用来记录最长无重复子串的长度，left指向该无重复子串左边的起始位置，遍历整个字符串，对于每一个遍历到的字符：

如果哈希表中该字符串对应的值为0，说明没有遇到过该字符，则此时计算最长无重复子串，i - left +１，其中ｉ是最长无重复子串最右边的位置，left是最左边的位置；
还有一种情况也需要计算最长无重复子串，就是当哈希表中的值小于left，这是由于此时出现过重复的字符，left的位置更新了，如果又遇到了新的字符，就要重新计算最长无重复子串。

3. 最后每次都要在哈希表中将当前字符对应的值赋值为i+1。

复杂度O(n)

public static int lengthOfLongestSubstring(String s) {char[] a = s.toCharArray();int[] m = new int[256];int res = 0, left = 0;for (int i = 0; i < s.length(); ++i) {if (m[a[i]] == 0 || m[a[i]] < left) {res = Math.max(res, i - left + 1);} else {left = m[a[i]];}m[a[i]] = i + 1;}return res;}

改进算法：

public static int lengthOfLongestSubstring2(String s) {char[] a = s.toCharArray();int[] m = new int[256];int res = 0, left = 0;for (int i = 0; i < s.length(); ++i) {left = Math.max(left, m[a[i]]);m[a[i]] = i;res = Math.max(res, i - left);}return res;}

8.求和为0的最长连续子数组

解析：

　　通过分析可知，要使其和为0，只有当1和-1的个数相等时，才会成立，但题目要求是连续子序列，所以单纯统计其1和-1个数不可取。

　　由题目中求最长连续子序列，可想到动态规划来求解，动态规划的求解既是寻找其状态转移方程和建立状态转移表的过程

　　设dp[i]为下标为i及其之前数组中所有元素的和，

如图所示，数组为1，-1，1，-1，1，-1，1，-1最后一个值为0，直接满足结果，输出8

如上图，数组1，1，-1，1，1，-1，-1，dp取值为dp[0] = dp[2] = dp[6] = 1; dp[1] = dp[3] = d[5] = 3; dp[4] = 3;

对于每个值，取最后一次出现的位置和第一次出现的位置之差，取它们的最大值，max((6 - 0),(5 - 1),(4 - 4) = 6

private static int solve(int[] numbers, int n) {int[] dp = new int[n];dp[0] = numbers[0];for (int i = 1; i < n; i++) {dp[i] = dp[i - 1] + numbers[i];}Map<Integer, Integer> dpMap = new HashMap<>();dpMap.put(0, 0);int maxLen = 0;for (int i = 0; i < n; i++) {if (!dpMap.containsKey(dp[i])) {dpMap.put(dp[i], i + 1);} else {int len = i - dpMap.get(dp[i]) + 1;maxLen = maxLen < len ? len : maxLen;}}return maxLen;}

9.和不大于M的最大连续数列。

双指针法

// 和不大于M的最大连续子数列。public static int[] findSubMaxSum(int[] numbers, int M) {int[] cumSum = new int[numbers.length + 1]; // obtain cumulative sum.int sum = 0;cumSum[0] = 0;for (int i = 0; i < numbers.length; i++) {sum += numbers[i];cumSum[i + 1] = sum;}int l = 0, r = 0; // two pointers start at tip of the array.int max = 0;int[] ids = new int[2];while (l < cumSum.length) {while (r < cumSum.length && cumSum[r] - cumSum[l] <= M) {r++;}if (cumSum[r - 1] - cumSum[l] > max) { // since cumSum[0] = 0, thus r always > 0.max = cumSum[r - 1] - cumSum[l];ids[0] = l;ids[1] = r;}l++;}System.out.println(max);return ids;}

10.至少含有K个不同数字的最小连续数列

双指针法

// 至少含有K个不同数字的最小连续子数列public static int[] findSubMinSum(int[] numbers, int K) {int[] cumSum = new int[numbers.length + 1]; // obtain cumulative sum.int sum = 0;cumSum[0] = 0;for (int i = 0; i < numbers.length; i++) {sum += numbers[i];cumSum[i] = sum;}int l = 0, r = 0; // two pointers start at tip of the array.int min = Integer.MAX_VALUE;int[] ids = new int[2];HashSet<Integer> set = new HashSet<>();while (l < numbers.length) {while (r < numbers.length && set.size() < K) {set.add(numbers[r]);r++;}int sumStart = l > 0 ? cumSum[l - 1] : 0;if (cumSum[r - 1] - sumStart < min) {min = cumSum[r - 1] - sumStart;ids[0] = l + 1;ids[1] = r;}set.remove(numbers[l]);while (l + 1 < numbers.length && numbers[l] == numbers[l + 1]) {l++;}l++;}System.out.println(min);return ids;}