最长公共子串与最长子序列

article/2025/9/28 10:06:40

一序

本文属于《图解算法》系列，上一篇整理了动态规划，动态规划可以帮助我们解决给定约束条件下找到最优解，例如背包问题。

在问题可分解为彼此独立且离散的子问题时，就可使用动态规划来解决。

在看个例子，求两个字符串的最长公共子串。

二最长公共子串

对于常见的动态规划，要回答的问题如下：

 单元格中的值是什么？

 如何将这个问题划分为子问题？

 网格的坐标轴是什么？

过程如下：

我建议自己动手参照画一下，加深自己的理解。

需要注意的一点是，这个问题的最终答案并不在最后一个单元格中！对于前面的背包问题，最终答案总是在最后的单元格中。但对于最长公共子串问题，答案为网格中最大的数字——它可能并不位于最后的单元格中。

如果还不明白，可以看看下面的代码：

/*** * @author bohu83**/
public class LCSTest2 {public static void Lcs(String stra,String strb){//填充数据使用stra = " "+stra;strb = " "+strb;int[][] arr = new int[stra.length()][strb.length()];for (int i=1;i<stra.length();i++){for(int j=1;j<strb.length();j++ ){//两个字母相同if(stra.charAt(i)== strb.charAt(j)){					  arr[i][j] = arr[i-1][j-1]+1;					}else{//两个字母不同arr[i][j] = 0;}				  }  }System.out.println(JSON.toJSON(arr));int len1= stra.length()-1;int len2= strb.length()-1;int max = 0;int index = 0;for(int i=0;i<=len1;i++){for (int j = 0; j <=len2; j++) {if(arr[i][j]>max ){max = arr[i][j];index =i;}}}//输出出来，根绝index去截取字符串System.out.println(stra.substring(index-max, index+1));}public static void main(String[] args) {Lcs("123ABCD4567","ABE12345D6");}}

这是我手画的结果，对比下程序输出：为方便对比，我稍微排序下

[[0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,1,0,0,0,0,0,0],
[0,0,0,0,0,2,0,0,0,0,0],
[0,0,0,0,0,0,3,0,0,0,0],
[0,1,0,0,0,0,0,0,0,0,0],
[0,0,2,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,0,0,0,0,0,1,0],
[0,0,0,0,0,0,0,1,0,0,0],
[0,0,0,0,0,0,0,0,2,0,0],
[0,0,0,0,0,0,0,0,0,0,1],
[0,0,0,0,0,0,0,0,0,0,0]]
123

其中123 就是结果，上面的数组就是填空的网格。

三最长公共子序列

最长公共子串问题是寻找两个或多个已知字符串最长的子串。此问题与最长公共子序列问题的区别在于子序列不必是连续的，而子串却必须是。还是上面的例子。 Lcs("123ABCD4567","ABE12345D6");

最长公共子串是：123

最长公共子序列是：123456。

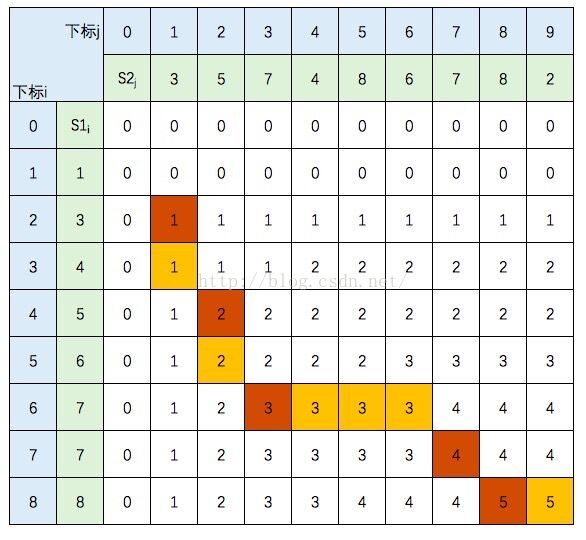
如何计算最长公共子序列呢？跟上面的最长公共子串类似。

图上提示有错，应该是最长公共子串是2，最长公共子序列是3.

手工按照规则填空的图如下：

看下代码实现。

/*** * @author bohu83* 2019-06-14*/
public class LCSTest {public static void Lcs(String stra,String strb){//填充数据使用stra = " "+stra;strb = " "+strb;int[][] arr = new int[stra.length()][strb.length()];for (int i=1;i<stra.length();i++){for(int j=1;j<strb.length();j++ ){//两个字母相同if(stra.charAt(i)== strb.charAt(j)){					  arr[i][j] = arr[i-1][j-1]+1;					}else{//两个字母不同arr[i][j] = Math.max(arr[i][j-1],arr[i-1][j]);}				  }  }System.out.println(JSON.toJSON(arr));StringBuffer sb = new StringBuffer();//作为结果int i= stra.length()-1;int j= strb.length()-1;while ( i > 0 &&  j > 0) {//边界if (stra.charAt(i) == strb.charAt(j)) {//反推公式中不相等的场景//该值一定是被选取到的，根据之前的公式，知道两条字符串的下标都前进一位sb.append(stra.charAt(i));i--;j--;} else {//对应公式中不相等的反推场景if (arr[i][j - 1] > arr[i - 1][j]) {//找大的那个方向，此处是左边大于上面，则该处的结果是来自左边j--;} else if (arr[i][j - 1] < arr[i - 1][j]) {i--;} else if (arr[i][j - 1] == arr[i - 1][j]) {//对于有分支的可能时，我们选取单方向i--;   //此结果对于结果1所选取方向，str1的下标左移一位.替换为j--，则结果对应与结果2选取的方向}}}//由于是从后往前加入字符的，需要反转才能得到正确结果System.out.println(sb.reverse().toString());}public static void main(String[] args) {Lcs("123ABCD4567","ABE12345D6");}}

这里分为两个步骤，填空相对简单，寻找过程比较复杂，要发推选取相同的字母。

输出结果：排版下结果。

[
[0,0,0,0,0,0,0,0,0,0,0],
[0,0,0,0,1,1,1,1,1,1,1],
[0,0,0,0,1,2,2,2,2,2,2],
[0,0,0,0,1,2,3,3,3,3,3],
[0,1,1,1,1,2,3,3,3,3,3],
[0,1,2,2,2,2,3,3,3,3,3],
[0,1,2,2,2,2,3,3,3,3,3],
[0,1,2,2,2,2,3,3,3,4,4],
[0,1,2,2,2,2,3,4,4,4,4],
[0,1,2,2,2,2,3,4,5,5,5],
[0,1,2,2,2,2,3,4,5,5,6],
[0,1,2,2,2,2,3,4,5,5,6]]

123456

这里还是有点复杂度的，需要去画图理解下。

利用动态规划求解最长公共子串，时间复杂度为O(m*n),利用广义后缀树方法会快，但是算法没这个容易理解。后面单独整理吧。