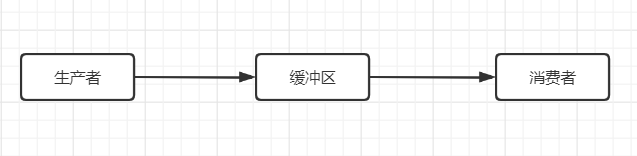
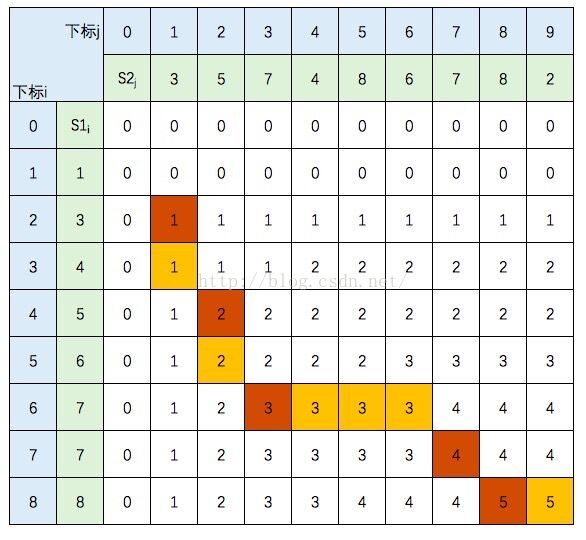
生产消费者模型中包含三个部分，生产者、消费者和交易场所。其中涉及如下的关系：

（1）生产者和生产者之间的关系：由于生产者的生产面向的都是交易场所，所以生产者之间是存在竞争关系的，就像一家超市同一件商品的不同供货商。所以生产者之间是互斥的，而互斥的关系需要通过加锁来维持正常运转。

（2）消费者和消费者之间的关系：就像去同一家超市购买同一件商品的不同消费者而言，消费者之间也是存在竞争关系的。（无论是生产者之间还是消费者之间，需求的都是同样的资源，所以相互之间是一定存在竞争关系的）

（3）生产者和消费者之间的关系：生产者和消费者之间既存在同步关系也存在互斥关系。存在互斥关系是因为无论是生产者还是消费者，都需要面向交易场所，而如果生产者和消费者同时对交易场所进行操作的话，难免会相互造成影响，所以二者之间存在互斥关系。不过，为了维持生产消费者模型的正常运转，生产者和消费者之间也要存在同步关系，亦即相互之间根据彼此的状况对自身进行调整，否则，会出现供大于求的情况，导致冗余问题，或者供小于求的情况，导致饥饿问题。因此，生产者和消费者在互斥的基础上也要维持同步。其中互斥关系一般借助互斥锁来实现，而同步关系一般借助条件变量来实现。

交易场所一般指内存中的一段缓冲区，具有临时保存数据的功能。

 

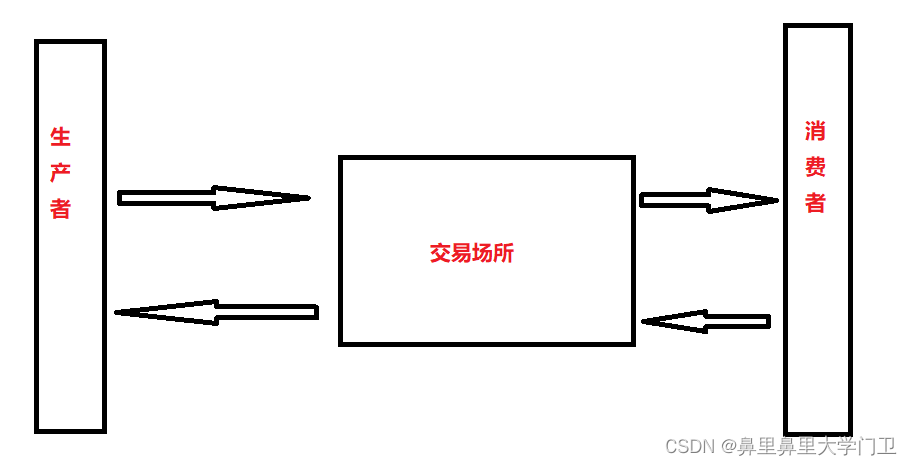
生产消费者模型的意义：

（1)解耦：对于一个普通的函数而言，其按部就班的从上到下运行，不过当涉及一个函数调用的时候，从调用这个函数、把参数传递给这个函数、再到这个函数把运行结果返回给主程序，在这段过程中，主程序是什么都不能做的，只能卡在那里，等待处理结果，这就会浪费很多时间。也就是说此时，数据的发送方（主程序）和数据的处理方（被调用的函数）之间是紧耦合的。

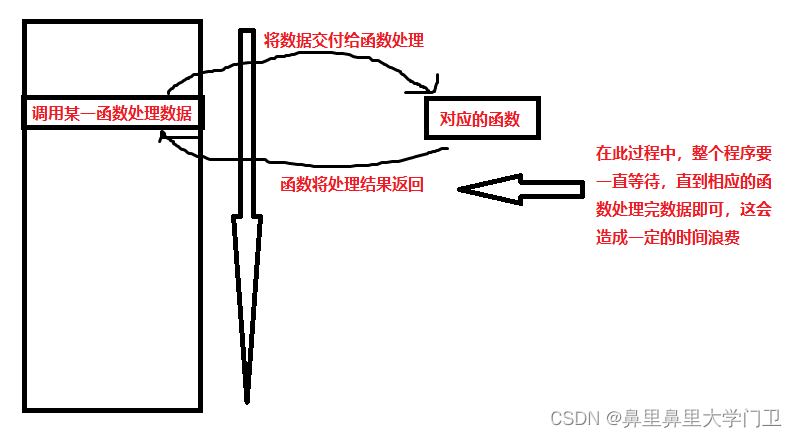
 相比之下，如果使用生产消费者模型，由于交易场所（缓冲区）的存在，数据的生产者（主程序）可以直接将生产出的数据放到交易场所中，在这之后有关这些数据的具体细节就不需要生产者关注了，可以继续去运行。消费者也同理，也就是由于生产消费者模型的存在，借助缓冲区，让生产者和消费者之间实现了解耦，不需要相互之间等待，影响效率。

（2）支持忙闲不均：由于缓冲区的存在，使得哪怕数据的生产和消费速率不一致，整个模型也可以正常工作。当然，缓冲区的大小是有限的，所以生产者和消费者也要随时借助条件变量来调整自己的工作状态。