最长公共子序列:
链接:https://www.nowcoder.com/questionTerminal/9ae56e5bdf4f480387df781671db5172
题目:
我们有两个字符串m和n,如果它们的子串a和b内容相同,则称a和b是m和n的公共子序列。子串中的字符不一定在原字符串中连续。
例如字符串“abcfbc”和“abfcab”,其中“abc”同时出现在两个字符串中,因此“abc”是它们的公共子序列。此外,“ab”、“af”等都是它们的字串。
现在给你两个任意字符串(不包含空格),请帮忙计算它们的最长公共子序列的长度。
题解:给定我们两个字符串求解最长的公共子序列,并且公共串是可以不连续,也就是说只要要找两个字符串公共子串的最长长度;
如果采取暴力方法,我们可以分别求出字符串m的所有子串存于set容器中,在求出字符串n的所有子串,进行查询,找出最长的公共子串,但是这种方法的效率极低。
所以我们将回到本篇的标题:动态规划
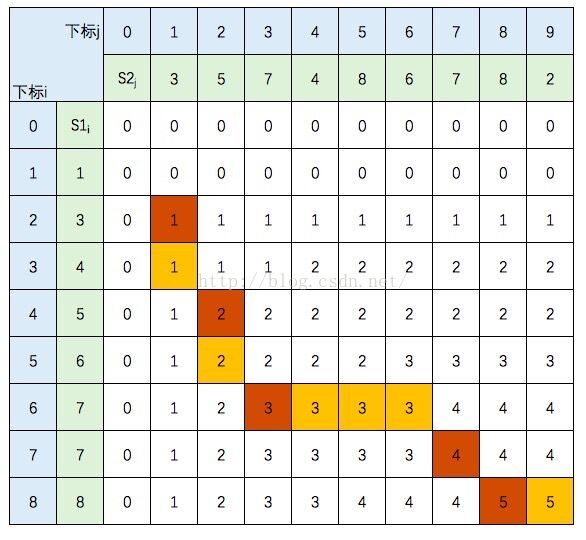
1.状态定义(给定一个二维数组,数组的行代表字符m,列代表字符n)
那我们在二维数组[ i ][ j ]的位置表示字符串m的前i个字符与字符串n的前j个字符的最长公共子串的长度
2.状态转移:
根据状态定义,我们知道在一个判断中无非有两种情况:第i个字符与第j个字符相同;第i个字符与第j个字符不同;
- 第i个字符与第j个字符相同,那么[ i ][ j ]的位置可存储的数据就有两个选择,一个是[ i ][ j ],另一个是[ i-1 ][ j-1 ]+1 即表示字符串m的前i-1个字符与字符串n的前j-1个字符的最长公共子串的长度+当前位置的一个相同字符。故这种情况下状态转移方程为dp[i][j]=max(dp[i-1][j-1]+1,dp[i-1][j-1]);
- 第i个字符与第j个字符不同,我们就可以保存之前的公共子序列的最大长度,那之前的位置有谁呢?即当前位置的上面位置和左边位置即[i-1][j] ; [i][j-1]
- 故这种情况下状态转移方程为dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
3.结果:
顾名思义:结果将保存在二维数字最右下角
代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
int main()
{string str1,str2;while(cin>>str1>>str2){int len1=str1.size();int len2=str2.size();vector<vector<int>> dp(len1+1,vector<int>(len2+1,0));//str1的前i位和str2的前j位所拥有的最大的公共字符串的个数for(int i=0;i<len1;++i){for(int j=0;j<len2;++j){if(str1[i]==str2[j]){dp[i+1][j+1]=max(dp[i][j]+1,dp[i+1][j+1]);}else{dp[i+1][j+1]=max(dp[i+1][j],dp[i][j+1]);}}}cout<<dp[len1][len2]<<endl;}return 0;
}