文章目录

文章目录
一、基本知识
二、最长上升子序列
- 1.朴素版
- 2.二分版
三、最长公共子序列

一、基本知识

1.子串和子序列的区别： 子串必须连续,子序列可以不连续。

2.最长上升子序列(LIS)： 是指一个序列中最长的单调递增的子序列。

3.最长公共子序列(LCS)： 是一个在一个序列集合中（通常为两个序列）用来查找所有序列中最长子序列的问题。一个数列，如果分别是两个或多个已知数列的子序列，且是所有符合此条件序列中最长的，则称为已知序列的最长公共子序列。

二、最长上升子序列

1.朴素版

题目: AcWing 895. 最长上升子序列

给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

数据范围:

1≤N≤1000，
−10 ^9 ≤ 数列中的数 ≤ 10 ^9

解析:

(1) f[N]:所有以第i个数结尾的上升子序列

(2) f[i]=max(f[j]+1),j=0,1,2…i-1

代码:

#include<iostream>
using namespace std;
const int N=1010;
int n,a[N],ans;
int f[N];//所有以第i个数结尾的上升子序列 
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}for(int i=1;i<=n;i++){f[i]=1;// i本身 //f[i]=max(f[j]+1),j=0,1,2...i-1for(int j=1;j<=i;j++){if(a[i]>a[j]){f[i]=max(f[i],f[j]+1);}}}for(int i=1;i<=n;i++){ans=max(f[i],ans);}printf("%d\n",ans);return 0;
}

2.二分版

题目: AcWing 896. 最长上升子序列 II
给定一个长度为 N 的数列，求数值严格单调递增的子序列的长度最长是多少。

数据范围:
1≤N≤100000，
−10 ^9≤数列中的数≤10 ^9

解析:

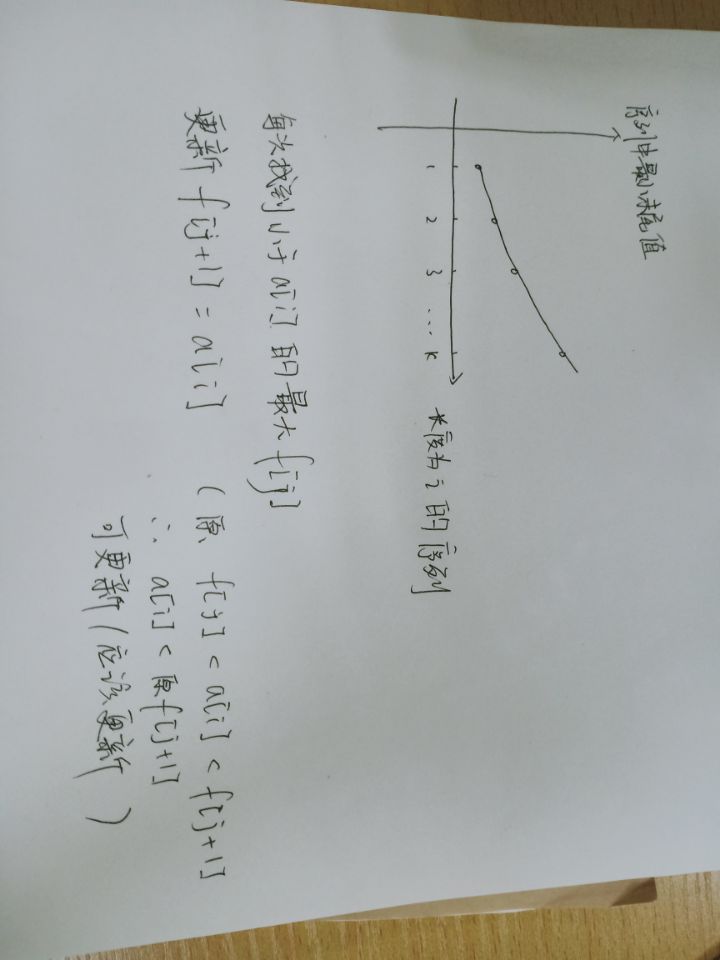
在这里插入图片描述

代码:

#include<iostream>
using namespace std;
const int N=100010;
int a[N],n;
int q[N];
//q[i]=j:长度为i,子序列末尾最小值为j 
int main()
{scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}int len=0;for(int i=1;i<=n;i++){int l=0,r=len;//在子序列中二分找到小于a[i]的最大值while(l<r){int mid=l+r+1>>1;if(q[mid]<a[i]){l=mid;}else{r=mid-1;}}len=max(len,r+1);//更新q[r+1] q[r+1]=a[i];}printf("%d\n",len);return 0;
}

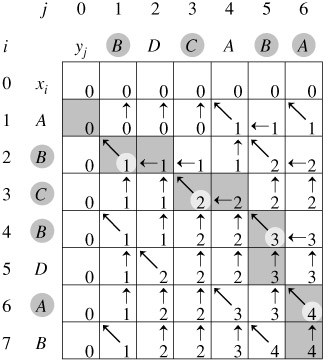
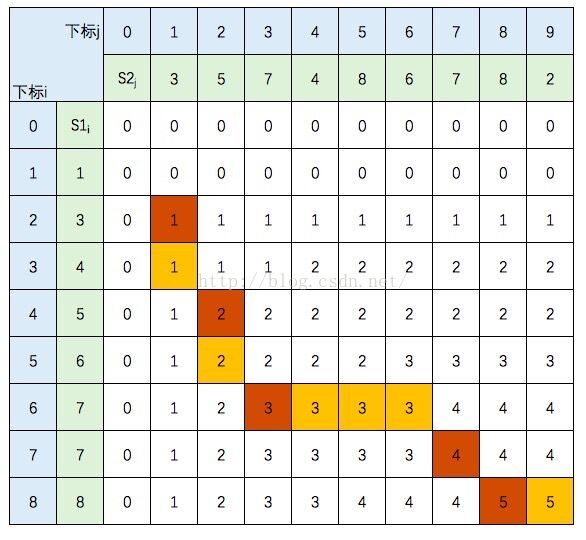
三、最长公共子序列

题目: AcWing 897. 最长公共子序列
给定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B 的子序列的字符串长度最长是多少。

数据范围:
1≤N,M≤1000

解析:
(1)f [ i , j ]： 所有A[1 ~ i]与B[1 ~ j]的公共子序列的集合
(2)四类状态：
1 .f[i-1,j-1]： a[i]、b[j]都不包含
2 .f[i-1,j]： 不包含a[i]，包含b[j]
3 .f[i,j-1]： 包含a[i]，不包含b[j]
4 .f[i-1,j-1]+1： a[i]、b[j]都包含

因为状态2、3包含状态1，划掉1.

代码:

#include<iostream>
using namespace std;
const int N=1010;
char a[N],b[N];
int n,m;
//所有A[1~i]与B[1~j]的公共子序列的集合 
int f[N][N];
int main()
{scanf("%d%d",&n,&m);scanf("%s%s",a+1,b+1);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){//f[i-1,j-1]包含在f[i-1,j]和f[i,j-1]中 f[i][j]=max(f[i-1][j],f[i][j-1]);if(a[i]==b[j]){f[i][j]=max(f[i][j],f[i-1][j-1]+1);}}}cout<<f[n][m]<<endl;return 0;
}