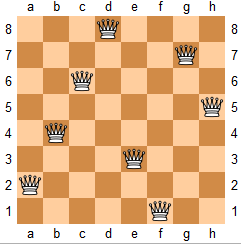
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
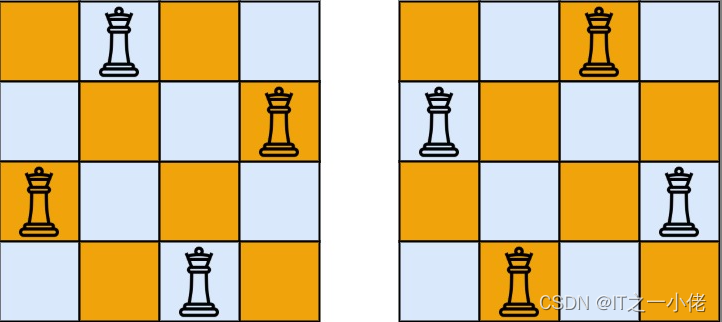
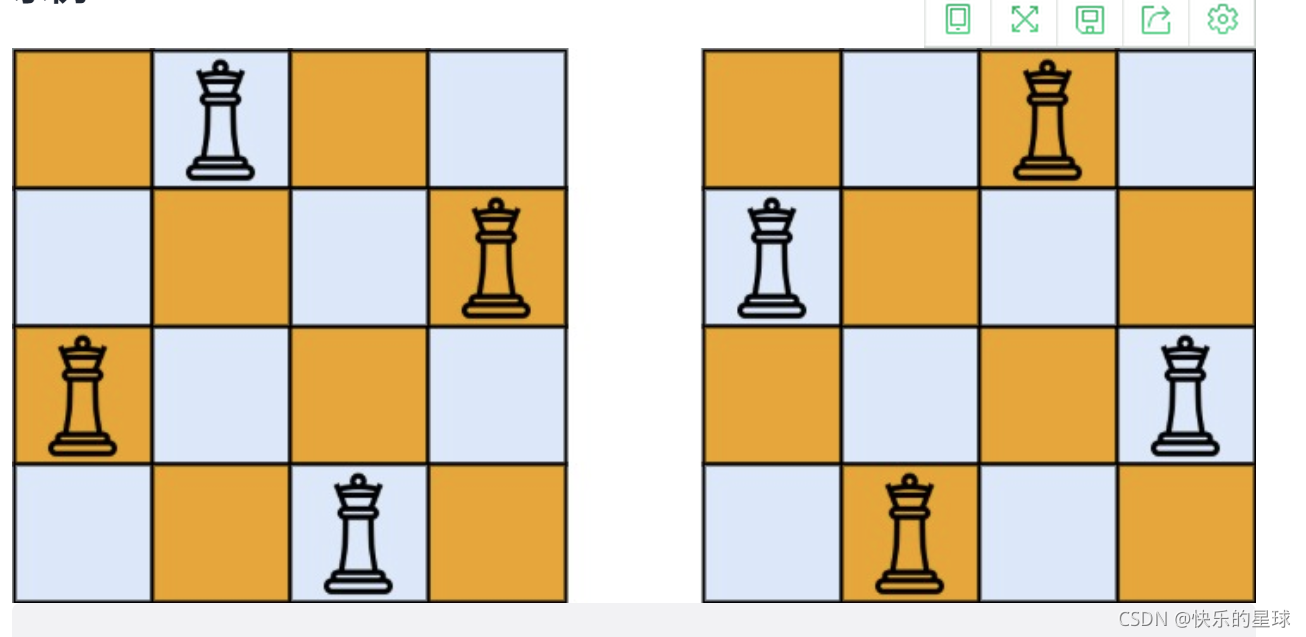
输入:n = 4
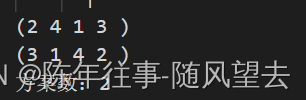
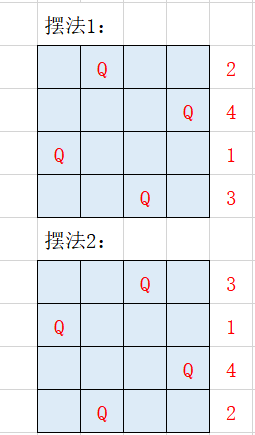
输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
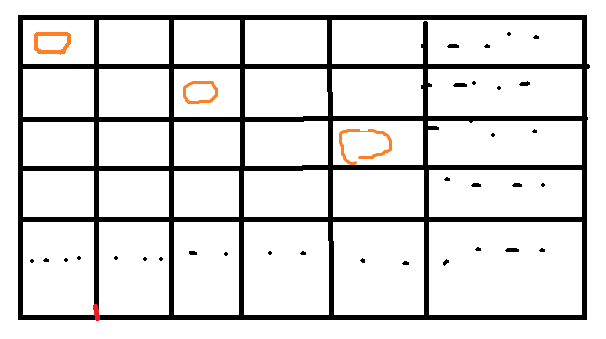
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[["Q"]]
题目解读:
「N 皇后问题」研究的是如何将 N 个皇后放置在N×N 的棋盘上,并且使皇后彼此之间不能相互攻击。
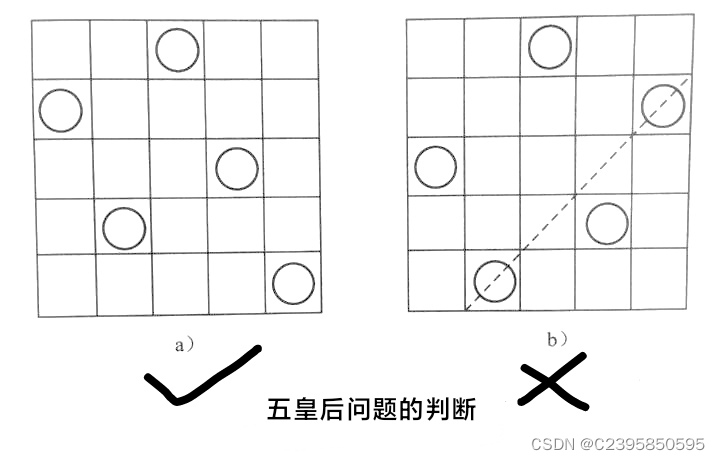
皇后的走法是:可以横直斜走,格数不限。因此要求皇后彼此之间不能相互攻击,等价于要求任何两个皇后都不能在同一行、同一列以及同一条斜线上。
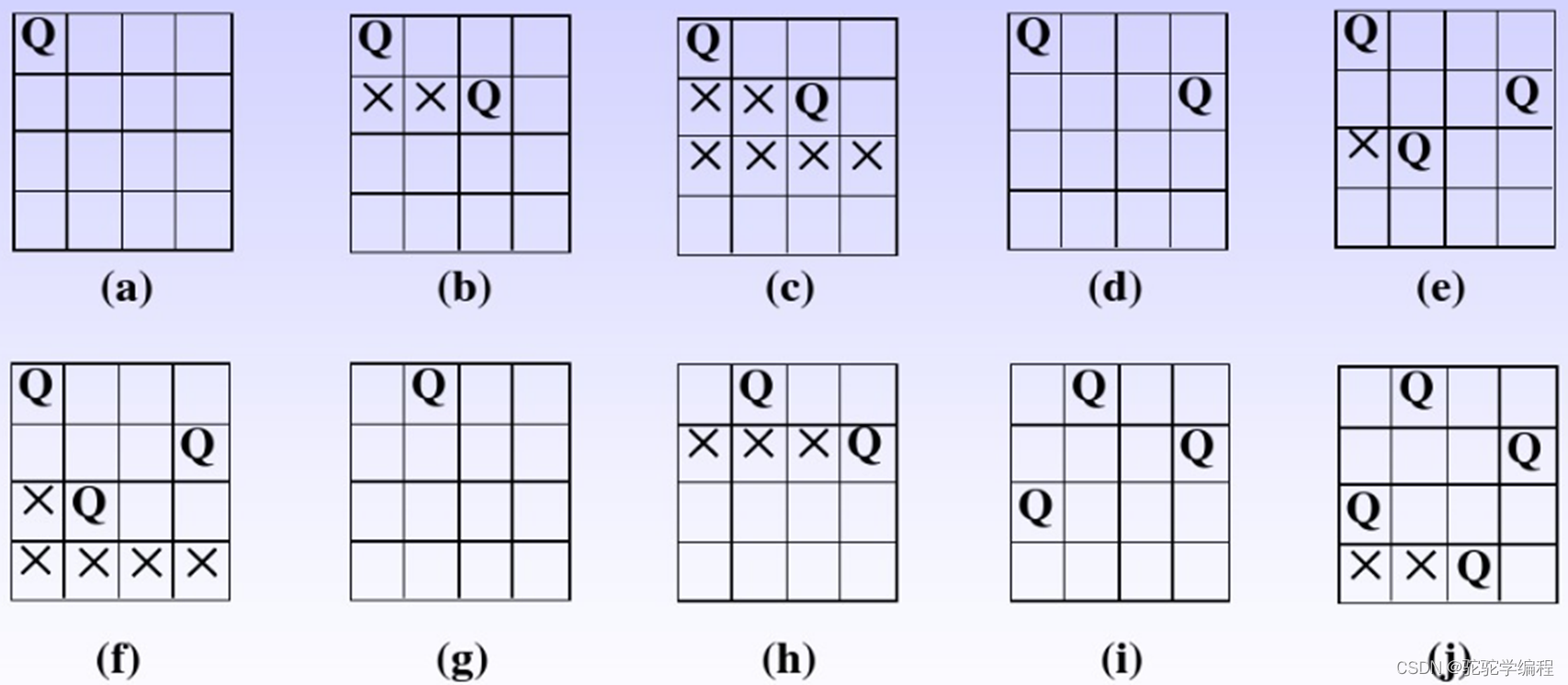
直观的做法是暴力枚举将 N 个皇后放置在N×N 的棋盘上的所有可能的情况,并对每一种情况判断是否满足皇后彼此之间不相互攻击。暴力枚举的时间复杂度是非常高的,因此必须利用限制条件加以优化。
显然,每个皇后必须位于不同行和不同列,因此将 N 个皇后放置在N×N 的棋盘上,一定是每一行有且仅有一个皇后,每一列有且仅有一个皇后,且任何两个皇后都不能在同一条斜线上。基于上述发现,可以通过回溯的方式寻找可能的解。
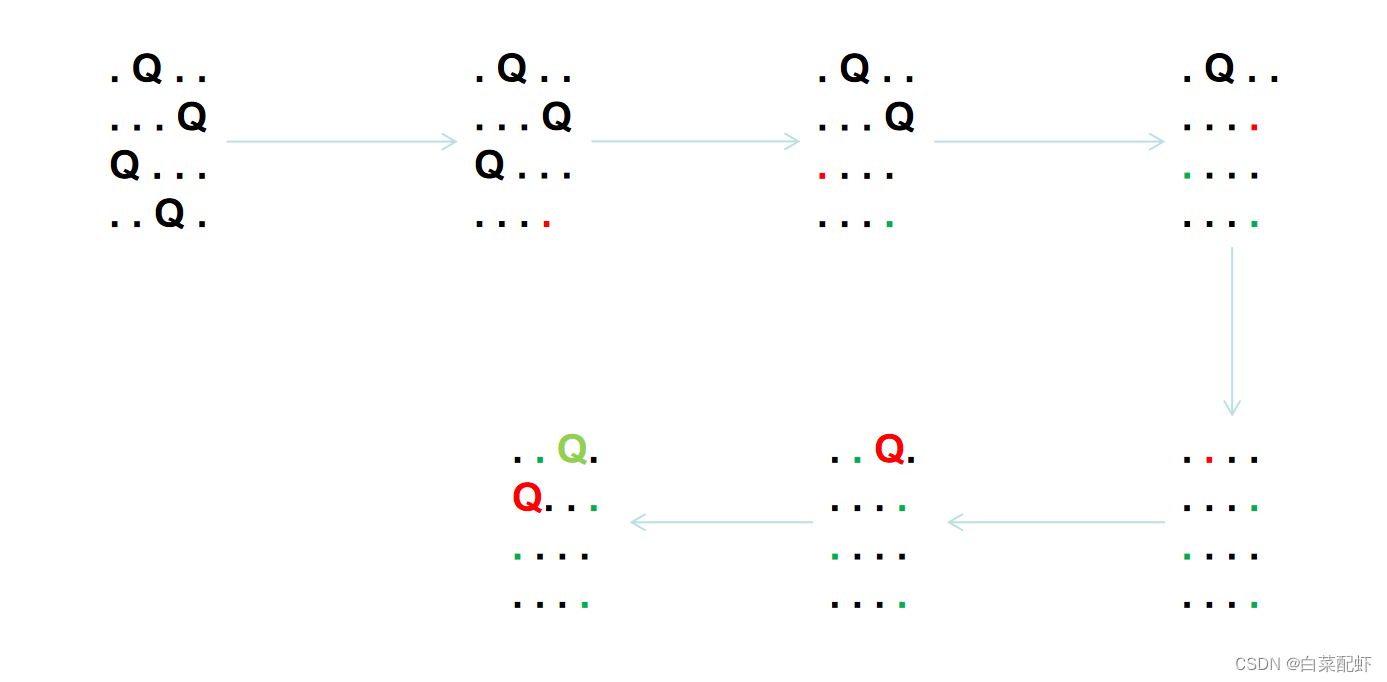
回溯的具体做法是:使用一个数组记录每行放置的皇后的列下标,依次在每一行放置一个皇后。每次新放置的皇后都不能和已经放置的皇后之间有攻击:即新放置的皇后不能和任何一个已经放置的皇后在同一列以及同一条斜线上,并更新数组中的当前行的皇后列下标。当 N 个皇后都放置完毕,则找到一个可能的解。当找到一个可能的解之后,将数组转换成表示棋盘状态的列表,并将该棋盘状态的列表加入返回列表。
由于每个皇后必须位于不同列,因此已经放置的皇后所在的列不能放置别的皇后。第一个皇后有 NN列可以选择,第二个皇后最多有N−1 列可以选择,第三个皇后最多有 N−2 列可以选择(如果考虑到不能在同一条斜线上,可能的选择数量更少),因此所有可能的情况不会超过 N! 种,遍历这些情况的时间复杂度是 O(N!)。
为了降低总时间复杂度,每次放置皇后时需要快速判断每个位置是否可以放置皇后,显然,最理想的情况是在 O(1)的时间内判断该位置所在的列和两条斜线上是否已经有皇后。
示例代码1: 【基于集合的回溯】
class Solution(object):def solveNQueens(self, n):def generate_board():board = []for i in range(n):row[queens[i]] = "Q"board.append("".join(row))row[queens[i]] = "."return boarddef backtrack(row):if row == n:board = generate_board()ret.append(board)else:for i in range(n):if i in columns or row - i in diagonal1 or row + i in diagonal2:continuequeens[row] = icolumns.add(i)diagonal1.add(row - i)diagonal2.add(row + i)backtrack(row + 1)columns.remove(i)diagonal1.remove(row - i)diagonal2.remove(row + i)ret = []queens = [-1] * nrow = ["."] * ncolumns, diagonal1, diagonal2 = set(), set(), set()backtrack(0)return retobj = Solution()
ans = obj.solveNQueens(4)
print(ans)


思路解析:
为了判断一个位置所在的列和两条斜线上是否已经有皇后,使用三个集合 columns、diagonals 1 和diagonals 2分别记录每一列以及两个方向的每条斜线上是否有皇后。
列的表示法很直观,一共有 N 列,每一列的下标范围从 0 到 N-1,使用列的下标即可明确表示每一列。如何表示两个方向的斜线呢?对于每个方向的斜线,需要找到斜线上的每个位置的行下标与列下标之间的关系。
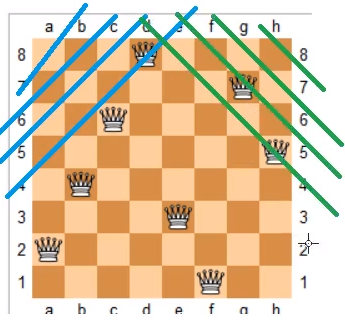
方向一的斜线为从左上到右下方向,同一条斜线上的每个位置满足行下标与列下标之差相等,例如 (0,0)和 (3,3)在同一条方向一的斜线上。因此使用行下标与列下标之差即可明确表示每一条方向一的斜线。
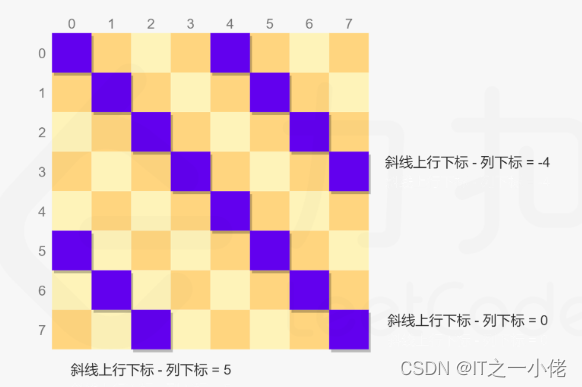
方向二的斜线为从右上到左下方向,同一条斜线上的每个位置满足行下标与列下标之和相等,例如 (3,0)和 (1,2)在同一条方向二的斜线上。因此使用行下标与列下标之和即可明确表示每一条方向二的斜线。
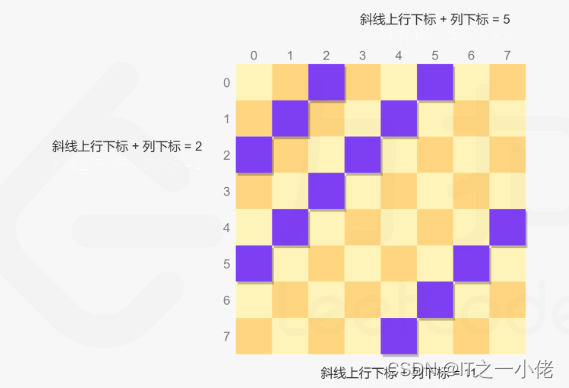
每次放置皇后时,对于每个位置判断其是否在三个集合中,如果三个集合都不包含当前位置,则当前位置是可以放置皇后的位置。
复杂度分析:
- 时间复杂度:O(N!),其中 N是皇后数量。
- 空间复杂度:O(N),其中 N是皇后数量。空间复杂度主要取决于递归调用层数、记录每行放置的皇后的列下标的数组以及三个集合,递归调用层数不会超过 N,数组的长度为 N,每个集合的元素个数都不会超过 N。
示例代码2:【这种方法看起来稍微好理解一下,相比上面比较耗时】
class Solution(object):def solveNQueens(self, n):if not n:return []board = [['.'] * n for _ in range(n)]res = []def is_valid(board, row, col):# 判断同一列是否冲突for i in range(len(board)):if board[i][col] == "Q":return False# 判断左上角是否冲突i = row - 1j = col - 1while i >= 0 and j >= 0:if board[i][j] == "Q":return Falsei -= 1j -= 1# 判断又上角是否冲突i = row - 1j = col + 1while i >= 0 and j < len(board):if board[i][j] == "Q":return Falsei -= 1j += 1return Truedef backtrace(board, row, n):# 如果走到最后一行,说明已经找到一个解if row == n:tmp_res = []for tmp in board:tmp_str = "".join(tmp)tmp_res.append(tmp_str)res.append(tmp_res)for col in range(n):if not is_valid(board, row, col):continueboard[row][col] = "Q"backtrace(board, row + 1, n)board[row][col] = "."backtrace(board, 0, n)return resobj = Solution()
ans = obj.solveNQueens(4)
print(ans)


思路解析:
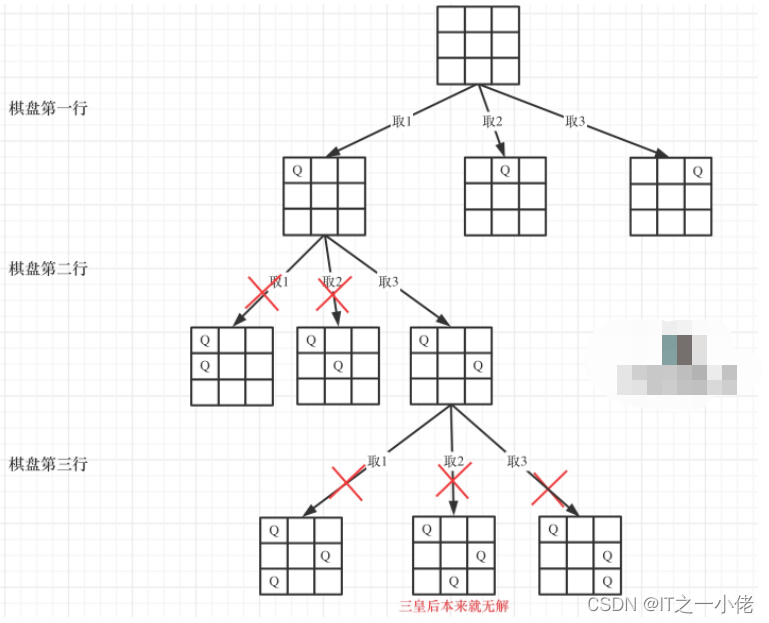
- 单层搜索的逻辑
递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。
每次都是要从新的一行的起始位置开始搜,所以都是从0开始。
- 验证***是否合法
按照如下标准去重:
- 不能同行
- 不能同列
- 不能同斜线 (45度和135度角)