一、题目描述

N 皇后问题是指在 n * n 的棋盘上要摆 n 个皇后，
要求：任何两个皇后不同行，不同列也不在同一条斜线上，
求给一个整数 n ，返回 n 皇后的摆法数。

数据范围: 1 ≤ n ≤ 9

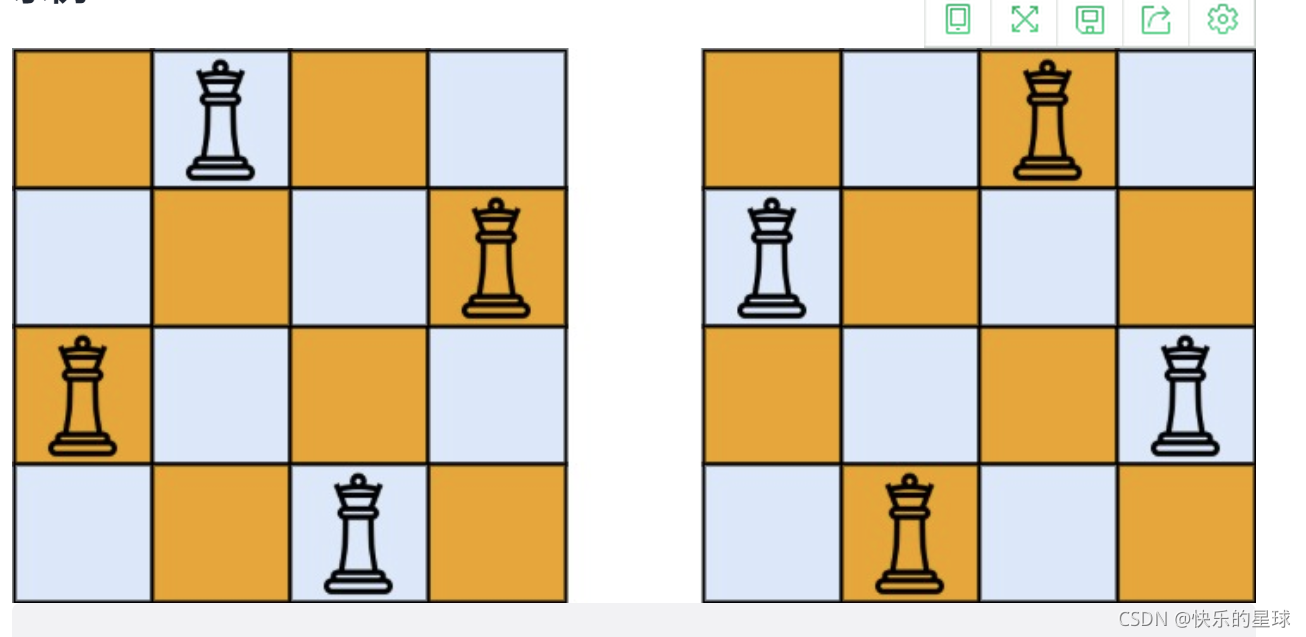
例如当输入4时，对应的返回值为2，对应的两种四皇后摆位如下图所示：

二、题目解析

（1）思考一(集合+回溯)

变量罗列：

• i：行号
• j：列号
• set1：保存已经被占用的列
• set2：保存已经被占用的左斜线（横纵坐标相加确定一条左斜线）
• set3：保存已经被占用的右斜线（横纵坐标相减确定一条右斜线）
• result ：摆放数

思路分析：

将从第 0 行开始放皇后，放成功后再放第 1 行，保证皇后们都不在同一行上

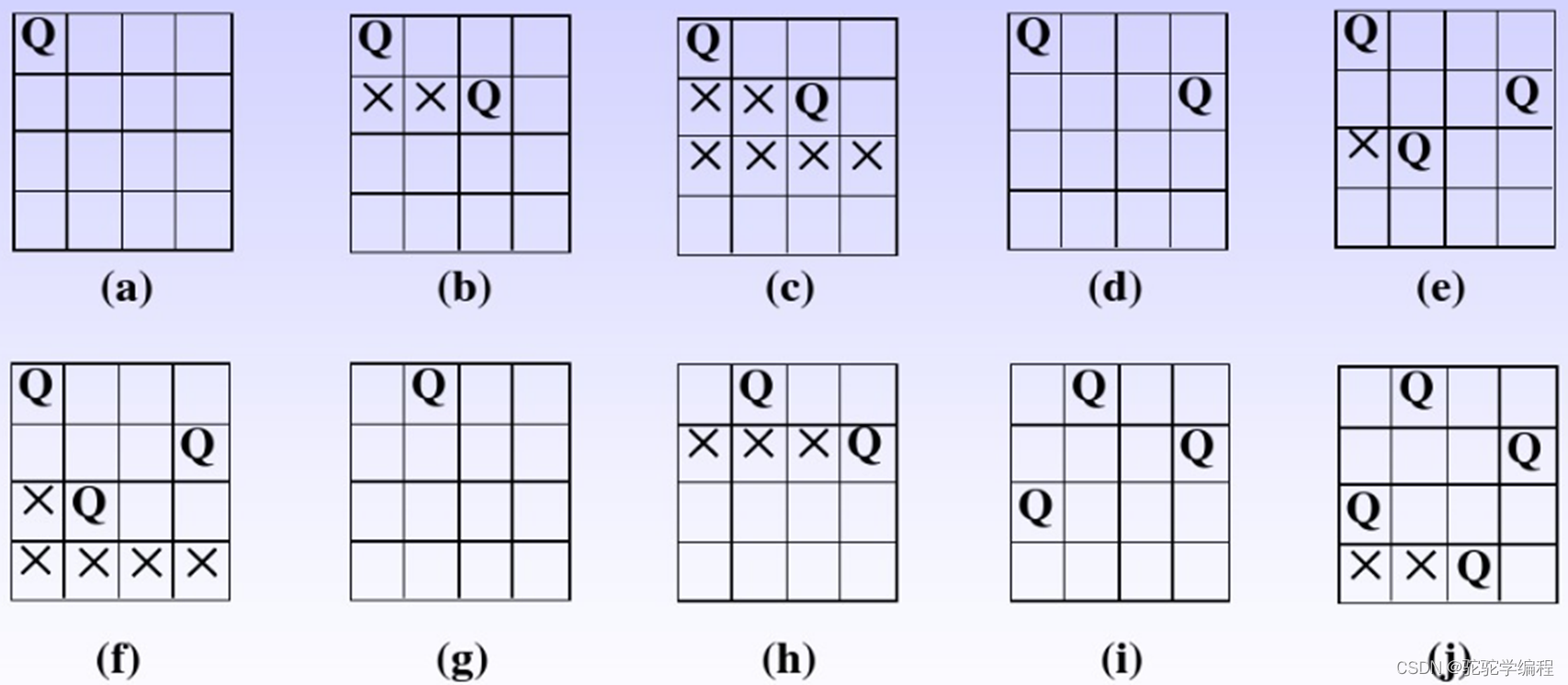
在第 i 行寻找放皇后的位置时，将会依次从第 0 列尝试到第 n-1 列，尝试着将皇后放在坐标 （i，j）上，如果 set1 中没有包含 j，set2 中没有包含 i+j，set3 中没有包含 i-j，皇后放置成功

第 i 行的皇后放成功后，就可以开始放第 i+1 行的皇后，直到 i == n ,棋盘上成功多出了一种摆放法，result 加一

返回后就回溯，撤掉刚才摆放好的皇后，尝试下一列，没有下一列说明当前方法执行完毕，返回了

代码展示：

public class Solution {public HashSet<Integer> set1 = new HashSet<>();//列public HashSet<Integer> set2 = new HashSet<>();//正斜线public HashSet<Integer> set3 = new HashSet<>();//反斜线public int result = 0;public int Nqueen (int n) {func(0,n);//表示从第0行开始放，一共有n行return result;}public void func(int i,int n) {if(i == n) {//放好了result++;return;}//在第i行中依次找到一个合适的列放皇后for(int j = 0;j < n;j ++) {if(set1.contains(j) || set2.contains(i+j) || set3.contains(i-j)) {continue;//都是不符合条件的}set1.add(j);set2.add(i+j);set3.add(i-j);//放好了，尝试下一行func(i+1,n);//恢复原样set1.remove(j);set2.remove(i+j);set3.remove(i-j);}}
}

（2）思考二(数组+深度递归)

变量罗列：

• i：行号
• j：列号
• board数组：board[i] 表示第 i 行放皇后的列号
• result ：摆放数

思路分析：

和思路一的区别在于使用一个数组代替三个 set 集合

在第 i 行放置皇后时，第 0 行到第 i-1 行都放好皇后，board[0~i-1] 上的值都有效，符合题目的限定条件

在判断坐标（i，j）位置是否能够放皇后时，如果board[k] (0 ≤ k ≤ i-1) 的值等于 j ，说明和第 k 行的皇后重行。如果 board[k] 和 j 差的绝对值等于 k 和 i 差的绝对值，说明坐标 （i，j）和坐标（k，board[k]）相连后和水平呈45度角，即在同一条斜线上（包含左斜线和右斜线）

将第 i 行上所有可以放置皇后的列所包含的摆法数累加，并返回

代码展示：

public class Solution1 {public int Nqueen (int n) {int[] board = new int[n];//表示棋盘//board[i]表示第i行放皇后的列,board[2] = 3 表示第二行的皇后放在了第3列上return func(0,board,n);//表示从第0行开始往下摆皇后}public int func(int i,int[] board,int n) {//准备开始摆第i行的皇后//此时board[0~i-1]都已经有了有效值，即0~i-1行上都符合规则的放好了皇后if(i == n) {//到达终止行，即棋盘最后一行也摆好了皇后return 1;}int result = 0;//对第i行上所有符合条件可以放皇后的列的方法数进行累加for(int j = 0;j < n;j ++) {if(isOK(board,i,j)) {//可以放皇后，深度递归board[i] = j;result += func(i+1,board,n);}}return result;}//就是来验证第i行第j列是否能放皇后public boolean isOK(int[] board,int i,int j) {for(int k = 0;k < i;k ++) {if(board[k] == j || Math.abs(board[k]-j) == Math.abs(k-i)) {return false;//不符合条件}}return true;}
}

（3）思考三(位运算)

以上两种方法的时间复杂度都是 O(n!) ，空间复杂度为 O(n)，指标已经是没有办法优化了，但是可以通过位运算进行常数时间的优化，优化的目的就是省去依次判断和过去放过的皇后有重列或者重斜线的步骤

变量罗列：

• limit：表示位的限制，该值的后 n 位为 1 (若为7皇后，limit为0… 0111 1111)
• colLim：表示列的限制，1表示已经放了皇后，0表示没有放过皇后
• leftLim：表示左斜线的限制，1表示已经放了皇后，0表示没有放过皇后
• rightLim：表示右斜线的限制，1表示已经放了皇后，0表示没有放过皇后
• pos：可以放皇后的位置，1表示可以放皇后，0表示不能放皇后
• lastOneIndex：pos最右侧的1的权值

思路分析：

以 8 皇后进行举例：

如果 colLim 后 8 位都是 1（等于limit），说明棋盘上所有的列都放上了皇后，摆放数加一

假设第 0 行的皇后放在了第 5 列

此时的 pos 值有 5 个 1，代表只有这 5 列还可以放皇后，通过 pos & (~pos + 1) 就可以求的最右侧的 1的权值（lastOneIndex），将皇后放到此处，pos 减去权值，直到 pos 为 0 说明 5 个放皇后的地方都尝试过了，累加摆放数

代码展示：

public class Solution2 {//限制：只能是1~32皇后public int Nqueen (int n) {// write code hereif (n < 1 || n > 32) {return -1;}//如果是8皇后，limit该值的后8位为1，之后所有的限制就都限制在了后8位上int limit = (n == 32 ? -1 : (1 << n) - 1);//colLim表示列的限制，leftLim表示左斜线的限制，rightLim表示右斜线的限制//1表示已经放了皇后，0表示还没有放皇后return func(limit,0,0,0);}public int func(int limit,int colLim,int leftLim,int rightLim) {if (colLim == limit) {//所有的列上都放了皇后return 1;}int result = 0;//找到可以放皇后的位置（此时1的位置可以放皇后，0的位置不能放皇后）int pos = limit & (~(colLim | leftLim | rightLim));int lastOneIndex = 0;//表示pos的最右侧的1（可以放皇后的位置）while (pos != 0) {lastOneIndex = pos & (~pos + 1);pos -= lastOneIndex;//该位置已经被放皇后，去除result += func(limit,colLim | lastOneIndex,(leftLim | lastOneIndex) << 1,(rightLim | lastOneIndex) >>>1);}return  result;}
}