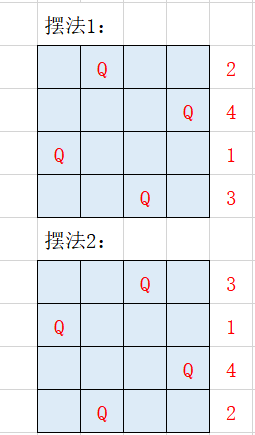
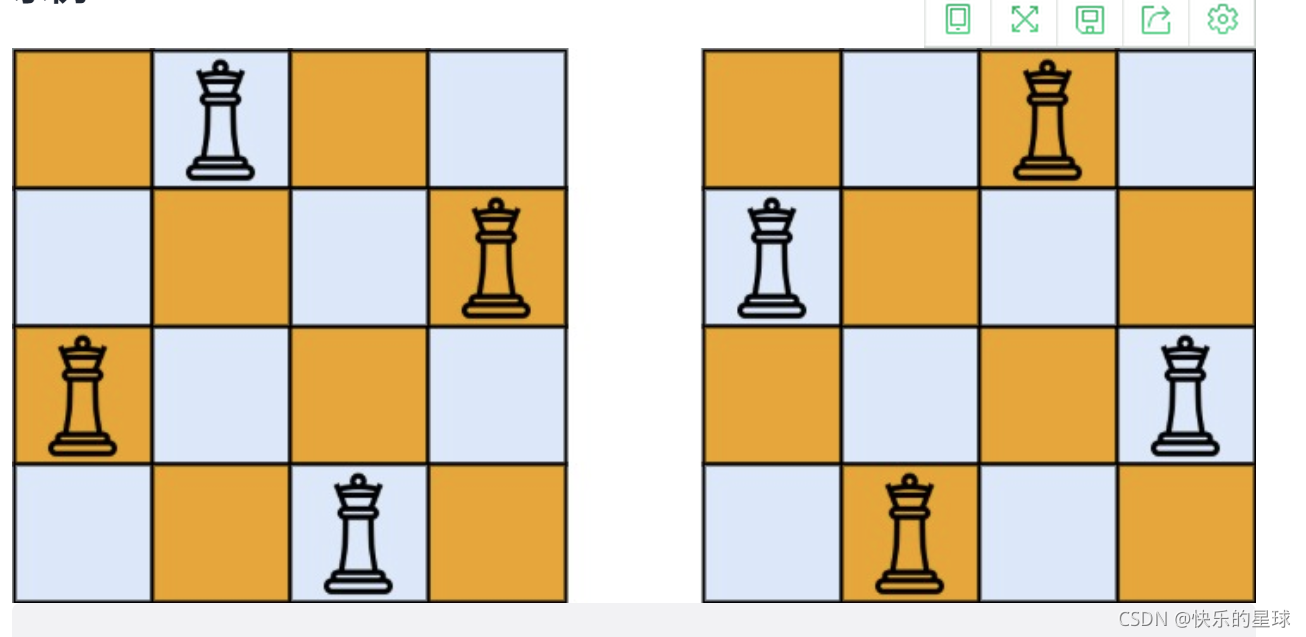
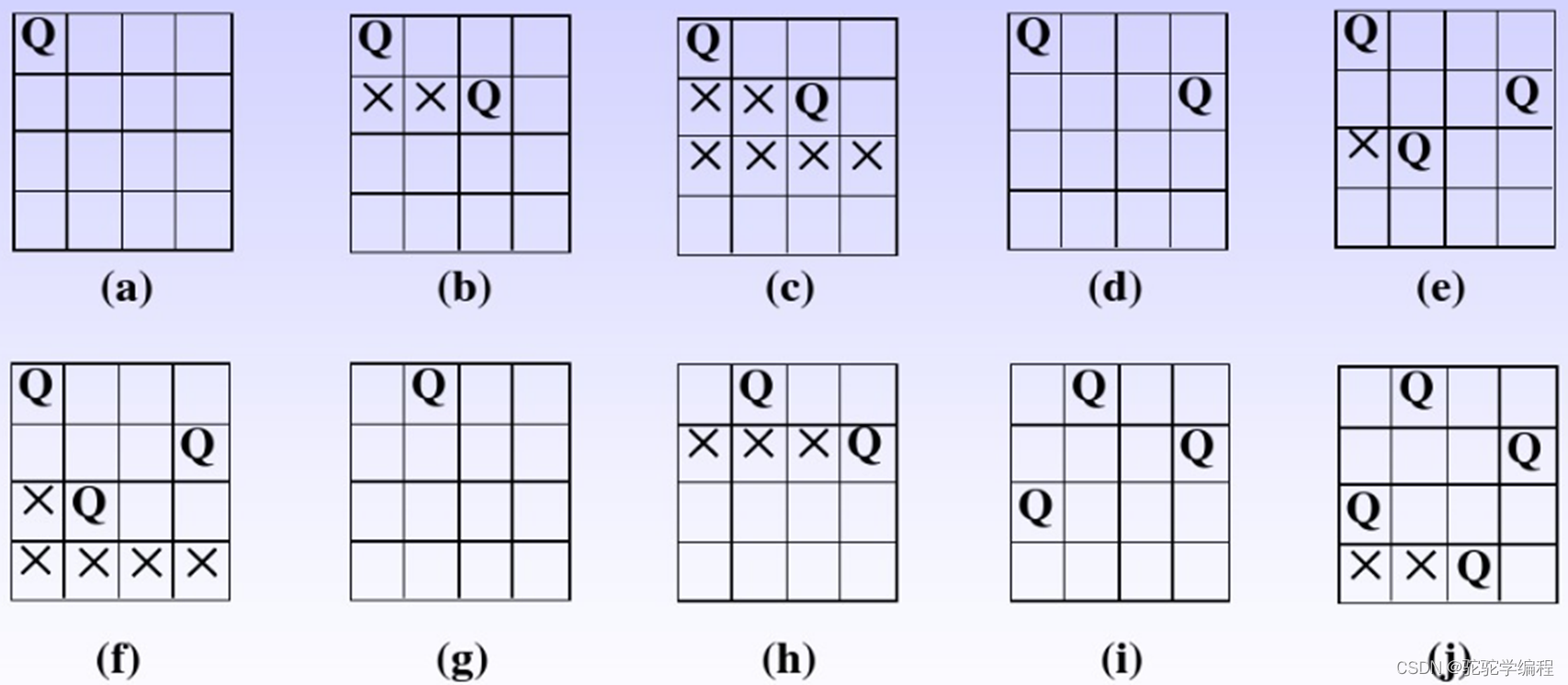
一、N皇后问题的概念

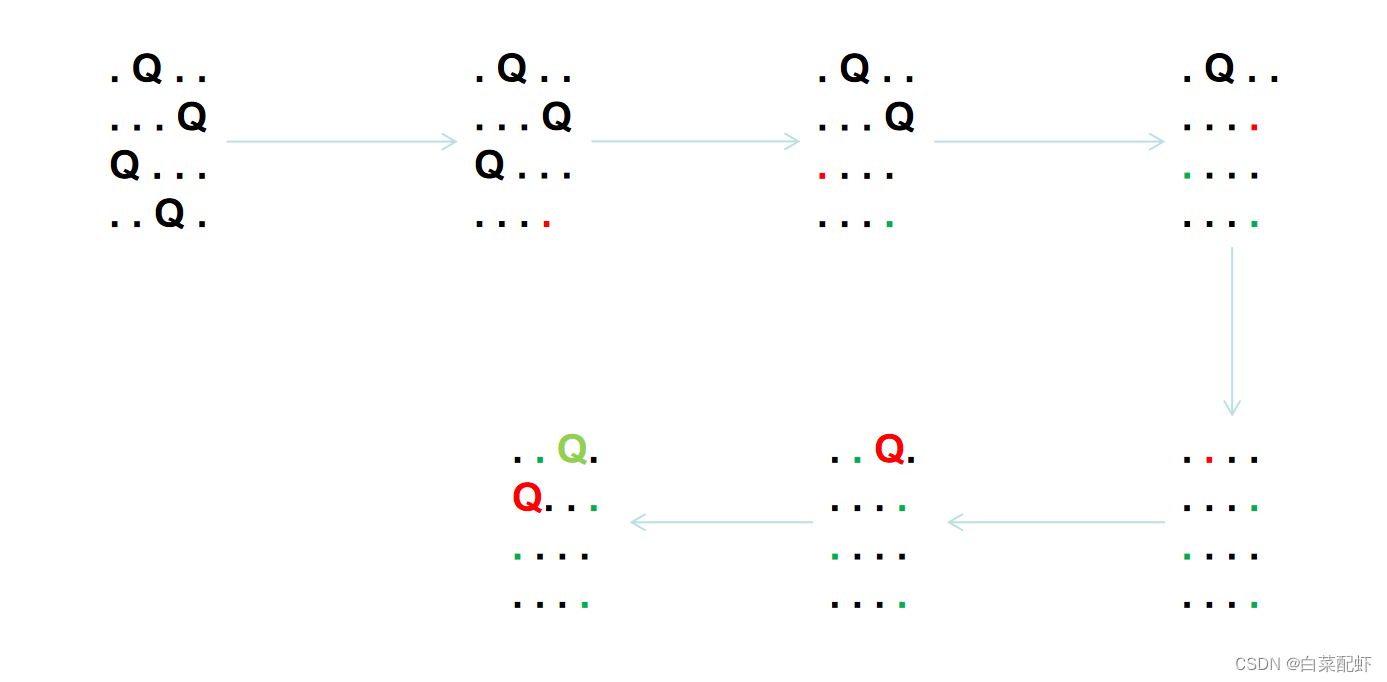
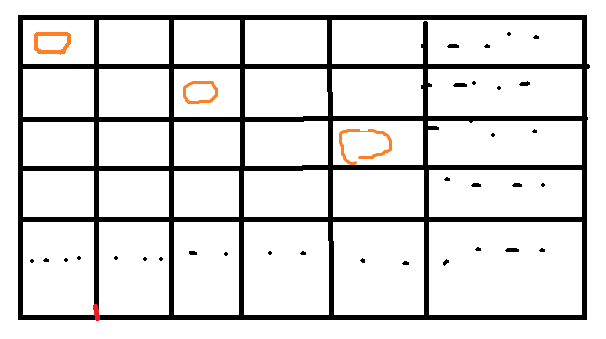
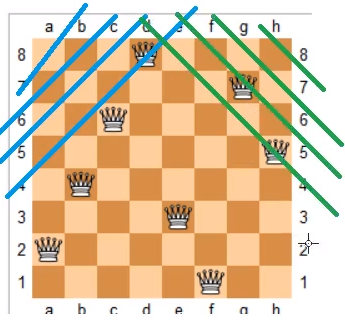
n 皇后问题，研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。 一个皇后可以向水平、垂直以及向斜对角方向移动，如果一个皇后出现在另一个皇后的同一行，同一列或者斜对角，那它就可以被这个皇后攻击。可以通过列举出在棋盘上所有的情况，然后判断每个组合是不是符合的条件。

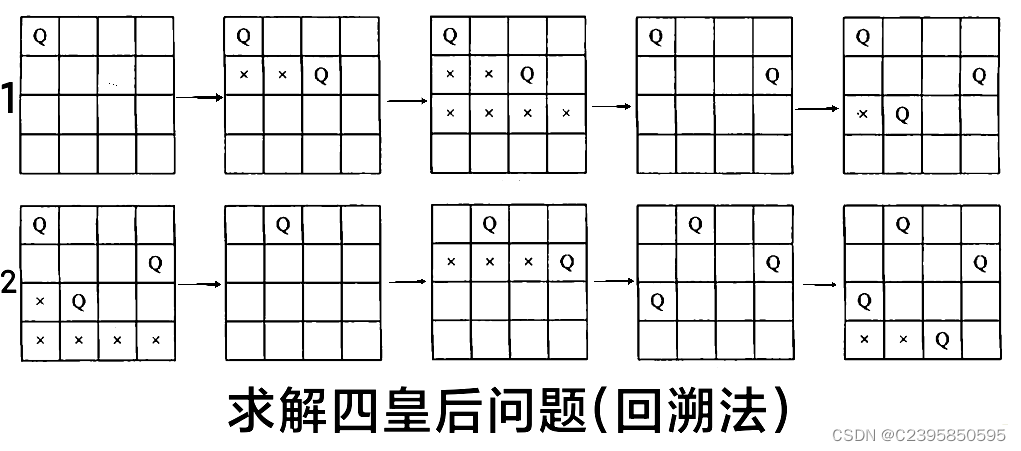
二、代码步骤

1、对皇后位置对错的判断

2、递归实现N皇后位置的排列

3、定义N皇后的指针并初始化

4、代码入口

5、运行结果

---

三、代码功能

1、对皇后位置对错的判断

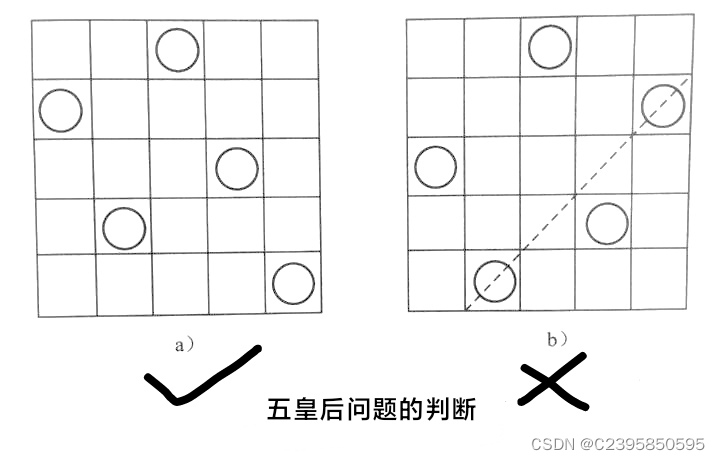
bool place(int* paraSolution, int paraT)
{int j;for(j = 1;j < paraT;j++){if(abs(paraT-j) == abs(paraSolution[paraT]-paraSolution[j]) || paraSolution[paraT] == paraSolution[j])return 0; }return 1;

2、递归实现N皇后位置的排列

void backtracking(int* paraSolution,int paraN,int paraT)
{int i;if(paraT > paraN){for(i = 1; i <= paraN; i++){printf("%d ",paraSolution[i]);//打印出每种符合条件的情况}printf("\r\n");}else{for(i = 1;i <= paraN; i++){paraSolution[paraT] = i;if(place(paraSolution,paraT)){backtracking(paraSolution,paraN,paraT+1);}}}
}

3、定义N皇后的指针并初始化

void nQueen(int paraN)
{int i;int* solution = (int*)malloc((paraN + 1) * sizeof(int));for(i = 0;i <= paraN; i++){solution[i] = 0;}backtracking(solution, paraN ,1);
}

4、代码入口

int main()
{nQueen(5);return 1;
}

5、运行结果

1 3 5 2 4
1 4 2 5 3
2 4 1 3 5
2 5 3 1 4
3 1 4 2 5
3 5 2 4 1
4 1 3 5 2
4 2 5 3 1
5 2 4 1 3
5 3 1 4 2

四、整体代码

#include <stdio.h>
#include <malloc.h>
#include <math.h>bool place(int* paraSolution, int paraT)
{int j;for(j = 1;j < paraT;j++){if(abs(paraT-j) == abs(paraSolution[paraT]-paraSolution[j]) || paraSolution[paraT] == paraSolution[j])return 0; }return 1;
}void backtracking(int* paraSolution,int paraN,int paraT)
{int i;if(paraT > paraN){for(i = 1; i <= paraN; i++){printf("%d ",paraSolution[i]);}printf("\r\n");}else{for(i = 1;i <= paraN; i++){paraSolution[paraT] = i;if(place(paraSolution,paraT)){backtracking(paraSolution,paraN,paraT+1);}}}
}void nQueen(int paraN)
{int i;int* solution = (int*)malloc((paraN + 1) * sizeof(int));for(i = 0;i <= paraN; i++){solution[i] = 0;}backtracking(solution, paraN ,1);
}int main()
{nQueen(5);return 1;
}