✨前言✨

N皇后问题经典的解决方案是暴力递归，其时间复杂度是O(2^n),因此常用来测试计算机的算力。今天我会给大家带来经典方法的详解，也会给大家展示N皇后优化后的大神解法。做一道经典题目，来一场思维旅行。

✨前言✨

💡题目：

🔑传统解法：

代码示例：

大神解法：

💡题目：

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回 n 皇后问题不同的解决方案的数量。

力扣题目链接： N皇后问题

🔑传统解法：

N皇后的传统解法是暴力递归，在我看来暴力递归的精髓就是尝试，N皇后问题要求任意两个皇后都不共行，不共列，不共斜线。因此在一个N*N的棋盘上放N个皇后，因此可以看成由上到下每一行放一个皇后的尝试模型。

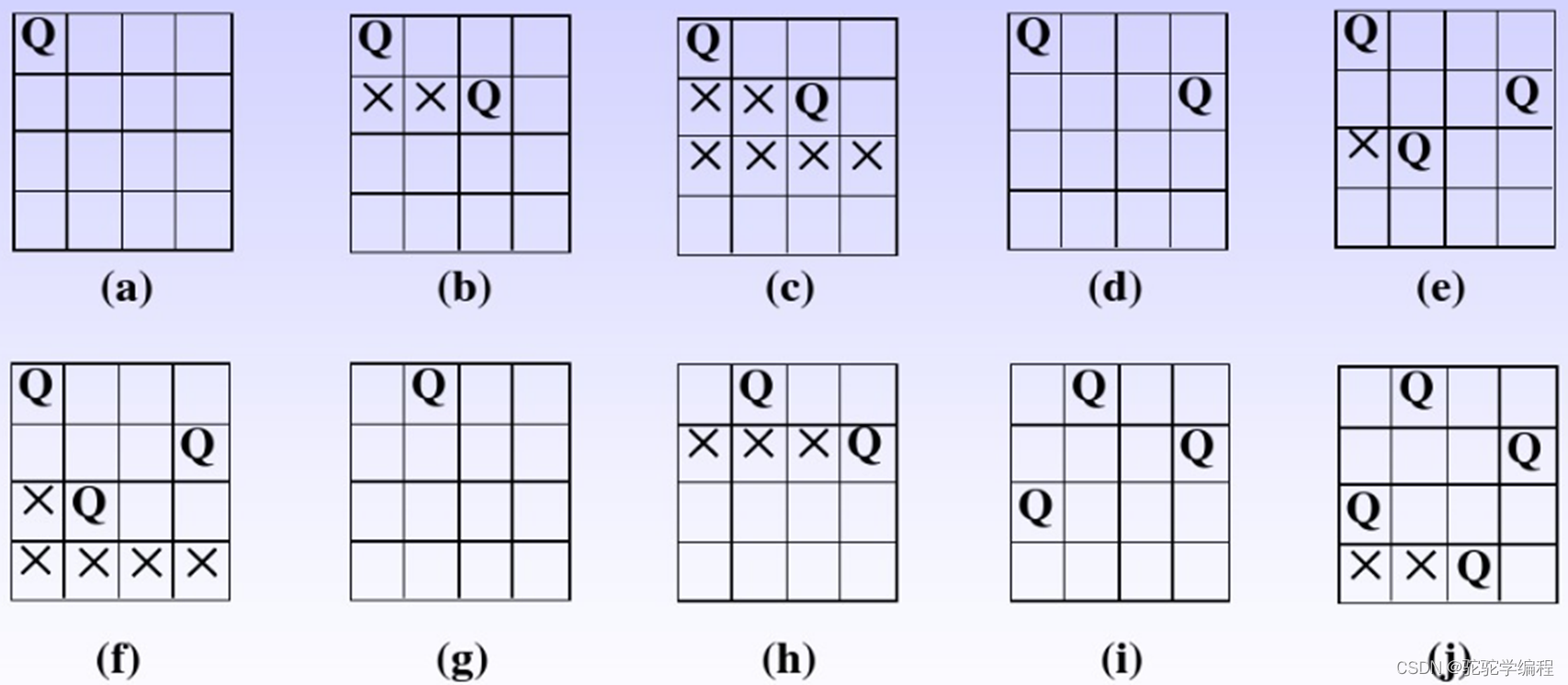
为了更形象的解决这一问题，我们先来看一下图：（来自力扣）

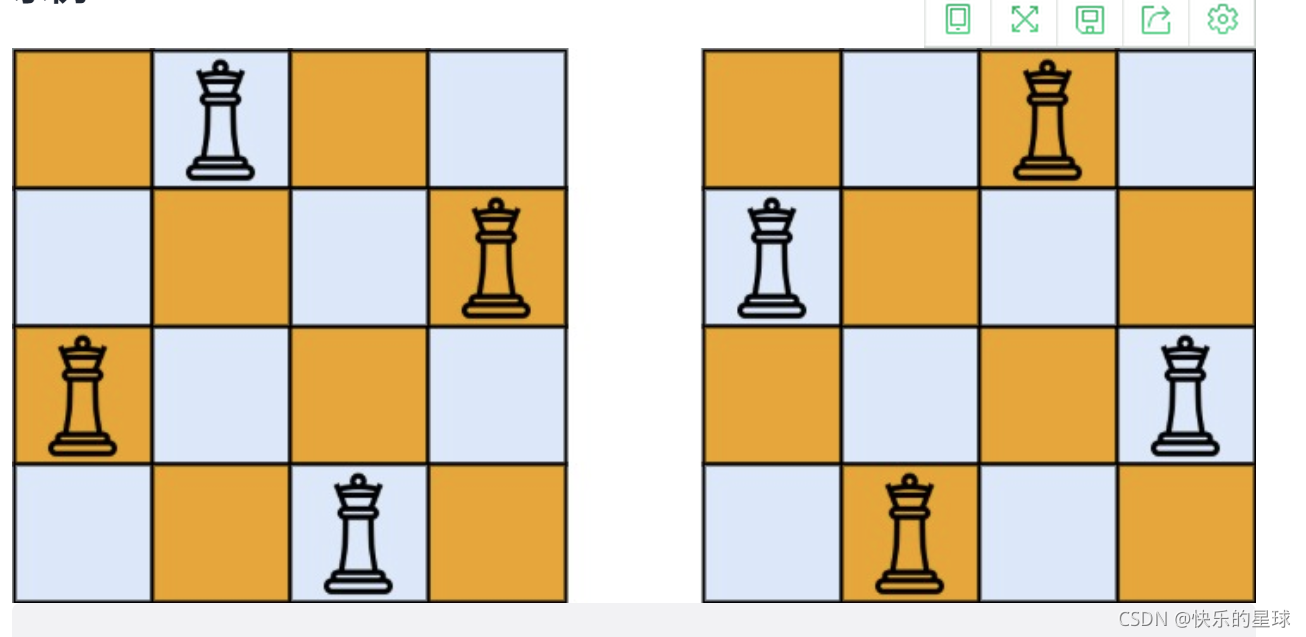
因为我们尝试模型是遍历每一行，每一行尝试放一个皇后，所以所有皇后一定不共行，只需保证在尝试第i个皇后时，第i个皇后与第i-1个皇后不共列，不共斜线，因此我们应该在尝试0-i-1个皇后时，记录下其位置，这样在放第i个皇后时，就可以根据之前所有已经放好的皇后决定第i个皇后应该放哪里。

所以设计的递归函数的参数有三个：

1：变量i表示现在在尝试第i行放第i个皇后

2：变量n表示要放皇后的总数，是一个固定的值，用来标记递归终止条件。

3：数组 result[i] 记录已经放好的皇后在哪一行哪一列，表示第i个皇后所在的列数。

代码示例：

    //暴力递归：N皇后问题的朴素解法//1:当你处理第i行时，我们默认[0...i-1]的皇后都有效摆好了//2:当你摆第i个皇后时，你只需要考虑i个皇后与其它i-1个皇后不共列和不共斜线//三个参数：record[i] 记录下第i个皇后所在的列数//int n表示是几阶皇后问题//int i表示当前处理到了哪一阶public static int process1(int i,int n,int[] record){if(i==n){//当i等于n时，说明N个皇后全部摆放完毕，此时应返回一种解法return 1;}int res=0;//现在轮到摆第i个皇后，//通过遍历第i行的每一列试探每一个位置是否能放皇后for(int j=0;j<n;j++){if(isValid(record,i,j)){//通过isValid函数来判断这个位置是否能放皇后record[i]=j;res+=process1(i+1,n,record);}}return  res;}public static boolean isValid(int[] record,int i,int j){//判断逻辑：如果这个位置与之前的i-1个皇后同列或者共斜线则不能放皇后for(int k=0;k<i;k++){//判断共列以及共斜线if(record[k]==j||(Math.abs(k-i)==Math.abs(record[k]-j))){return false;}}return true;}

大神解法：

我们可以通过位运算来加速算法的常数时间操作。

//n皇后问题大神解法//利用位运算加速，虽然时间复杂度任然是O（2^n）但是其常数时间要低的多//思路：默认每一次递归都能在每一行正确放置一个皇后//这种N皇后的效率比朴素解法要高//limit 范围限制  例如8皇后问题，那么其二进制序列的后8位全是1，左边其他位全是无效位//colLim 列限制   二进制序列中为0的地方标志这一列还没有放过皇后，如果是1表示这一列已经放了皇后//leftDiaLim左斜线限制    表示由于放了0-i-1个皇后，而导致在放第i个皇后时，由于左斜线限制，//                      使得第i行不能放皇后的列全标记为1//rightDiaLim 右斜线限制  同理public static int quickNQueue(int N){if(N<1||N>32){//因为int最多32个字节，超过32皇后问题要把in改成longreturn 0;}int limit=N==32?-1:(1<<N)-1;//定义出limit n皇后问题则limit的后n为全是1其他为全为0return process2(limit,0,0,0);}//因为我们要用位运算来加速，因此递归函数所有整型参数都应该看成0-1构成的序列public static int process2(int limit,int colLim,int leftDiaLim,int rightDiaLim){if(colLim==limit){return 1;}int res=0;int pos=limit&(~(colLim|leftDiaLim|rightDiaLim));//在范围内可以放皇后的位置全标记位1int mostRightOne=0;while(pos!=0){//摆第i个皇后逻辑//在pos中二进制序列为1的位置能放皇后，我们每一次取最右侧的1位置放皇后mostRightOne=pos&(~pos+1);//拿出最右侧的一个1其它位全变成0，并在这个位置放皇后pos-=mostRightOne;//pos最右侧为1的位置改成0，说明这个位置已经放了皇后//更新参数直接递归摆剩下所有的皇后res+=process2(limit,colLim|mostRightOne,//这一列已经放了皇后，标记为1(leftDiaLim|rightDiaLim)<<1,//更新这个皇后的左斜线限制(rightDiaLim|mostRightOne)>>>1//更新这个皇后的右斜线限制);}return res;}