3.2 回溯法—N皇后问题

article/2025/10/6 3:34:52

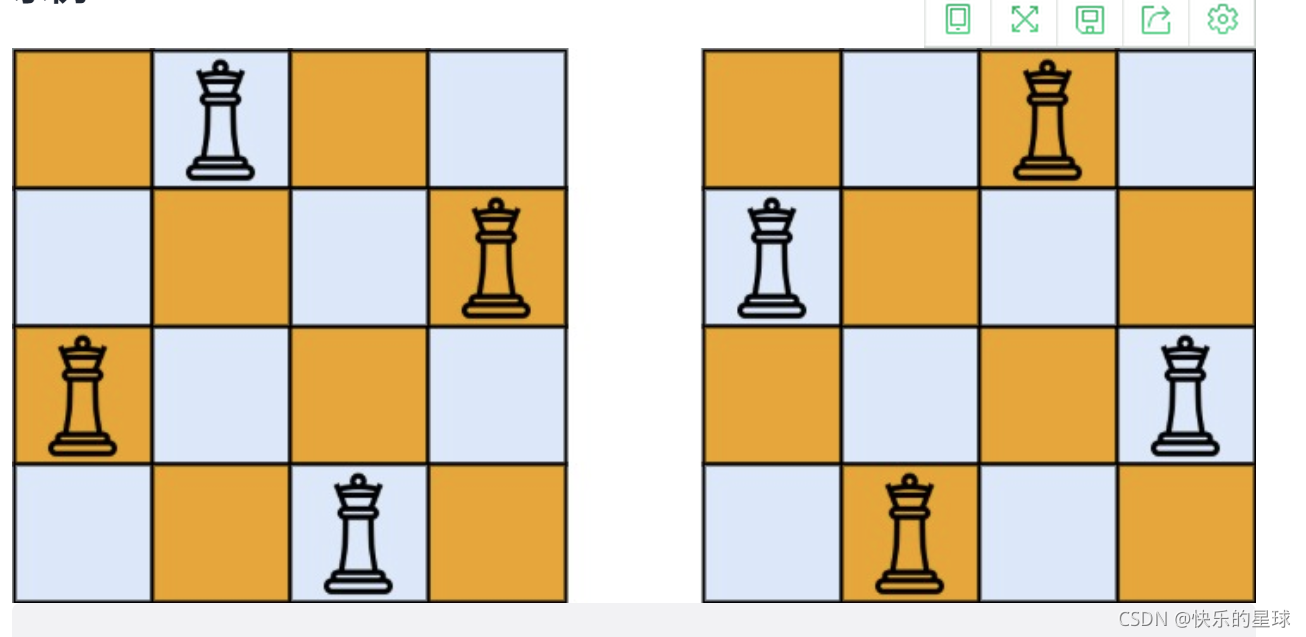
1. 问题描述

在 $n\times n$ 的棋盘上摆放 $n$ 个皇后，使任意两个皇后都不能处于同一行、同一列或同一斜线上

2. 问题分析

在这里插入图片描述
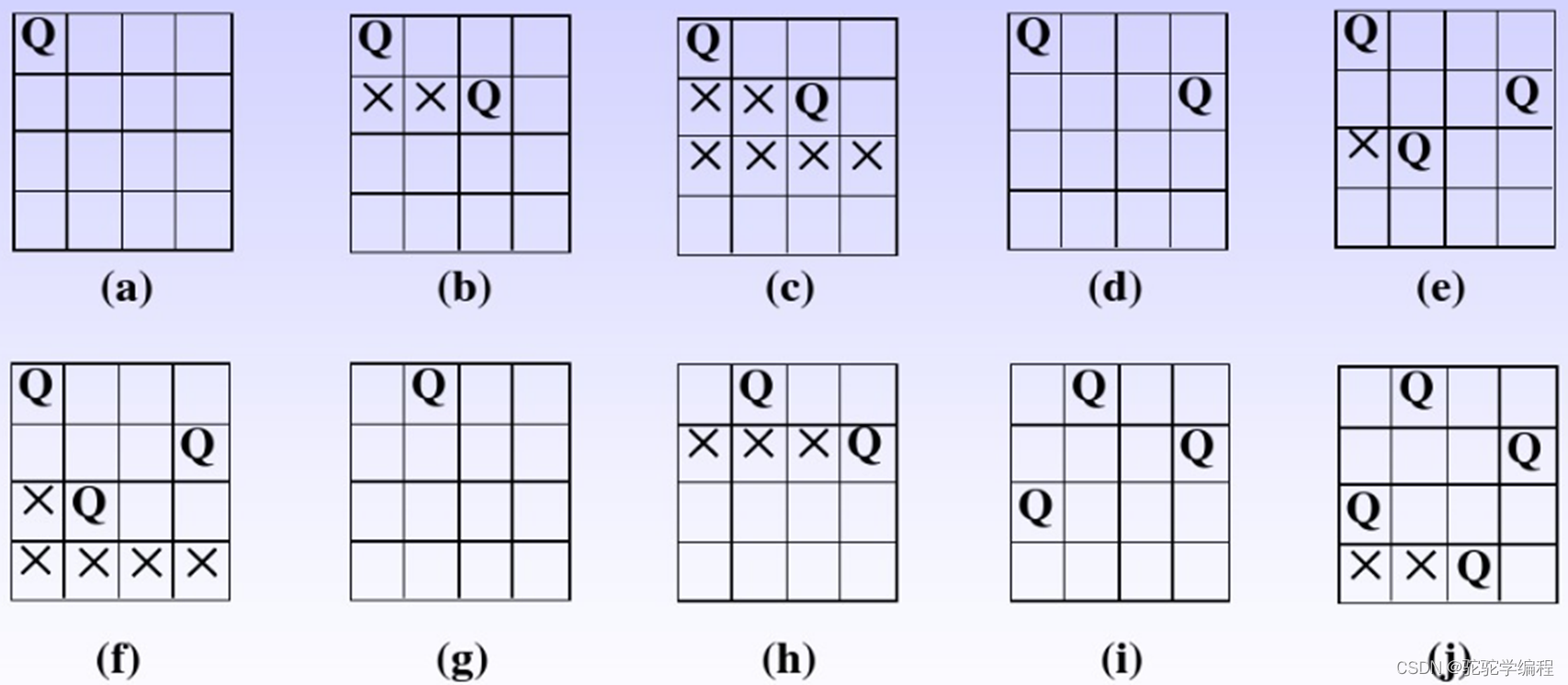
下以求解4皇后问题为例，分析4皇后问题的排列树以及回溯过程：

搜索及回溯过程：

解空间树：
在这里插入图片描述

3. 算法设计

1. 算法思想

①用数组x[]存放皇后的位置，x[k]表示第k个皇后放置的位置
②先在第一行放置第1个皇后，然后依2、3、…、n的次序放置其他皇后，当第n个皇后放置好后产生一个可行解（为得到所有解，还需要继续试探第n个皇后的下一个位置）
③试探每个皇后的位置都是从第1列开始的
④当第k个皇后试探了所有列都不能放置时，则回溯到第k-1个皇后，试探第k-1个皇后的下一个位置：如果第k-1个皇后的列号x[k-1]<n，则将其移到下一列，继续试探；否则，再回溯到第k-2个皇后，依次类推
⑤放置第k个皇后应与前面已经放置的k-1个皇后不发生冲突
⑥若第1个皇后的所有位置回溯完毕，则算法结束

2. 代码实现

#include<stdio.h>
#include<math.h>
#include<string>
//考察皇后k放置在x[k]列是否发生冲突
int Place(int k, int x[]) {											for (int i = 1; i < k; i++)/* x[k] == x[i]：是否在同列Math.abs(k - i) == Math.abs(x[k] - x[i])：是否在同一斜线*/if (x[k] == x[i] || fabs(k - i) == fabs(x[k] - x[i]))return 1;										//冲突则返回1return 0;
}
/*求解n皇后问题
*/
//非递归算法
void Queens(int n, int x[]) {							int i = 1;												//i表示当前行，也表示放置第i个皇后x[i] = 0;												//x[i]是当前列，每个新考虑的皇后初始位置置为0列while (i >= 1) {										//尚未回溯到头，循环x[i]++;												//原位置后移动一列while (x[i] <= n && Place(i, x) == 1)				//发生冲突，试探下一个位置(i, x[i])x[i]++;if (x[i] <= n) {									//为第i个皇后找到了一个合适位置(i, x[i])if (i == n) {									//若放置了所有皇后，输出一个解for (int k = 1; k <= n; k++)printf("%d ", x[k]);printf("\n");}else {											//若皇后没有放置完i++;										//转向下一行，即开始下一个新皇后的放置x[i] = 0;									//每个新考虑的皇后初始位置置为0列}}else i--;											//若第i个皇后找不到合适的位置，则回溯到上一个皇后}
}//递归算法
void Queens(int i, int x[]， int n){
if(i > n){for (int k = 1; k <= n; k++)							//n个皇后都放置好，输出printf("%d ", x[k]);printf("\n");
}elsefor(int j = 1; j <= n; j++){							//每层均有n种放法x[i] = j;											//放置皇后t在第i列即x[t]if(Place(i, x) == 0)								//不冲突，考察皇后t放置在x[t]列是否发生冲突Queens(i+1, x, n);								//继续递归放置下一个皇后}		
}void main() {int n;printf("请输入皇后个数：");scanf_s("%d", &n);int *x = (int *)malloc(sizeof(int)*(n+1));//非递归调用Queens(n, x);//递归调用//Queens(1, x, n);
}