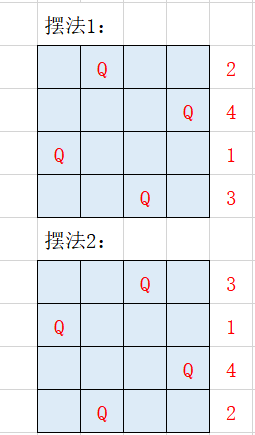
非常经典的一道题:
N皇后问题:
国际象棋中皇后的势力范围覆盖其所在的行、列以及两条对角线,现在考察如下问题:如何在n x n的棋盘上放置n个皇后,使得她们彼此互不攻击 。
免去麻烦我们这里假定n不是很大。。

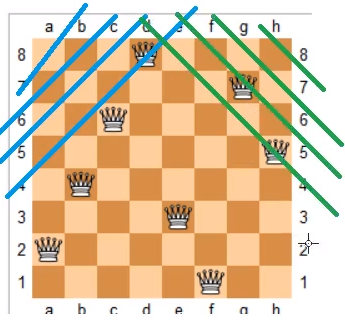
(图片来自百度百科(这是8皇后问题的一种解法))
某leetcode大犇曾说过:“这个问题和解数独题目有一个很大的共同点,那就是:我都不会。”
好了下面开始分析:(废话警告)
初步判断这问题的特点有:
1.有个场地来放置单位。
2.各个单位之间有制约。
3.没有特殊的数学方法,得把某一个摆法摆出来才能判断是否可行。
于是萌新一般都会这么想:对于1,:我搞个二维数组来存。对于2:我搞个判定函数来一个一个判定。对于3:我暴力枚举。
那么算法框架大概就是:我对二维数组的所有情况进行枚举,然后对每种情况进行判定
over ,输个数字n,按下回车,双手离开键盘,等了老半天发现命令提示符只有个光标在跳动 |
如果是在做网题,说不定就判定是超时或者内存溢出,过不了。
然后就开始思考怎么优化:
对于1,我可以缩减吗····,改成一维数组,,,似乎徒增麻烦。
对于2,我可以有更巧妙的判断方法吗?·············有个鬼,还不得把每个棋子的每一行每一列每两个斜线都瞅一下。
对于3,我一定要把所有情况都举出来嘛?···(于是脑子里面开始摆起了棋子,模拟算法过程)
然后就会发现 比如第一行前两个格子一开始就摆了两个相邻的棋子,诶这不明摆着皇后互怼了吗!后面还继续枚举就太傻了吧···
这种傻事情做了不是白白增加耗时吗!
所以就思考如何在这种“傻情况”出现的时候就pass掉后面所有情况。。。
于是脑子陷入了一团乱麻。。。
打住!
咱们换个思考方式,既然直接想有点困难,不如我们想办法先做点处理,让这些玩意儿便于我们把弄。
再回头想想规则,皇后可以吃掉所处的一行一列以及斜线上的棋子,那也就是说,每一行都最多只能有一个棋子,每一列都最多只能有一个棋子,
那我们不妨把每一行看成一组!
那么这一组就只有n个可能性(一行n个位置 每一次只有一个位置被占用)
也就是单个一行有n种可能性
因为有n行
哈哈那么就瞬间只需要讨论n*n种可能性了!
还记得我们之前的思考吗?:
对于3,我一定要把所有情况都举出来嘛?···(于是脑子里面开始摆起了棋子,模拟算法过程)然后就会发现 比如第一行前两个格子一开始就摆了两个相邻的棋子,诶这不明摆着皇后互怼了吗!后面还继续枚举就太傻了吧···这种傻事情做了不是白白增加耗时吗!所以就思考如何在这种“傻情况”出现的时候就pass掉后面所有情况。。。像这种情况:
(我的天这皇后画的...)
显然下面3,4,5····行都不用枚举了,直接pass掉
于是我们思路慢慢清晰了起来:
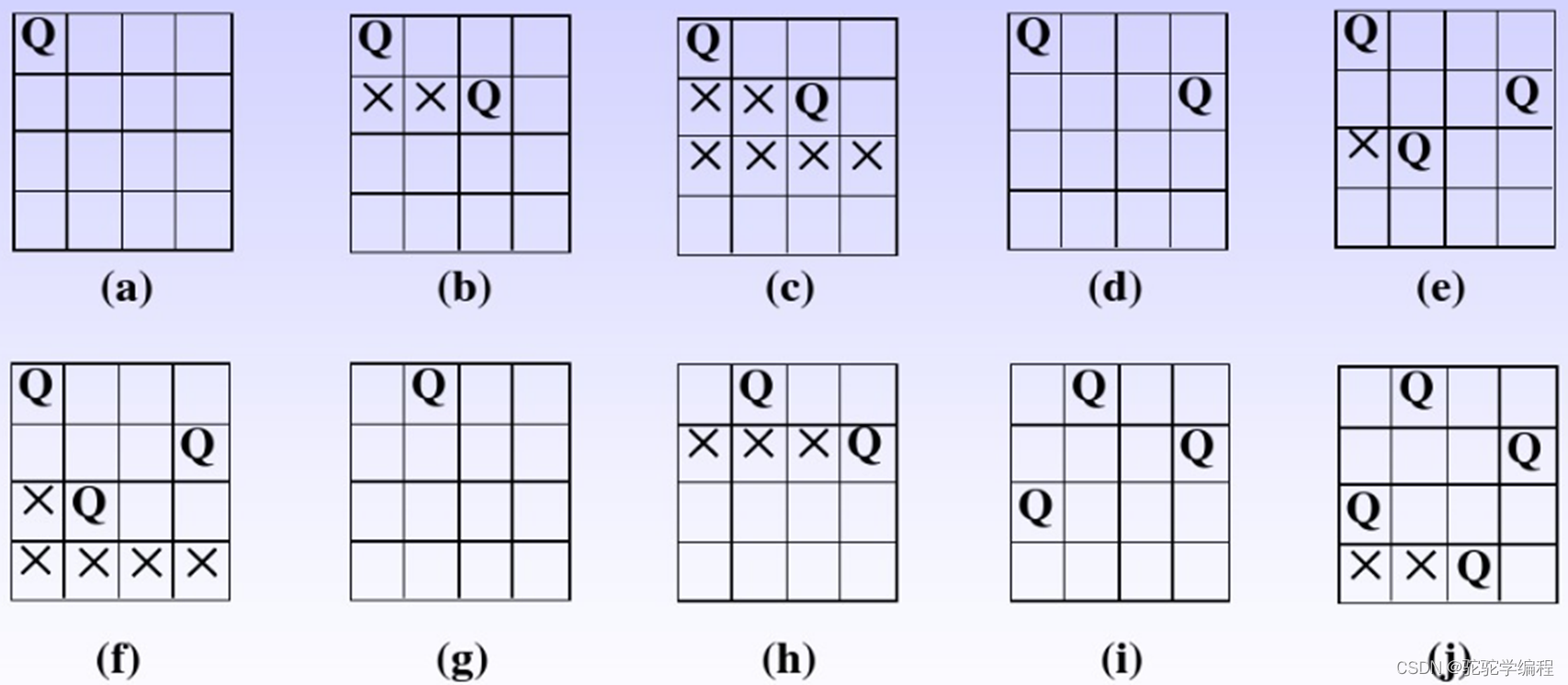
我们从第一行开始枚举,第一行第一格:

然后枚举第二行,也从第一格开始:

判定一下,哇,不行,咋办呢?这情况下面所有行都没有枚举的必要了,但是本行还是可以继续的。。。于是我们开始枚举第二行第二个情况:

不行(斜线上互吃)。
继续第二行下一个情况:

行嘞!
那么我们就可以开第三行了:

不行(一列上吃)。

不行(斜线上吃)

不行。

还不行
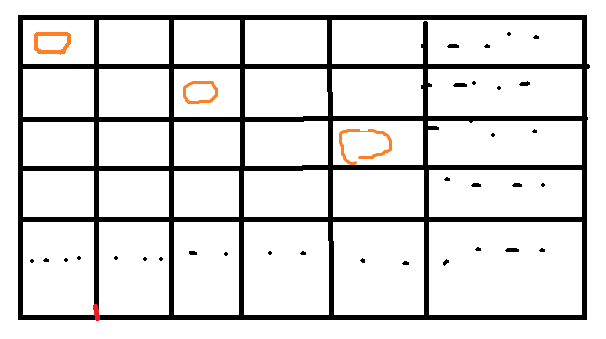
行嘞!
··················
好了,算法思路大概就出来了。
我们就这样干下去,直到最后一行可行,那么我们就获得了一个可行解了,
然后我们想继续获得其他解,那么继续枚举下去,但是要退一步:
先从倒数第一行开始,我们枚举下一个,有解则输出,无解则继续。
倒数第一行结束了,咋办?
别忘了倒数第二行的情况还不一定枚举完了呢。
于是退到倒数第二行,继续如上操作。
··················
干说着没用,撸代码:
#include<iostream>using namespace std;
int main()
{return 0;
}先准备好需要用的存储(这里用64个绰绰有余)
ans是用来存每一次的解 ans[1]表示第一行的那个元素的所在列的位置
#include<iostream>using namespace std;
bool colMark[64] = { 0 };//元素所在列 如果有了元素在第k列 那么colMark[k]就标记上true
bool naMark[64] = { 0 };//捺,撇···顾名思义,表示元素所在的两个斜线o.o 原理同上
bool pieMark[64] = { 0 };
int total = 0; //解的总个数
int N = 0;
int ans[64] = { 0 };
int main()
{return 0;
}然后下面先写一个显示函数:
void showOneSolution()//用来显示一个解
{total++;for (int i = 1; i<=N; ++i){cout << ans[i] << " ";}cout << endl;
}下面是核心:
void Dfs(int i) //可以百度学习 深度优先搜索
{if (i > N) //判断是否已经枚举完了N行 {showOneSolution(); //枚举完了就输出(此刻我们处于N+1行)return; //返回到第N行}for (int j = 1; j <= N; ++j) //这里的j表示 本行的第j列{if ((!colMark[j])&&(!naMark[j-i+N])&&(!pieMark[i+j])) //这里的"j-i+N" "i+j"建议自己体会{ //判断这个格子所在的两个斜线和所在列是否为空colMark[j] = true;naMark[j - i + N] = true;pieMark[i + j] = true;ans[i] = j;Dfs(i + 1);colMark[j] = false; //这个格子枚举完了要进入本行第j+1个格子(或者结束本行) 走之前别忘了恢复标记naMark[j - i + N] = false;pieMark[i + j] = false;}}
}最后组装起来:(当然啦,还是建议自己撸代码,你会发现很多意想不到的问题~解决问题的同时也是进步)
#include<iostream>using namespace std;
bool colMark[64] = { 0 };
bool naMark[64] = { 0 };
bool pieMark[64] = { 0 };
int total = 0;
int N = 0;
int ans[64] = { 0 };
void showOneSolution()//用来显示一个解
{total++;for (int i = 1; i<=N; ++i){cout << ans[i] << " ";}cout << endl;
}
void Dfs(int i)
{if (i > N) //判断是否已经枚举完了N行{showOneSolution(); //枚举完了就输出(此刻我们处于N+1行)return; //返回到第N行}for (int j = 1; j <= N; ++j) //这里的j表示 本行的第j列{if ((!colMark[j]) && (!naMark[j - i + N]) && (!pieMark[i + j])){ //判断这个格子所在的两个斜线和所在列是否为空colMark[j] = true;naMark[j - i + N] = true;pieMark[i + j] = true;ans[i] = j;Dfs(i + 1);colMark[j] = false; // 走之前别忘了恢复标记naMark[j - i + N] = false;pieMark[i + j] = false;}}
}
int main()
{cin >> N;Dfs(1);cout << total;system("pause");return 0;
}总结:
思路混乱不妨换个角度理一理。
在纸上面画一画算法过程会有不少帮助。
代码少出错还是得多撸。
想什么呢?!撸代码!