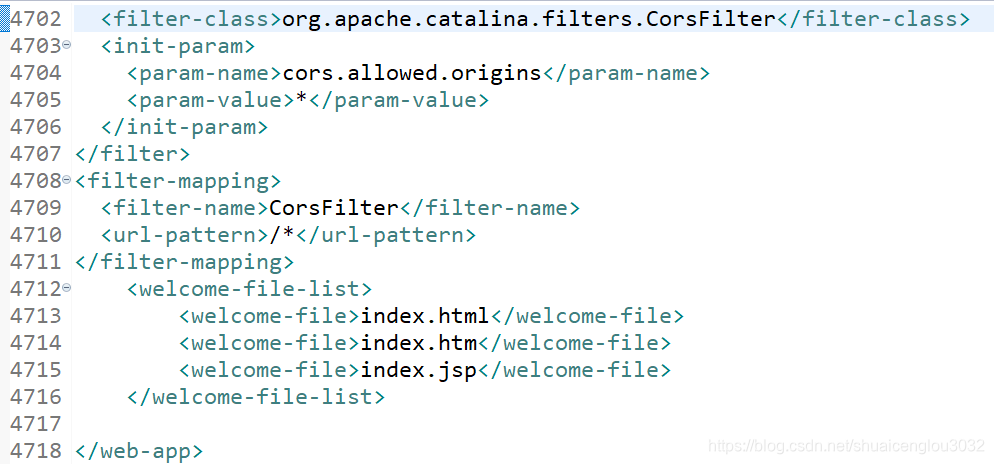
八皇后问题是dfs的经典问题,目前遇到过的类型大致有这么几种:
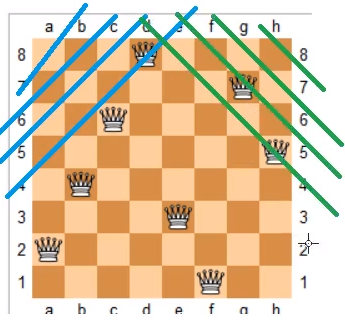
1.经典n皇后问题
题目描述
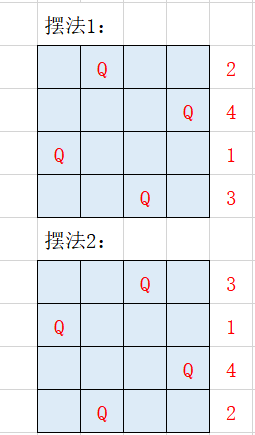
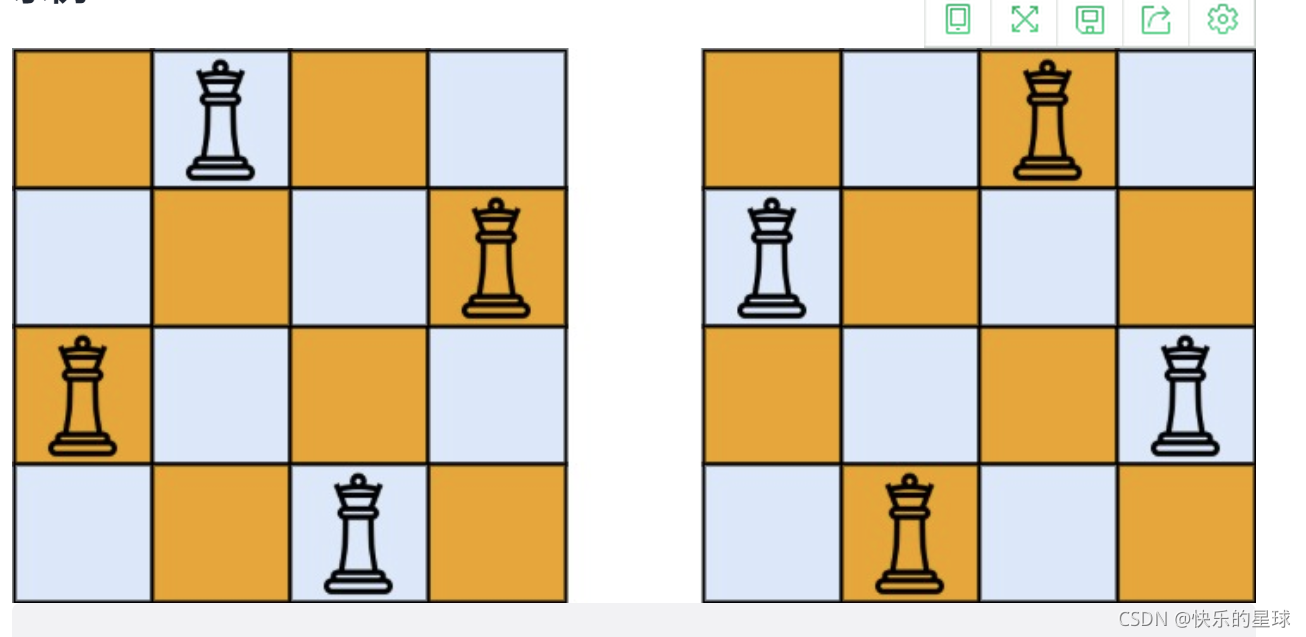
n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
输入格式
现在给定整数 n,请你输出所有的满足条件的棋子摆法。
输出格式
每个解决方案占 n 行,每行输出一个长度为 n 的字符串,用来表示完整的棋盘状态。
其中 . 表示某一个位置的方格状态为空,Q 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
输入样例
4
输出样例
.Q..
...Q
Q...
..Q...Q.
Q...
...Q
.Q..分析
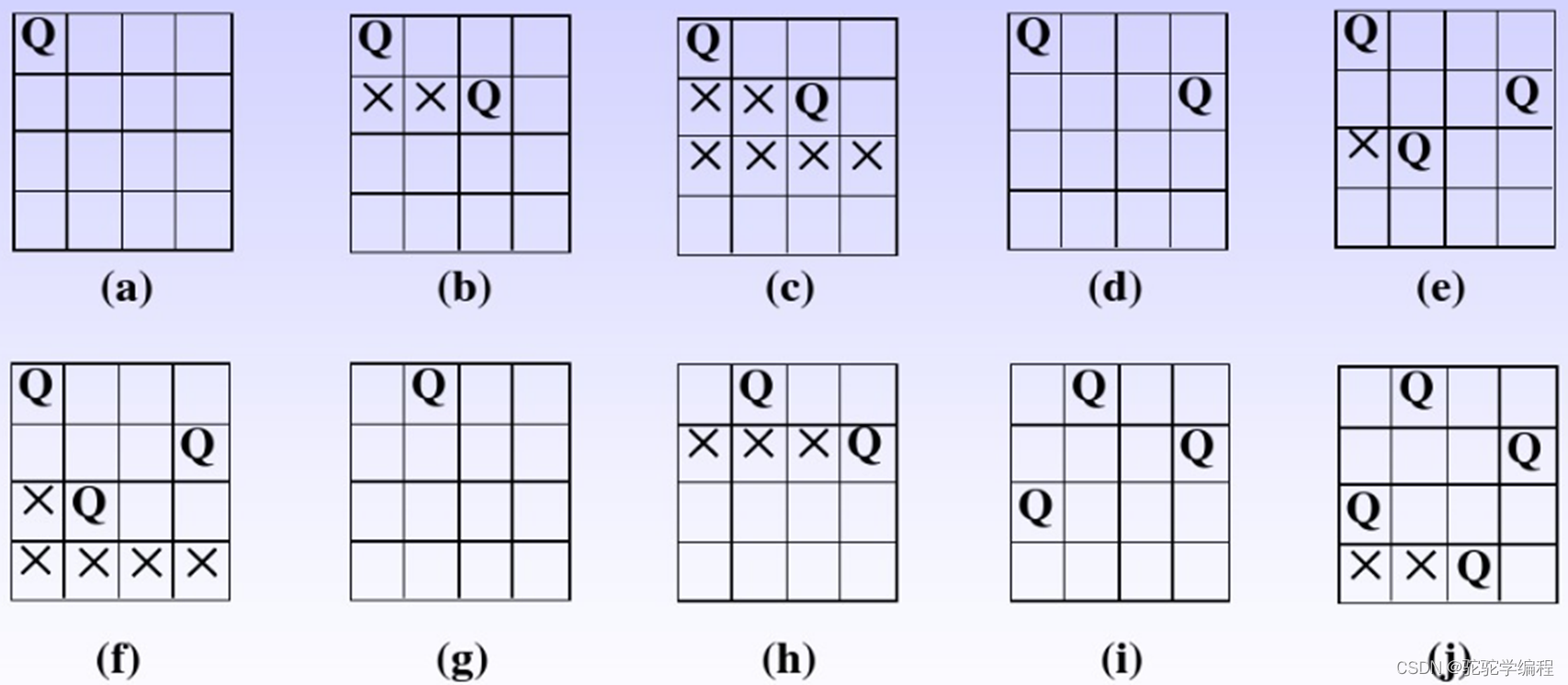
设置三个数组 col[N],dg[N],udg[N]; 判断每一列,每一个对角线,反对角线上是否放了皇后。
C++ 代码
#include<bits/stdc++.h>
using namespace std;const int N = 20;int n;
char path[N][N];
bool col[N],dg[N],udg[N];
void dfs(int x)
{if(x == n){for(int i=0;i<n;i++) {printf("%s\n",path[i]);}printf("\n");return ; }for(int i=0;i<n;i++){if(!col[i] && !dg[x+i] && !udg[n-x+i]){path[x][i]='Q';col[i]=dg[x+i]=udg[n-x+i] = true;dfs(x+1);path[x][i]='.';col[i]=dg[x+i]=udg[n-x+i] = false;}}
}
int main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++){path[i][j]='.';}}dfs(0);return 0;}
2.八皇后
题目描述
会下国际象棋的人都很清楚:皇后可以在横、竖、斜线上不限步数地吃掉其他棋子。
如何将 8 个皇后放在棋盘上(有 8×8 个方格),使它们谁也不能被吃掉!
这就是著名的八皇后问题。
对于某个满足要求的 8 皇后的摆放方法,定义一个皇后串 a 与之对应,即 a=b1b2…b8,其中 bi 为相应摆法中第 i 行皇后所处的列数。
已经知道 8 皇后问题一共有 92 组解(即 92 个不同的皇后串)。
给出一个数 b,要求输出第 b 个串。
串的比较是这样的:皇后串 x 置于皇后串 y 之前,当且仅当将 x 视为整数时比 y 小。
输入格式
第一行包含整数 n,表示共有 n 组测试数据。
每组测试数据占 1 行,包括一个正整数 b。
输出格式
输出有 n 行,每行输出对应一个输入。
输出应是一个正整数,是对应于 b 的皇后串。
输入样例
2
1
92
输出样例
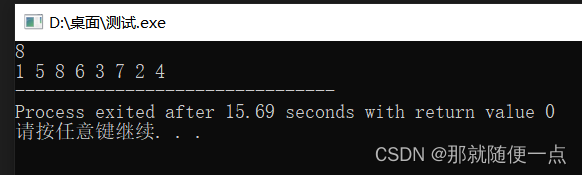
15863724
84136275
分析
由题意可得,一共存在92中合法性情况,所以只需要将这92次都先存储在结果数组中,之后直接输出即可。
C++ 代码
#include<bits/stdc++.h>
using namespace std;
const int N =20;
bool col[N],dg[N],udg[N];
int n,x;
vector<string> path;
void dfs(int u,string s)
{if(u==8){path.push_back(s);return ;}for(int i=0;i<8;i++){if(!col[i] && !dg[u+i] && !udg[u-i+8]) {col[i]=dg[u+i]=udg[u-i+8]=1;s+=(i+'1');dfs(u+1,s);s.pop_back();col[i]=dg[u+i]=udg[u-i+8]=0;}}
}
int main()
{dfs(0,"");sort(path.begin(),path.end());cin>>n;while(n--){cin>>x;cout<<path[x-1]<<endl;}return 0;
}
3.八皇后*改
题目描述
规则同8皇后问题,但是棋盘上每格都有一个数字,要求八皇后所在格子数字之和最大。
输入格式
一个8*8的棋盘。
数据规模和约定
棋盘上的数字范围0~99
输出格式
所能得到的最大数字和
输入样例
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
48 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64
输出样例
260
分析
由经典八皇后问题可得,一共存在92中合法性情况,所以只需要将这92次的结果取最大值就可以了。
C++ 代码
#include<bits/stdc++.h>
using namespace std;
int ans,g[10][10];
bool col[10],dg[20],udg[20];
void dfs(int u,vector<int> v)
{if(u==8){int res=0;for(int i=0;i<8;i++){res+=g[i][v[i]];}ans=max(res,ans);}for(int i=0;i<8;i++){if(!col[i] && !dg[u+i] && !udg[u-i+8]){col[i]=dg[u+i]=udg[u-i+8]=1;v.push_back(i);dfs(u+1,v);v.pop_back();col[i]=dg[u+i]=udg[u-i+8]=0;}}
}
int main()
{for(int i=0;i<8;i++){for(int j=0;j<8;j++)cin>>g[i][j];}vector<int> v;dfs(0,v);cout<<ans;return 0;
}
4.2n皇后问题
题目描述
给定一个n*n的棋盘,棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后和n个白皇后,使任意的两个黑皇后都不在同一行、同一列或同一条对角线上,任意的两个白皇后都不在同一行、同一列或同一条对角线上。
问总共有多少种放法?
n小于等于8。
说明:同一条对角线是指包括两条主对角线的所有对角线,n=5时的棋盘从左上往右下有9条对角线,从右上往左下也有9条对角线。
比如,棋盘为:
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
表示一个4*4的棋盘,所有位置都可放皇后。
则可知有2种放法。
输入格式
输入的第一行为一个整数n,表示棋盘的大小。
接下来n行,每行n个0或1的整数,如果一个整数为1,表示对应的位置可以放皇后,如果一个整数为0,表示对应的位置不可以放皇后。
输出格式
输出一个整数,表示总共有多少种放法。
输入样例
4
1 0 1 1
1 1 1 1
1 1 1 1
1 1 1 1
输出样例
0
分析
本题与八皇后*改题目类似,不过要进行两次皇后摆放,一次摆黑色皇后(染色为2),一次摆白色皇后(染色为3),最后判断是否所有的n个黑皇后和n个白皇后都摆在了正确的位置上,若正确,就算作一次合法样例,ans++。
C++ 代码
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
bool colb[N],dgb[N*2],udgb[N*2],colw[N],dgw[N*2],udgw[N*2];
int n,g[N][N],cntb,cntw,ans;
void dfsw(int u,int color) //后给白色皇后摆放染色
{if(u==n) //摆完了判断是否为合法方案{if(cntb==n && cntw==n) ans++;return ;}for(int i=0;i<n;i++){if(!colw[i] && !dgw[u+i] && !udgw[u-i+n] && g[u][i]==1){colw[i]=dgw[u+i]=udgw[u-i+n]=1;int t=g[u][i];g[u][i]=3;cntw++;dfsw(u+1,3);cntw--;g[u][i]=t;colw[i]=dgw[u+i]=udgw[u-i+n]=0;}}}
void dfsb(int u,int color) //先给黑色皇后摆放染色
{if(u==n) //摆完了黑色就摆白色{dfsw(0,3);return ;}for(int i=0;i<n;i++){if(!colb[i] && !dgb[u+i] && !udgb[u-i+n] && g[u][i]==1){colb[i]=dgb[u+i]=udgb[u-i+n]=1;int t=g[u][i];g[u][i]=2;cntb++;dfsb(u+1,2);cntb--;g[u][i]=t;colb[i]=dgb[u+i]=udgb[u-i+n]=0;}}
}
int main()
{cin>>n;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>g[i][j];}}dfsb(0,2);cout<<ans;return 0;
}
5.王、后传说
题目描述
地球人都知道,在国际象棋中,后如同太阳,光芒四射,威风八面,它能控制横、竖、斜线位置。
看过清宫戏的中国人都知道,后宫乃步步惊心的险恶之地。各皇后都有自己的势力范围,但也总能找到相安无事的办法。
所有中国人都知道,皇权神圣,伴君如伴虎,触龙颜者死…
现在有一个n*n的皇宫,国王占据他所在位置及周围的共9个格子,这些格子皇后不能使用(如果国王位于王宫的边缘,占用的格子可能不到9个)。当然,皇后也不会攻击国王。
现在知道了皇宫的规模n,国王的位置(x,y)(国王位于第x行第y列,行和列号从1开始),请问,有多少种方案放置n个皇后,使她们不能互相攻击(同一横线、竖线、斜线上只能有一个皇后)。
输入格式
输入仅一行,包含三个整数,表示皇宫的规模n(n<=12)及国王的位置x和y坐标。
输出格式
一个整数,表示放置n个皇后的方案数
输入样例
8 2 2
输出样例
10
分析
本题属于棋盘有限制的皇后问题,国王所在的九宫格可以提前标记为1,不能防置,其他位置可以随便摆放皇后,如果摆到最后一行发现正好摆好了n个皇后,则属于一种合法情况。
C++ 代码
#include<bits/stdc++.h>
using namespace std;
const int N=30;
int n,a,b,cnt,ans;
bool col[N],dg[N],udg[N],st[N][N];
void dfs(int u)
{if(u==n) //摆到最后刚好n个皇后{if(cnt==n) ans++;return ;}for(int i=0;i<n;i++){if(!col[i] && !st[u][i] && !dg[u+i] && !udg[u-i+n]) //此地可以摆皇后{col[i]=dg[u+i]=udg[u-i+n]=1;cnt++;dfs(u+1);cnt--;col[i]=dg[u+i]=udg[u-i+n]=0;}}
}
int main()
{cin>>n>>a>>b;a--,b--; //题目从1~n,我们默认0~n-1,坐标偏移一下for(int i=-1;i<=1;i++) //把皇帝的地盘提前标记好{for(int j=-1;j<=1;j++){int x=a+i,y=b+j;if(x>=0 && x<n && y>=0 && y<n) st[x][y]=1;}}dfs(0);cout<<ans;return 0;
}