回溯算法之N皇后问题

问题描述

什么是皇后问题(有一定了解可以直接跳过这个部分看求解部分哦)

八皇后问题（英文：Eight queens），是由国际西洋棋棋手马克斯·贝瑟尔于1848年提出的问题，是回溯算法的典型案例。
问题表述为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。如果经过±90度、±180度旋转，和对角线对称变换的摆法看成一类，共有42类。计算机发明后，有多种计算机语言可以编程解决此问题。

一起看看经典教材 计算机算法设计与分析 对该问题的描述：

在 n × n 棋盘上放彼此不受攻击的n个皇后。
按照国际象棋规则，皇后可以攻击 同行、同列、同一斜线 的棋子。
等价于在 n × n 格的棋盘上放置 n 个皇后，任何 2 个皇后不放在 同一行 或 同一列 或 同一斜线 上。

解题思路

由于皇后的位置受到上述三条规则约束，我们必须通过一些技术手段来判断当前皇后的位置是否合法。

1.皇后的编号从 0 ~ N - 1 （N表示皇后的数量），这样编号的想法很简单：数组下标从0开始（这样方便后续对其位置的说明）。

2.使用一维数组 putInf 对每一行皇后的存放位置进行保存，因此得到解向量 (putInf[0], putInf[1], putInf[3], … , putInf[N - 1])，putInf[i] 表示第 i 个皇后被放置到了第 putInf[i] + 1 列上（putInf数组中存储的是列号，范围为 0 ~ N - 1）;

3.第二个条件：各皇后不同列， N 皇后放在 N x N 的棋盘上，那么每一列最多且必须放置一个皇后，这里我用了一个 used数组 对每一列的摆放情况进行记录， used[i] = true 表示第 i 列已经放置了皇后，used[i] = false 表示第i列暂未放置皇后，这样我们可以保证不在一列上放置多个皇后，也就能满足 各皇后不同列 的规则。

4.各皇后不能处于同一对角线位置：假设两皇后位置坐标分别为(i, j) 、（l, k），那么根据直线斜率公式：

(i - l) / (j - k) = 1 求解得 i - l == j - k ①
(i - l) / (j - k) = -1 求解得 i - l == k - j ②
这两种情况出现时表明处于同一对角线，那么要满足摆放规则就必须满足
| i - l | != | j - k | （“| |” 表示绝对值）

解空间树

解空间树（排列树）

实现代码

#include <iostream>
#include <vector>
using namespace std;#define N 4 //N皇后
vector<int> putInf;//每一行皇后的置放位置情况
//不同行 不同列 不同斜线 |ri - rj| != |ci - cj| 第1行与
vector<int> used(N, 0);//每一列只能有一个皇后，记录每一列的状态
vector<vector<int>> ans;//存储可行方案
int curRow = 0;//当前待放皇后的行数/*            正置放皇后行↓ 置放列↓              */
bool judgeLegalPut(int& curRow, int col) {//判断在curRow行的col列放置皇后是否合法for (int i = curRow - 1; i >= 0; i--) {//我们的解空间树已经去除一行一列置放相同元素//（每一个皇后被放在不同行以及不同列）的情况//因此我们只需要判断皇后是否成斜线即可if (curRow - i == abs(col - putInf[i])) {//当前位置与之前的皇后处于同一斜线上return false;}}return true;
}void queensAssign(int curRow) {if (curRow >= N) {//递归到叶子节点，递归结束，收集结果ans.push_back(putInf);return;}//i : 当前行皇后准备放的列数for (int i = 0; i < N; ++i) {//curRow行i列的位置if (used[i]) continue;//位置被使用过，直接跳过 //这样满足了不处于同一列的显条件 类似于全排列if (judgeLegalPut(curRow, i)) {//当前位置置放与之前不冲突 将皇后加入used[i] = true;putInf.push_back(i);queensAssign(curRow + 1);used[i] = false;//撤销之前的状态putInf.pop_back();}}
}void printChessBoard(vector<int>& vec) {//输出模拟棋盘cout << endl;for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {if (j != vec[i])cout << "○";elsecout << "●";}cout << endl;}cout << endl;
}
/// <author>
/// nepu_bin
/// <博客域名>
/// bincode.blog.csdn.net
int main() {queensAssign(0);int n = 1;cout << N << "皇后问题,方案如下:\n" << endl;for (vector<vector<int>>::iterator it = ans.begin(); it != ans.end(); it++) {cout << "第" << n++ << "种放置方案, 皇后被放于 " << endl;for (int i = 0; i < it->size(); i++) {cout << (*it)[i] + 1 << "  ";}cout <<"列" << endl;cout << endl << "棋盘布局如下↓" << endl;printChessBoard(*it);}return 0;
}

运行效果

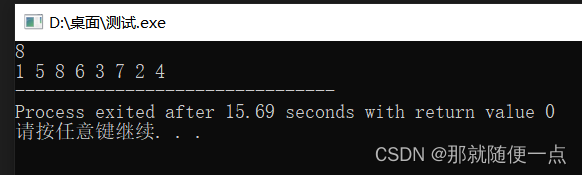
四皇后问题运行截图：
四皇后求解

通过修改宏定义 N 可以得到不同数量皇后问题的解答~~~
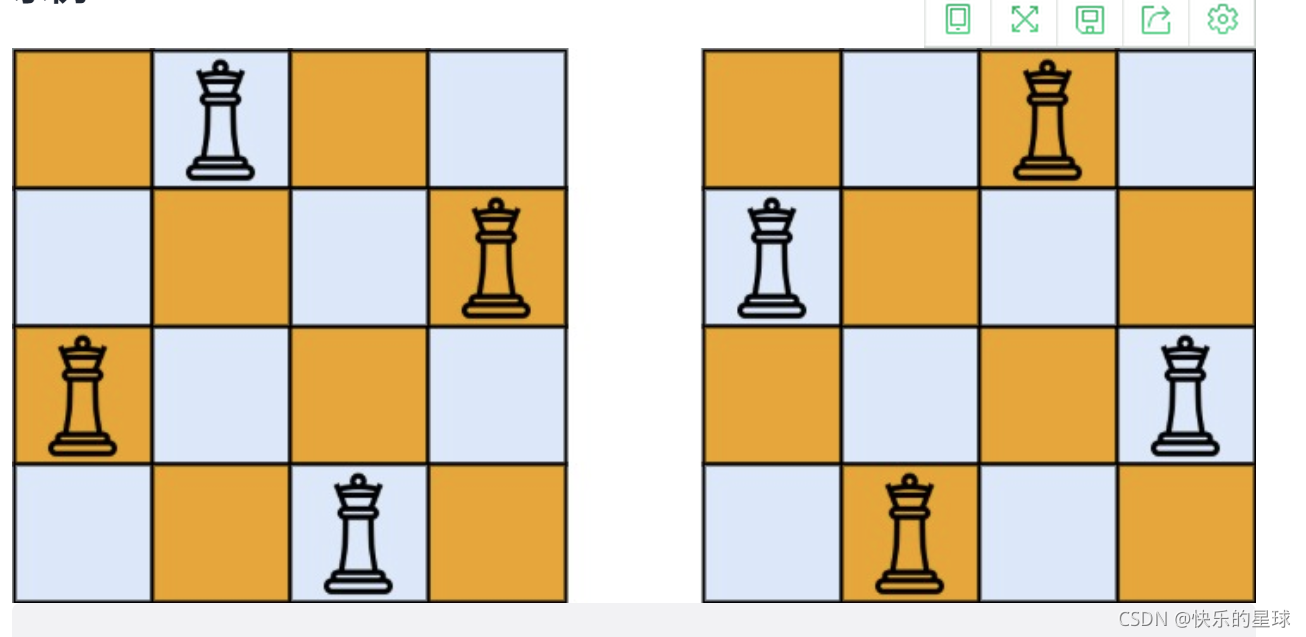
八皇后求解（部分解）：

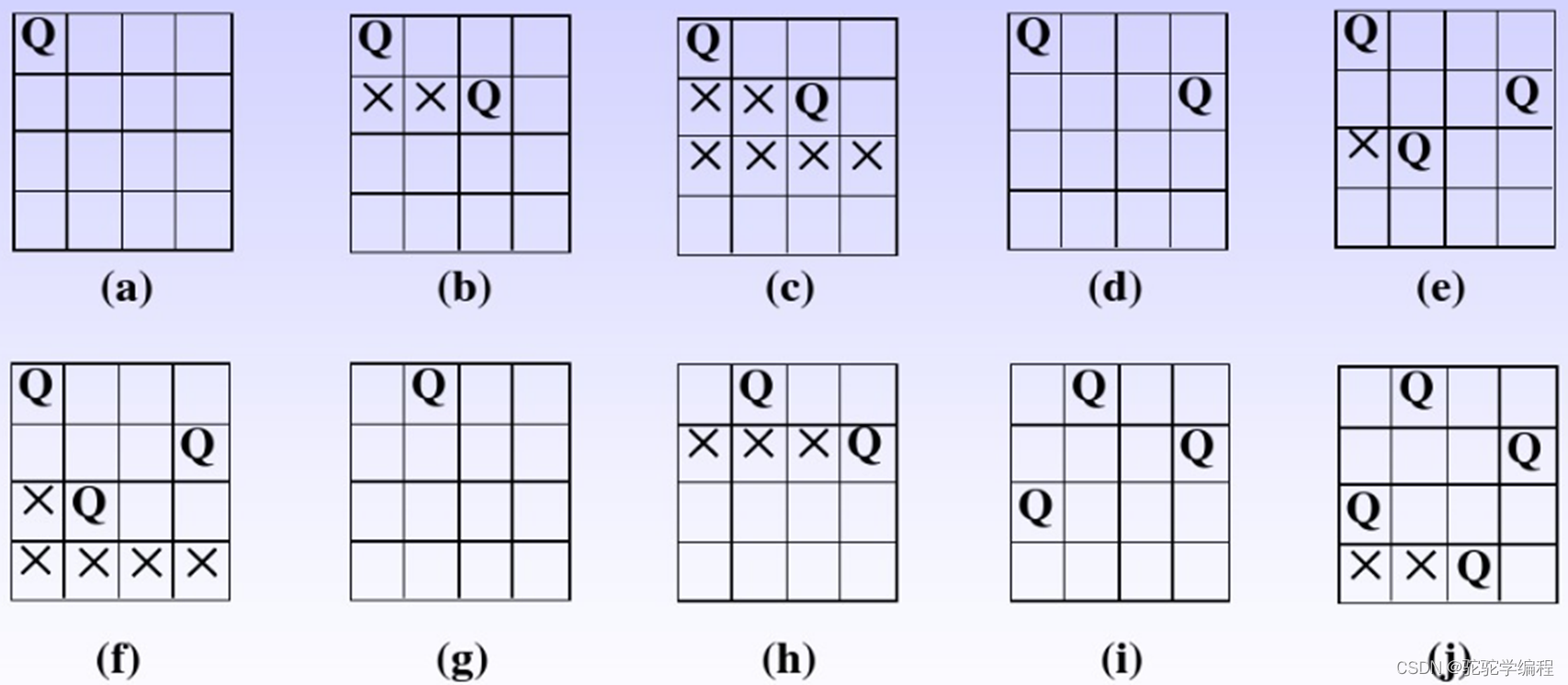
子集树与排列树

附上子集树 and 排列树的定义在这里插入图片描述

在了解过该问题之后便可以开始着手力扣上的N皇后问题，在这里贴一下实现代码：

LeetCode必刷经典: n 皇后问题

n 皇后问题，研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

链接：https://leetcode-cn.com/problems/n-queens
思路与上面完全一致，直接上实现代码：

class Solution {
public:vector<vector<string>> res;vector<int> put;//记录每个皇后放置的位置:i行put[i]列vector<string> solution;vector<bool> haveQ;//记录每一列位置上皇后的摆放情况//推导解空间树: 排列树、解集树//N皇后问题为排列树结构，每个皇后都需要放置 depth变量记录当前正摆放皇后的位置void dfs(int depth, int& n) {if (depth >= n) {res.push_back(solution);return;//此时已经完成所有皇后的摆放}for (int i = 0; i < n; i++) {//i表示列值if (haveQ[i]) continue;//当前列已经有皇后haveQ[i] = true;solution[depth][i] = 'Q';put[depth] = i;int j;//当前列无皇后，试探性摆放for (j = 0; j < depth; j++) {//检测前 depth - 1行是否发生冲突if (abs(j - depth) == abs(put[j] - i))break;}if (j >= depth) {//检测通过，继续深入dfs(depth + 1, n);}//检测失败，撤销之前的操作haveQ[i] = false;solution[depth][i] = '.';}}vector<vector<string>> solveNQueens(int n) {if (n == 1) return { {"Q"} };string str;str.assign(n, '.');//初始化n个'.'的字符串//保证横行纵行、斜线都不存在皇后//abs(y - cury) = abs(i - curi)haveQ.resize(n, false);solution.resize(n, str);put.resize(n, -1);//初始化3个容器dfs(0, n);return res;}
};

在这里的巧妙之处是：

利用了循环的顺序性消除了第一层限制: 同一行中不可以存在两个皇后，由于是顺序遍历，依次摆放皇后且每次只放置一个，因此该条件我们很容易实现。
第二个条件是同一列上不可以有两个及以上的皇后，在代码中使用了put数组，记录了每个皇后的摆放位置，利用了哈希映射的原理(put数组的下标( 0~put.size - 1) 对应着每个皇后，下标对应存储的值则表示了此位皇后摆放在了哪一列，打个比方: 下标i表示了第i位皇后(假设皇后的编号从零开始)， put[i]则表示第i位皇后被放在了put[i] 列；这么做的好处是为了实现有哈希表一样的查询效率O(1)。
第三条限制则是在回溯算法的核心部分体现：

//当前列无皇后，试探性摆放for (j = 0; j < depth; j++) {//检测前 depth - 1行是否发生冲突if (abs(j - depth) == abs(put[j] - i))break;}if (j >= depth) {//检测通过，继续深入dfs(depth + 1, n);}//检测失败，撤销之前的操作haveQ[i] = false;solution[depth][i] = '.';