相关文章
线性代数学习笔记——第九十讲——化二次曲面为标准方程
1. 用正交变换化二次型为标准型的方法 2. 化二次曲面为标准方程示例1 3. 化二次曲面为标准方程的一般方法 4. 化二次曲面为标准方程的示例2 5. 化二次曲面为标准方程的示例3
曲面研究的两个基本问题、旋转曲面、柱面、二次曲面
曲面及其方程
曲面方程概念
F(x,y,z)0就是曲面的方程 例如球面方程可以表示为
旋转曲面 母线:平面曲面 轴: 例如 绕哪一个轴旋转,哪一个轴就不变,另外一个量变成正负根号下平方和 总结规律
柱面
…
解析几何 曲线与二次曲面 曲面方程与坐标变换(2.1,2.2)
一.曲面的方程(2.1) 1.柱面: 2.锥面: 3.旋转面:
二.坐标变换(2.2) 1.平面坐标轴旋转: 2.空间坐标轴变换: 3.欧拉角(Euler Angles):
利用正交变换判断二次曲面类型
利用正交变换判断二次曲面类型 正交变换是欧式空间保持向量内积不变的线性变换。不仅保持向量的长度不变,而且还保持向量 的夹角不变。二维或三维空间中的旋转变换、关于某一条直线或平面的对称变换都是正交变换.投影变换、平移变换不是正交变换…
TikZ作图:九种二次曲面(附代码)
如何用TikZ/pgfplots宏包绘制《解析几何》中的二次曲面图像? 本文将逐一给出示例代码。
导言区设置如下:
\documentclass[border{1.2cm 0.1cm 1.2cm 0.1cm}]{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{patchplots}
\usepgfplotslibrary…
【高等数学】二次曲面直观几何形态展示
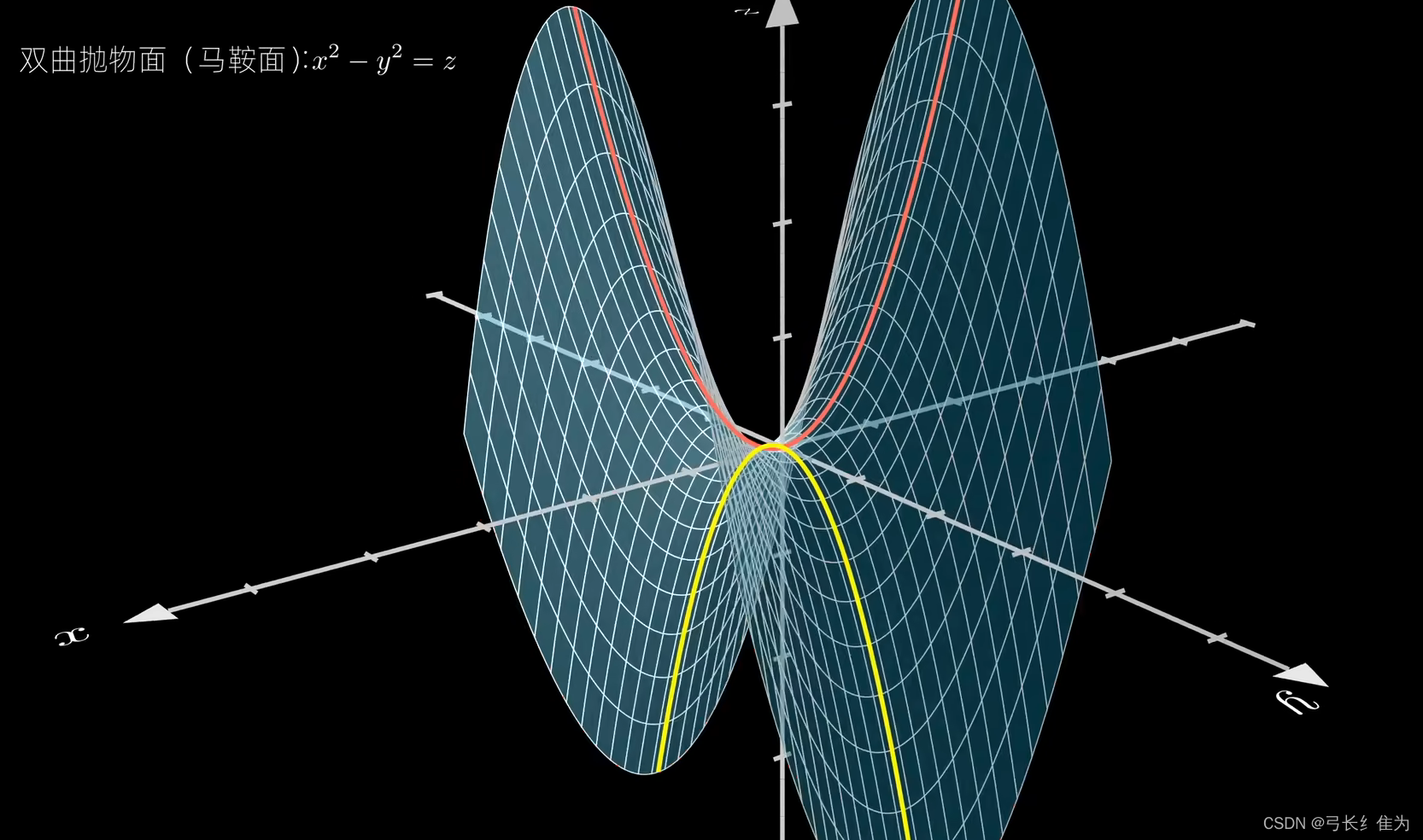
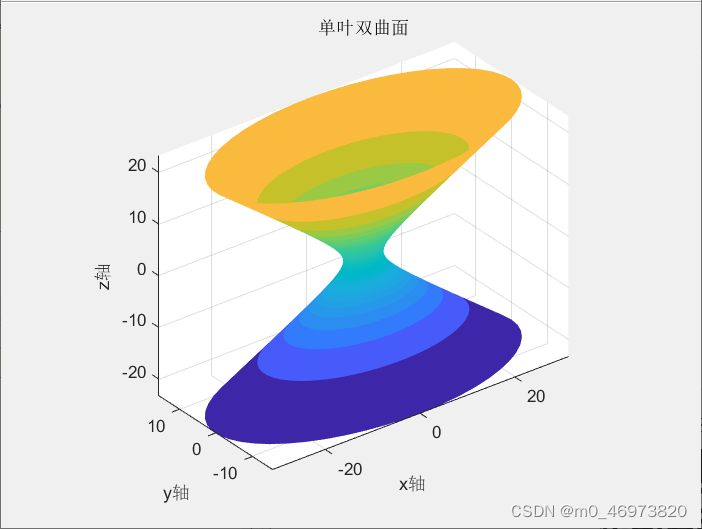
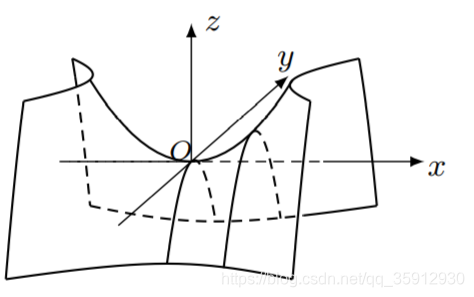
一、圆柱面 二、椭圆柱面 三、 双曲柱面 四、抛物柱面 五、圆锥面 六、椭圆锥面 七、球面 八、椭球面 九、椭圆抛物面 十、单叶双曲面 十一、双叶双曲面 十二、双曲抛物面(马鞍面)
数分下第5讲(8.3节) 二次曲面方程和曲线方程
第3.1讲 二次曲面方程和曲线方程
本讲是空间解析几何中的曲面和曲线方程,要求掌握二次曲面的生成方法和画图。 文章目录 第3.1讲 二次曲面方程和曲线方程学习要点一、二次曲面方程1、球面方程2、柱面方程:缺少一个变量3、旋转曲面(旋转&…
【学习记录】二次曲线、二次曲面、对偶二次曲线、对偶二次曲面
一、二次曲线与对偶二次曲线
最近在看基于椭球体的物体SLAM过程中,经常涉及到椭球体的空间几何知识,这里先补充一下一些空间几何相关的基础,参考链接。 椭球体本身属于二次曲面的一种,二次曲面是对空间形状的描述,属于…
空间二次曲面数据拟合算法推导及仿真分析
在上一篇的博客球面数据拟合算法简介中,笔者详细介绍了关于空间球面数据拟合的算法公式推导并给出了相应的Matlab代码及其仿真分析。本次笔者将上面这一情况进行更一般的推广,即取消了球面数据这一限制,数据可以是椭球面形式的,也…
通过Python绘制九种二次曲面
二次曲面
python中绘制三维图需要将坐标系声明为3d。
球面方程为 x 2 y 2 z 2 R 2 x^2y^2z^2R^2 x2y2z2R2
写为极坐标形式为 x R sin θ cos φ y R sin θ sin φ z R cos θ \begin{aligned} x&R\sin\theta\cos\varphi\\ y&R\sin\theta\sin\…
解析几何:第六章 二次曲面(1)球面 椭球面 双曲面
1.球面
1.球面方程,球心与半径 图形 方程 球心和半径 1 标准方程: xyzR 2 参数方程 (φ为经度,θ为纬度) 3 球面坐标方程 rR 球心:G(0,0,0) 半径:R 1 (x-a)(y-b)(z-c)R 2 参数方程&a…
解析几何:第六章 二次曲面(2)抛物面 二次锥面 柱面 一般二次曲面
4 抛物面
1.椭圆抛物面 (1)标准方程 (2)基本元素
*顶点 O(0,0,0)
*主轴 Z轴
*主平面 OYZ平面:x0;OZX平面:y0 (3)当ab时,椭圆抛物线面是由…
二次曲面标准方程和分类记忆方法(更新)
二次曲面标准方程和分类记忆方法 一类曲面-球面:圆球面,椭球面
1、球面 球面方程最简单。
描述:中心在(x0,y0,z0),半径是r的所有点(x, y, z)的集合
令x00;y00;z00;得到中心在坐标原点的球面 …
MATLAB 画常见二次曲面汇总
一、螺旋线
1.静态螺旋线
a0:0.1:20*pi; hplot3(a.*cos(a),a.*sin(a),2.*a,b,linewidth,2); axis([-50,50,-50,50,0,150]); grid on set(h,erasemode,none,markersize,22); xlabel(x轴);ylabel(y轴);zlabel(z轴); title(静态螺旋线); 2.动态螺旋线
t0:0.1:10*pi;
i1;
hplo…
MATLAB-二次曲面
柱面:圆柱面;椭圆柱面;双曲柱面;抛物柱面
锥面:圆锥面;椭圆锥面
锥球面;球面
椭圆抛物面;
单叶双曲面;双叶双曲面
双曲抛物面;
旋转抛物面,…
二次曲面标准方程和分类记忆方法
二次曲面标准方程和分类记忆方法 一类曲面-球面:圆球面,椭球面
1、球面 球面方程最简单。
描述:中心在(x0,y0,z0),半径是r的所有点(x, y, z)的集合
令x00;y00;z00;得到中心在坐标原点的球面 …
解析几何 曲线与二次曲面 二次曲面的分类(2.3)
一.二次曲面 二.二次曲面的旋转不变量 三.特征方程和特征根 1.特征根(特征值)与主方向(特征方向,特征向量): 2.不同直角坐标系下的主方向: 3.二次曲面的标准形式: 引理1:非零实对称矩阵 D D D的特征根全是实数 引理2:非零实对称矩阵 D D D的3个特征根至少有…
几何-九种二次曲面类型
(一)椭圆锥面 (1)把z平方看成一个一直变大的常数,那么可以看出延z方向,是一个一直变大的椭圆。
(2)把一个x或y赋予0,显然是一个两条关于原点对称的直线。
由上即可判断…