§1.球面
1.球面方程，球心与半径
| 图形 | 方程 | 球心和半径 |
| | 1° 标准方程： x²+y²+z²=R² 2° 参数方程
（φ为经度，θ为纬度） 3° 球面坐标方程 r=R | 球心：G(0,0,0) 半径：R
|
|
| 1° (x-a)²+(y-b)²+(z-c)²=R² 2° 参数方程：
（φ为经度，θ为纬度） | 球心：G(a,b,c) 半径：R
|
|
| x²+y²+z²+2px+2qy+2rz+d=0 p²+q²+r²>d | 球心：G(-p,-q,-r) 半径：
|
2.球面的切平面与法线
若以平面P通过球面上一点M，且垂直与半径GM，则称平面P为球面在点M的切平面。直线MG称为球面在点M的法线。
设球面方程为x²+y²+z²+2px+2qy+2rz+d=0
则球面在点的切平面方程为x0x+y0y+z0z+p(x+x0)+q(y+y0)+r(z+z0)+d=0
球面在点的法线方程为
3.两个球面的交角，两个球面正交的条件
（1）两个球面的交角是指它们在交点处的两个切平面的夹角。
设两个球面S1:x²+y²+z²+2p1x+2q1y+2r1z+d1=0
S2:x²+y²+z²+2p2x+2q2y+2r2z+d2=0
记它们的交角为θ，则有 
上式中不包含交点的坐标，所以两个球面在交线上各点的交角都相等。
（2）由交角余弦表达式，可得到两个球面正交的条件为
2p1p2+2q1q2+2r1r2-d1-d2=0
§2 椭球面
1. 椭球面方程
（1）标准方程：
（a,b,c>0)
参数方程：
（角φ，θ如图所示）
（2）特殊情况
- 当a=b时为旋转椭球面
它是OXZ平面上曲线(椭圆)： 绕Z轴旋转面得到的
注：b=c或a=c的情况类似
- 当a=b=c时为球面：x²+y²+z²=a²
2. 基本元素
- 顶点：
- 主轴：
依照a,b,c的大小，分别称为长轴、中轴、短轴。主轴之半径称为半轴，类似的有长半轴、中半轴、短半轴之分。
- 主平面 OXY平面：z=0 ; OYZ平面：x=0 ; OZX平面：y=0
- 中心 O(0,0,0)
- 直径：通过中心的弦
- 直径平面：通过中心的平面
§3 双曲面
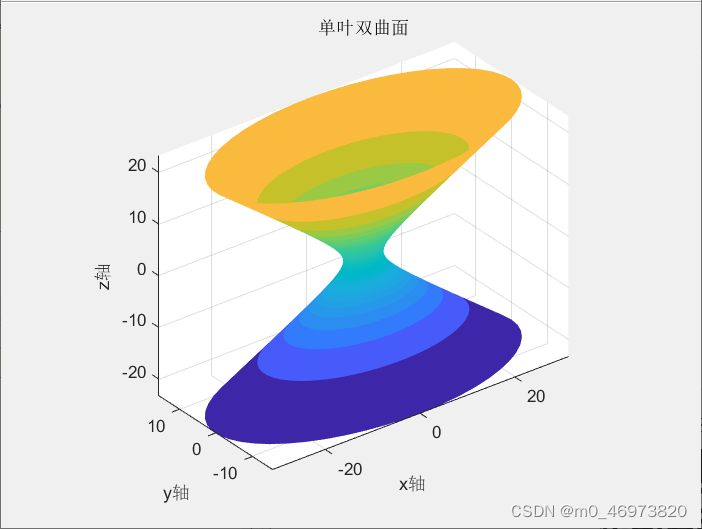
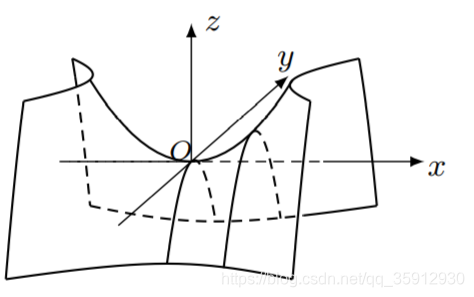
1.单叶双曲面
(1)标准方程
(a,b,c>0)
(2) 基本元素
·顶点 
·主轴 
（依照a,b的大小分别称为实长轴和实短轴）
·中心 O(0,0,0)
·主平面 OXY平面：z=0 ; OYZ平面: x=0; OZX平面：y=0
(3) 直纹面母线方程
单叶双曲面是直纹面，且通过曲线面上每一点均有两条直母线。单叶双曲面上的两族直母线方程为：
与
（4) 平面与单叶双曲面的交线
·平行于Z轴的平面与单叶双曲面的交线都是双曲线，特殊情况为一对相交直线。
·垂直于Z轴的平面与单叶双曲面的交线都是椭圆，特别，OXY平面与曲面的交线：
称为单叶双曲面的腰圆.(如右图）
2. 双叶双曲面
（1）标准方程
（a,b,c>0)
(2)基本元素
·顶点 C,C´(0,0,±c)
·主轴 （依照a,b大小分别称为实长轴和实短轴）
·中心 O(0,0,0)
·主平面 OXY平面：z=0 ; OYZ平面：x=0; OZX平面：y=0
（3）当a=b时为旋转双曲面
当a=b时，双叶双曲面是由OXZ平面上的双曲线
绕Z轴旋转得到的。
（4）平面与双叶双曲面的交线
·平行于Z轴的平面与双叶双曲面的交线均为双曲线
·垂直于Z轴的平面z=k(|k|≥c)与双叶双曲面的交线都是椭圆。特殊情况(|k|=c)为一点。
from: http://202.113.29.3/nankaisource/mathhands/
