§4 抛物面
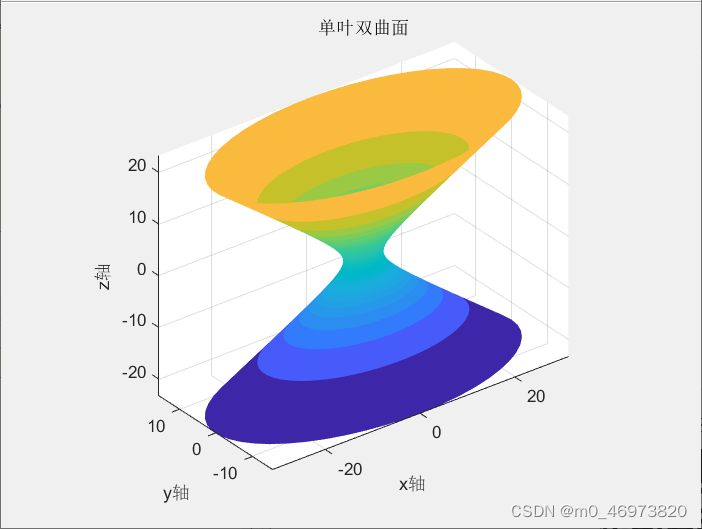
1.椭圆抛物面
(1)标准方程
(2)基本元素
*顶点 O(0,0,0)
*主轴 Z轴
*主平面 OYZ平面:x=0;OZX平面:y=0
(3)当a=b时,椭圆抛物线面是由OZX平面上的抛物线绕Z轴旋转得到的
(4)平面与椭圆抛物面的交线
*平行于Z轴的平面与椭圆抛物面的交线是抛物线
*垂直于轴的平面z=k()与椭圆抛物线的交线是椭圆,特殊情况(k=0)为一点
2.双曲抛物面
(1)标准方程

(2)基本元素
*顶点 O(0,0,0)
*主轴 Z轴
*主平面 OYZ平面:x=0;OZX平面:y=0
(3)直纹面母线方程
双曲抛物面是直纹面,且通过曲面上每一点均有两条直母线。
双曲抛物面的两族直母线方程为:
与

§5 二次锥面与柱面
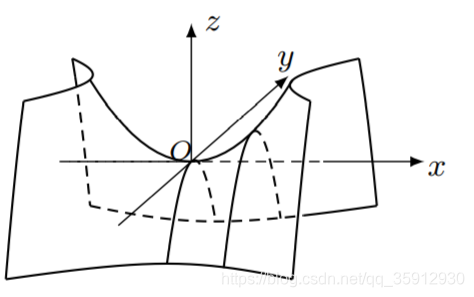
1.锥面的定义
设Γ为平面π上一条曲线,V为π外一点。当动点P沿着Γ运动时,直线VP(直线l) 的轨迹称为以V为顶点,Γ为底线,l为母线的锥面(如右图)。
锥面是直纹面。
2.椭圆锥面
(1)标准方程![]()
(2)基本元素(如右图)
- 顶点 O(0,0,0)

- 主轴 Z轴
- 准线Γ

(3)当a=b时为旋转曲面
当a=b时,椭圆锥面为圆锥面,它是OZX平面上的直线![]() 绕Z轴旋转得到的。
绕Z轴旋转得到的。
(4)平面与椭圆锥面的交线
- 平行于OXY的平面:z=k与椭圆锥面的交线是椭圆:


特别,平面Z=0与曲线交于原点O
- 平行于OYZ或OZX的平面与椭圆锥面的交线是双曲线(k≠0)或一对交于O的直线(k=0)

(5)椭圆锥面是双叶双曲面和单叶双曲面的渐近锥面
椭圆锥面:![]()
双叶双曲面:![]()
单叶双曲面:![]() (a,b,c>0)
(a,b,c>0)
- 三个曲面与平面z=k的交线均为椭圆,当k→∞时,三个椭圆无限接近,即三个曲面无限接近。
- 通过Z轴的每个平面与双曲面的交线为一对共轭双曲线,与锥面的交线为两条直线,即是这对双曲线的渐近线。

3.柱面的定义
设Γ是一空间曲线,l是一条固定的直线。与Γ相交而且与l平行的直线集合所构成的曲面称为柱面。称Γ为柱面的准线,柱面上与l平行的直线称为母线。
显然,柱面S与可视为l沿Γ平行运动而生成的曲面。
柱面是直纹面。
4.椭圆柱面,双曲柱面,抛物柱面
| 名称 | 图形 | 方程 | 准线与母线 | 与平面交线 |
| 椭圆 柱面 |
|
当a=b时,为圆柱面: x2+y2=a2 | 准线: 母线方向数:(0,0,1) | 与平行于OXY平面z=k的交线都是椭圆:
|
| 双曲 柱面 |
|
| 准线: 母线方向数:(0,0,1) | 与平行于OXY平面z=k的交线都是双曲线:
|
| 抛物 柱面 |
|
| 准线: 母线方向数:(0,0,1) | 与平行于OXY平面z=k的交线都是抛物线:
|
§6 一般二次曲面
1.一般二次曲面的方程
x,y,z的二次方程
![]()
所表示的二次曲面称为一般二次曲面。
2.二次曲面的一般性质
(1)直线与二次曲面的交点
一直线与一个二次曲面交于两点(实的,虚的,重合的);或者这直线全在曲面上,此时称它为二次曲面的直母线或母线。
(2)平面与二次曲面的交线
任一平面与一个二次曲面的交线为一个二次曲线。
(3)二次曲面的直径平面与中心
一个二次曲面的平行于已知方向的弦的中点在一个平面上,称为直径平面,它平分某一组平行弦,设已知方向的方向数为l,m,n,则直径平面的方程为
(al+hm+gn)x+(hl+bm+fn)y+(gl+fm+cn)z+(pl+qm+rn)=0
或改写为
(ax+hy+gz+p)l+(hx+by+fz+q)m+(gx+fy+cz+r)n=0
当l,m,n变动时,这个方程表示一个平面把,由此,二次曲面的直径平面组成一个平面把,平面把内任意平面都通过下列平面的交点:
ax+hy+gz+p=0
hx+by+fz+q=0
gz+fy+cz+r=0
如果交点不在曲面上,则称它为二次曲面的中心;如果交点在曲面上,则称它为二次曲面的顶点。凡有中心的二次曲面称为有心二次曲面,其余的都称为无心二次曲面。
(4)二次曲面的主平面与主轴
如果直径平面垂直于被它所平分的弦,则称为主平面(对称平面),每个二次曲面至少有一个实主平面,非旋转二次曲面的任两主平面是互相垂直的,它们的交线为主轴。
(5)二次曲面的圆截面
如果一个平面与一个二次曲面的交线为一个圆,则称该平面为曲面的圆截面。
如果二次曲面不是球面,则通过空间中一点,二次曲面有六个圆截面;其中一般有两个实圆
截面,四个虚圆截面;而且六个圆截面中有几个是重合的。
3.二次曲面的切面与法线
二次曲面在一点M(x0,y0,z0)的切面方程为
ax0x+by0y+cz0z+f(y0z+z0y)+g(z0x+x0z)+h(x0y+y0x)+p(x+x0)+q(y+y0)+r(z+z0)+d=0
在点M与二次曲面的切面垂直的直线称为曲面在点M的法线,它的方程可写为
![]()
4.二次曲面的不变量
由二次曲面的一般方程
![]() (1)
(1)
的系数组成的下列四个函数:

![]()
称为二次曲面的不变量,即经过坐标变换后,这些量是不变的,行列式Δ称为二次方程(1)的
判别式。
5.二次曲面标准方程及形状
| 不变量 | 坐标变换后的方程 | 曲线形状 | ||
| D≠0 有心二次曲面 | Δ>0 | 式中A,B,C,为特征方程 的三个特征根 | A,B,C异号时为单叶双曲面。 A,B,C同号时无轨迹 | |
| Δ<0 | A,B,C同号时为椭球面 A,B,C异号时为双叶双曲面 | |||
| Δ=0 | A,B,C同号时无轨迹 A,B,C异号时为二次锥面 | |||
| D=0 无心二次曲面 | Δ<0
| | 椭圆抛物面 (A,B都是正的时,根号前取负号;A,B都是负的时,根号前取正号) | |
| Δ>0 | 双曲抛物面 | |||
| Δ=0 | J≠0 | | | |
| J=0 | | 抛物柱面 一对平行平面 无轨迹 一对重合平面 | ||
from: http://202.113.29.3/nankaisource/mathhands/