第3.1讲 二次曲面方程和曲线方程

本讲是空间解析几何中的曲面和曲线方程，要求掌握二次曲面的生成方法和画图。

学习要点

1、本章的核心问题是会根据曲面/曲线方程画图。
1、曲面方程两个题型：已知轨迹运动求曲面方程；已知方程画图形；
2、运动轨迹中，平面曲线L 绕z轴旋转运动时，z不变，y变成 +/- sqrt(x²+y²)。注意方程的变化。
3、在已知方程画图形题型中，有两种方法：平面截痕法、旋转变形法。
4、曲线方程有四个题型。

一、二次曲面方程

方程F(x,y,z)=0如果是三元二次方程，称为二次曲面，如球面x²+y²+z²=R²。平面称为一次曲面如x+ y -z +2=0。

1、球面方程

根据两点距离公式容易得出球面方程：（x-a）²+(y-b)²+(z-c)²=R²。一般表达式为 Ax²+Ay²+Az²+Dx+Ey+Fz+G=0。可以看出球面方程的特点：平方项系数相同、无交叉项。通过配方法可以得出其标准形式。

2、柱面方程：缺少一个变量

F(x,y)=0 表示母线平行于z的柱面，准线为 平面曲线C:F(x,y)=0.

3、旋转曲面（旋转）

平面曲线绕其平面上一条直线旋转一周，称为旋转曲面，其中定直线为轴，动曲面为母线。

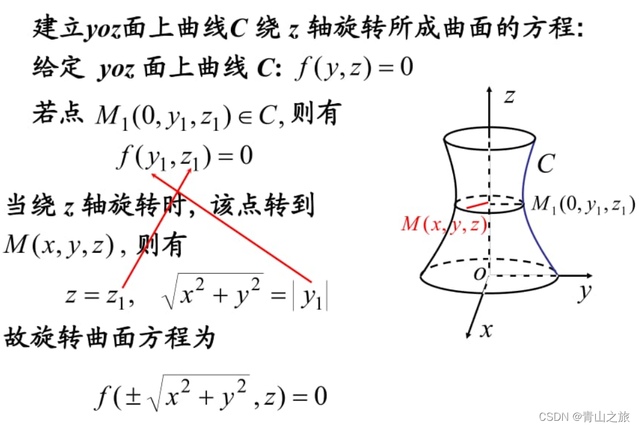
4、二次曲面（旋转后拉伸变形）

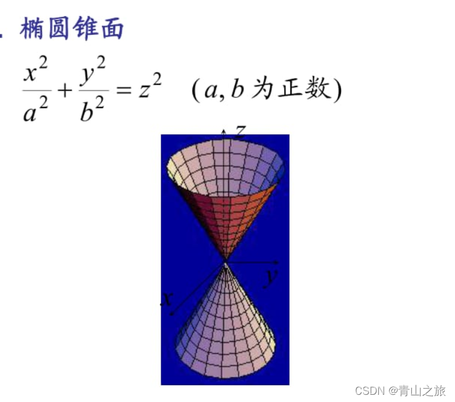
（1）椭圆锥面

采用截痕法判断曲面形状。

（2）椭球面

用平面截痕法进行分析。

也可以用运动轨迹法分析其图形。把xOz平面上椭圆x²/a² + z²/c²=1 绕z轴旋转，得到x²+y²)/a² +z²/c²=1，然后做拉伸变形y1 = b/a * y，带入之后得到椭球面。

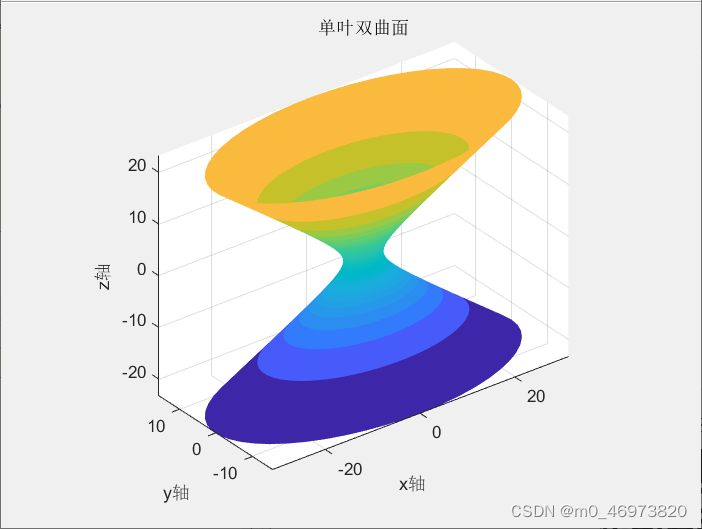
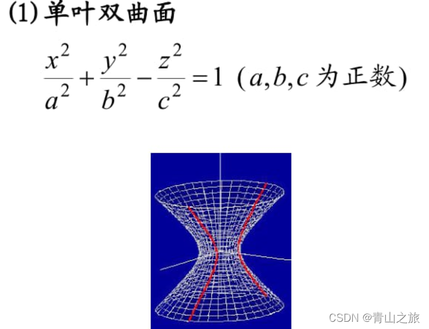
（3）单叶双曲线

双曲线先绕z轴旋转，再在y轴方向上做伸缩变形，得到单叶双曲线。

（4）双叶双曲面

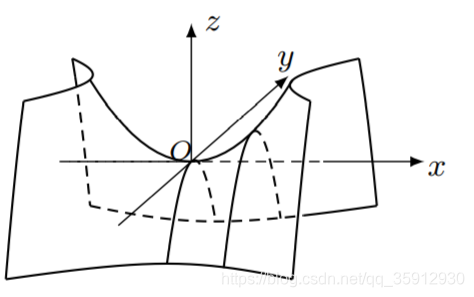
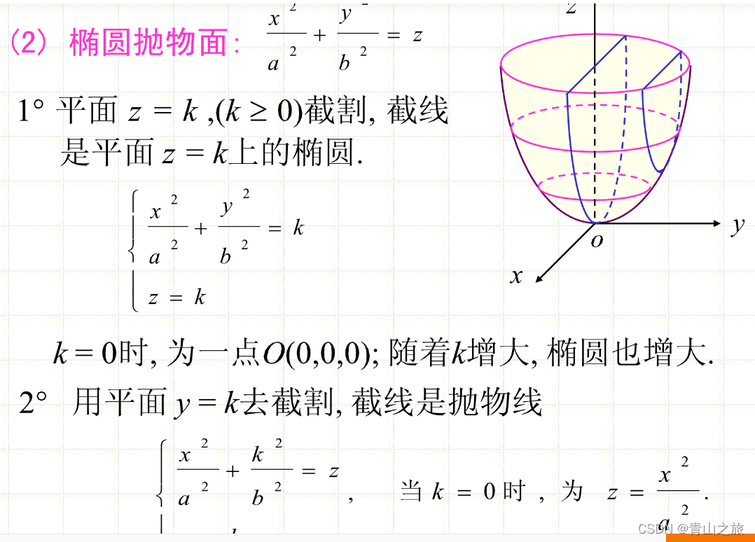
（5）椭圆抛物面/双曲抛物面

二、<曲面方程>考点题型

1、题型1：旋转运动写曲面方程【解法：掌握旋转、变形对应的方程变化形式】

2、题型2：已知曲面方程画几何图形【解法：熟悉典型函数对应的运动轨迹】

二、曲线方程

1、曲线的一般方程（曲面相交）

2、曲线的参数方程

3、曲面的参数方程

利用z轴方向平面截面中，旋转形成的圆周关系。

4、曲线在曲面上的投影

曲线在坐标面上的投影，在重积分、曲面积分中会用到。

三、<曲线方程>考点题型

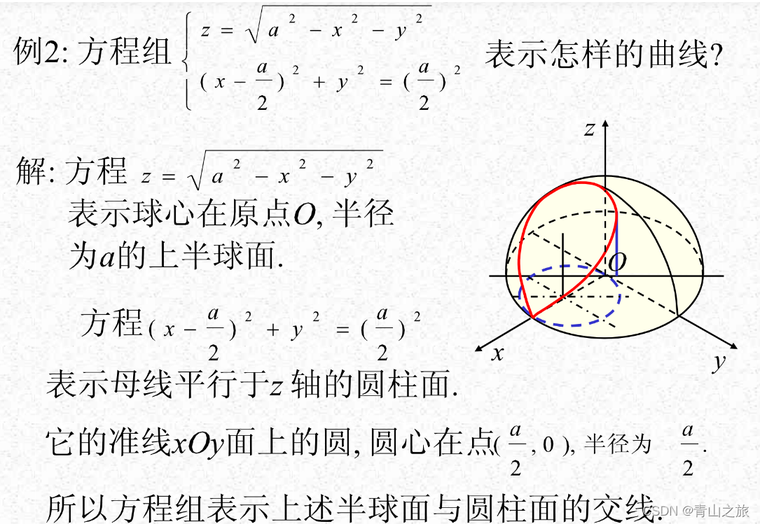
1、曲线题型1：根据曲线一般方程画图【解法：熟悉柱面球面平面方程】

2、曲线题型2： 一般方程与参数方程转化【解法：利用三角函数】

技巧解法： 利用三角函数

3、曲线题型3：旋转曲面参数方程求法【解法：利用三角函数和截面法中的旋转关系】

4、曲线题型4：曲线投影方程求解【解法：消元后柱面】