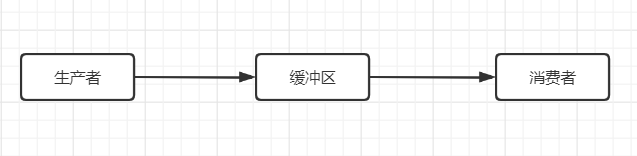
【Java总结】生产者消费者模型

article/2025/9/28 7:35:28

生产者消费者模型主要结构如下，是一个典型的线程同步的案例。下面就来使用java做几种线程同步的方式来实现以下该模型

在这里插入图片描述

确保一个生产者消费者模型的稳定运行的前提有以下几个

  • 生成者应该具备持续生成的能力
  • 消费者应该具备持续消费的能力
  • 生产者的生成和消费消费有一定的阀值，如生成总量到100需要停止生产，通知消费；消费到0的时候停止消费开始生产；

  • wait,notify方案
  • ReentrantLock的实现
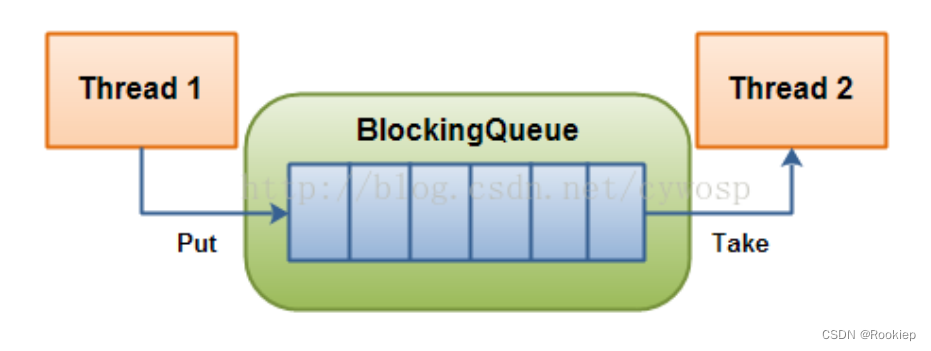
  • 阻塞队列的实现

wait,notify方案

wait,notify方案 主要是通过，使用对象的wait方法和notify方法来实现线程的切换执行。其中我们可以看到对象的wait和notify或者notifyAll方法都是调用native的对应的方法来处理，追溯到最后也还是控制cpu进行不同的时间片的切换

下面这个例子比较简单，模拟一个生产速度大于消费速度的这样一个案例，在生产到阀值的时候停止生产通知消费者进行消费(wait)。消费者在消费到一定阀值的时候停止消费通知生产者进行生产(notifyall)

public class TestWaitNotifyConsumerAndProducer {/*当前生成数量*/static int currentNum = 0;/*最大生成数量*/static int MAX_NUM = 10;/*最小消费数量*/static int MIN_NUM = 0;/*wait和notify控制对象*/private static final String lock = "lock";public static void main(String args[]) {//创建一个生产者new Thread(new Producer()).start();//创建两个消费者new Thread(new Consumer()).start();new Thread(new Consumer()).start();}static class Producer implements Runnable {public void product() {while (true) {try {Thread.sleep(10);} catch (InterruptedException e) {e.printStackTrace();}synchronized (lock) {currentNum++;System.out.println("Producer now product num:" + currentNum);lock.notifyAll();if (currentNum == MAX_NUM) {try {lock.wait();} catch (InterruptedException e) {e.printStackTrace();}}}}}@Overridepublic void run() {product();}}static class Consumer implements Runnable {public void consume() {while (true) {try {Thread.sleep(1000);} catch (InterruptedException e) {e.printStackTrace();}synchronized (lock) {if (currentNum == MIN_NUM) {lock.notifyAll();continue;}System.out.println(new StringBuilder(Thread.currentThread().getName()).append(" Consumer now consumption num:").append(currentNum));currentNum--;}}}@Overridepublic void run() {consume();}}
}

ReentrantLock的实现

ReentrantLock 也是java.util.concurrent中显示锁的一种，允许同一个线程重复进入一段执行代码（递归），并且反复lock加锁。重复加锁相当于计数器累加，因此当一个线程想释放这个锁的时候就需要有对应的unlock执行。

如下这段代码依然是我们开篇讲到的生成和消费的模型，只是换了一种实现;这里特别注意的是可重入锁或者递归锁需要成对的出现lock和unlock否则执行Condition的await 或者signal的时候就可能如下抛出

java.lang.IllegalMonitorStateException

public class TestReentrantLockConsumerAndProducer {/*当前生成数量*/static int currentNum = 0;/*最大生成数量*/static int MAX_NUM = 10;/*最小消费数量*/static int MIN_NUM = 0;//创建一个锁对象private static Lock lock = new ReentrantLock();//缓冲区已空的变量private static final Condition emptyCondition = lock.newCondition();//缓冲区已满的变量private static final Condition fullCondition = lock.newCondition();public static void main(String args[]) {//创建一个生产者new Thread(new Producer()).start();//创建两个消费者new Thread(new Consumer()).start();new Thread(new Consumer()).start();}static class Producer implements Runnable {public void product() {while (true) {try {Thread.sleep(10);} catch (InterruptedException e) {e.printStackTrace();}lock.lock();currentNum++;System.out.println("Producer now product num:" + currentNum);if (currentNum == MAX_NUM) {emptyCondition.signal();try {fullCondition.await();} catch (InterruptedException e) {e.printStackTrace();}}lock.unlock();}}@Overridepublic void run() {product();}}static class Consumer implements Runnable {public void consume() {while (true) {try {Thread.sleep(1000);} catch (InterruptedException e) {e.printStackTrace();}lock.lock();if (currentNum == MIN_NUM) {fullCondition.signal();try {emptyCondition.await();} catch (InterruptedException e) {e.printStackTrace();}continue;}System.out.println(new StringBuilder(Thread.currentThread().getName()).append(" Consumer now consumption num:").append(currentNum));currentNum--;lock.unlock();}}@Overridepublic void run() {consume();}}
}

阻塞队列的实现

阻塞队列的实现本质上也还是基于可重入锁，只是进行了进一步的封装，有一个队列的数据结构

这里我们用到了一个数据结构LinkedBlockingDeque的双向队列的结构，当然我们使用任何一个阻塞队列都可以。这里主要用到阻塞队列超过最大容量的时候，自动阻塞等待;
这里使用了几个关键的方法peek,put,peekLast,take 这里大概看看相关源码。 这里源码我们不做过多解读，大概可以看到阻塞队列的内部实现也是依赖于可重入锁ReentrantLock，然后根据put和take的操作，动态的管理锁的获取和释放。

  	/** Maximum number of items in the deque */private final int capacity;/** Main lock guarding all access */final ReentrantLock lock = new ReentrantLock();/** Condition for waiting takes */private final Condition notEmpty = lock.newCondition();/** Condition for waiting puts */private final Condition notFull = lock.newCondition();public E peekFirst() {final ReentrantLock lock = this.lock;lock.lock();try {return (first == null) ? null : first.item;} finally {lock.unlock();}}public E peekLast() {final ReentrantLock lock = this.lock;lock.lock();try {return (last == null) ? null : last.item;} finally {lock.unlock();}}//take元素的时候执行，可见如果当队列内容为空的时候阻塞public E takeFirst() throws InterruptedException {final ReentrantLock lock = this.lock;lock.lock();try {E x;while ( (x = unlinkFirst()) == null)notEmpty.await();return x;} finally {lock.unlock();}}/*** Removes and returns first element, or null if empty.* 具体删除操作，当操作删除完成以后执行notFull.signal();释放notFull的阻塞*/private E unlinkFirst() {// assert lock.isHeldByCurrentThread();Node<E> f = first;if (f == null)return null;Node<E> n = f.next;E item = f.item;f.item = null;f.next = f; // help GCfirst = n;if (n == null)last = null;elsen.prev = null;--count;notFull.signal();return item;}/*** Links node as last element, or returns false if full.* 当执行成功添加时，释放notEmpty的信号*/private boolean linkLast(Node<E> node) {// assert lock.isHeldByCurrentThread();if (count >= capacity)return false;Node<E> l = last;node.prev = l;last = node;if (first == null)first = node;elsel.next = node;++count;notEmpty.signal();return true;}

public class TestBlockQueueConsumerAndProducer {/*最大生成数量*/static int MAX_NUM = 10;private static LinkedBlockingDeque mBlockQueue = new LinkedBlockingDeque<Integer>(MAX_NUM);public static void main(String args[]) {//创建一个生产者new Thread(new Producer()).start();//创建两个消费者new Thread(new Consumer()).start();//创建两个消费者new Thread(new Consumer()).start();}static class Producer implements Runnable {public void product() {while (true) {if (mBlockQueue.peek() == null) {try {Thread.sleep(1000);} catch (InterruptedException e) {e.printStackTrace();}for (int i = 1; i <= 10; i++) {try {mBlockQueue.put(i);System.out.println("Producer now product num:" + i);} catch (InterruptedException e) {e.printStackTrace();}}}}}@Overridepublic void run() {product();}}static class Consumer implements Runnable {public void consume() {while (true) {try {Thread.sleep(500);} catch (InterruptedException e) {e.printStackTrace();}Integer mLast = (Integer) mBlockQueue.peekLast();if (mLast != null && mLast == MAX_NUM) {try {int num = (Integer) mBlockQueue.take();System.out.println(new StringBuilder(Thread.currentThread().getName()).append(" Consumer now consumption num:").append(num));} catch (InterruptedException e) {e.printStackTrace();}}}}@Overridepublic void run() {consume();}}
}

http://chatgpt.dhexx.cn/article/PAX8qU6y.shtml

相关文章

【设计模式】生产者消费者模型

【设计模式】生产者消费者模型

带你轻松理解生产者消费者模型&#xff01;生产者消费者模型可以说是同步与互斥最典型的应用场景了&#xff01;文末附有模型简单实现的代码&#xff0c;若有疑问可私信一起讨论。 文章目录 一&#xff1a;为什么要使用生产者消费者模型&#xff1f;二&#xff1a;生产者消费者…
阅读更多...
模拟生产者消费者模型

模拟生产者消费者模型

生产者消费者是多线程很经典的一个模型 牵涉三个对象&#xff1a;仓库、生产者、消费者 仓库代表共享变量 生产者表示在仓库生产货物 消费者表示从仓库拿出货物 实现思路&#xff1a;利用synchronizedwait()notify() 对生产者消费者对应的操作用synchronized关键字保证线程安全…
阅读更多...
生产者消费者模型java实现

生产者消费者模型java实现

做题的时候遇到了生产者消费者问题&#xff0c;这个问题可以说是线程学习的经典题目了&#xff0c;就忍不住研究了一波。它描述是有一块缓冲区&#xff08;队列实现&#xff09;作为仓库&#xff0c;生产者可以将产品放入仓库&#xff0c;消费者则可以从仓库中取走产品。在Java…
阅读更多...
生产者消费者模型详解以及实现

生产者消费者模型详解以及实现

生产者消费者模式 我们先来看看什么是生产者消费者模式&#xff0c;生产者消费者模式是程序设计中非常常见的一种设计模式&#xff0c;被广泛运用在解耦、消息队列等场景。在现实世界中&#xff0c;我们把生产商品的一方称为生产者&#xff0c;把消费商品的一方称为消费者&…
阅读更多...
Java生产者消费者模型的五种实现方式

Java生产者消费者模型的五种实现方式

转自&#xff1a;https://juejin.im/entry/596343686fb9a06bbd6f888c 前言 生产者和消费者问题是线程模型中的经典问题&#xff1a;生产者和消费者在同一时间段内共用同一个存储空间&#xff0c;生产者往存储空间中添加产品&#xff0c;消费者从存储空间中取走产品&#xff0c…
阅读更多...
生产者消费者模型---详解及代码实现

生产者消费者模型---详解及代码实现

概念 生产者消费者模式就是通过一个容器来解决生产者和消费者的强耦合问题。生产者和消费者彼此之间不直接通讯&#xff0c;而通过阻塞队列来进行通讯&#xff0c;所以生产者生产完数据之后不用等待消费者处理&#xff0c;直接扔给阻塞队列&#xff0c;消费者不找生产者要数据…
阅读更多...
生产消费者模型

生产消费者模型

生产消费者模型中包含三个部分&#xff0c;生产者、消费者和交易场所。其中涉及如下的关系&#xff1a; &#xff08;1&#xff09;生产者和生产者之间的关系&#xff1a;由于生产者的生产面向的都是交易场所&#xff0c;所以生产者之间是存在竞争关系的&#xff0c;就像一家超…
阅读更多...
生产者-消费者模型

生产者-消费者模型

什么是生产者消费者模型 生产者 - 消费者模型&#xff08; Producer-consumer problem&#xff09; 是一个非常经典的多线程并发协作的模型&#xff0c;在分布式系统里非常常见。 这个模型由两类线程和一个缓冲区组成来组成 生产者线程&#xff1a;生产数据&#xff0c;并把…
阅读更多...
最长上升子序列和最长公共子序列

最长上升子序列和最长公共子序列

文章目录 文章目录 文章目录一、基本知识二、最长上升子序列1.朴素版2.二分版 三、最长公共子序列 一、基本知识 1.子串和子序列的区别&#xff1a; 子串必须连续,子序列可以不连续。 2.最长上升子序列(LIS)&#xff1a; 是指一个序列中最长的单调递增的子序列。 3.最长公共…
阅读更多...
求最长子序列及回溯

求最长子序列及回溯

D - 最长公共子序列问题 Description 给定两个序列 X{x1,x2,…,xm} 和 Y{y1,y2,…,yn}&#xff0c;找出X和Y的最长公共子序列。 Input 输入数据有多组&#xff0c;每组有两行 &#xff0c;每行为一个长度不超过500的字符串&#xff08;输入全是大写英文字母&#xff08;A,Z…
阅读更多...
算法14-求最长子序列

算法14-求最长子序列

题目&#xff1a; 给定数组arr。求最长的有序子序列的长度&#xff0c;返回长度int 分析&#xff1a; 1 要求的子串是有序的&#xff0c;就要比大小 2 用最暴力大方法&#xff0c;看成窗口问题&#xff0c;每一个元素求出它左边的最长序列子串&#xff0c;写入一个数组dp&…
阅读更多...
最长子序列——动态规划

最长子序列——动态规划

动态规划算法通常用于求解具有某种最优性质的问题。动态规划算法与分治法类似&#xff0c;其基本思想也是将待求解问题分解成若干个子问题&#xff0c;先求解子问题&#xff0c;然后从这些子问题的解得到原问题的解。与分治法不同的是&#xff0c;适合于用动态规划求解的问题&a…
阅读更多...
最长公共子串与最长子序列

最长公共子串与最长子序列

一 序 本文属于《图解算法》系列&#xff0c;上一篇整理了动态规划&#xff0c;动态规划可以帮助我们解决给定约束条件下找到最优解&#xff0c;例如背包问题。 在问题可分解为彼此独立且离散的子问题时&#xff0c;就可使用动态规划来解决。 在看个例子&#xff0c;求两个字…
阅读更多...
动态规划：最长子序列

动态规划：最长子序列

最长公共子序列&#xff1a; 链接&#xff1a;https://www.nowcoder.com/questionTerminal/9ae56e5bdf4f480387df781671db5172 题目&#xff1a; 我们有两个字符串m和n&#xff0c;如果它们的子串a和b内容相同&#xff0c;则称a和b是m和n的公共子序列。子串中的字符不一定在原字…
阅读更多...
C++最长子序列

C++最长子序列

LeedCode-300. 最长上升子序列 LeetCode-300. 最长上升子序列 方法一&#xff1a;O(n^2)可能会超时&#xff1b;方法二&#xff1a;贪心二分法&#xff0c;使用lower_bound()&#xff1b; 下面是贪心二分算法&#xff1a; 由于要得到最长的递增子序列&#xff0c;就要让序列…
阅读更多...
数组：最长子序列问题四种解法

数组：最长子序列问题四种解法

数组&#xff1a;最长子序列问题四种解法 问题描述&#xff1a; 给定一个整数数组 nums &#xff0c;找到一个具有最大和的连续子数组&#xff08;子数组最少包含一个元素&#xff09;&#xff0c;返回其最大和。 示例 1 : 输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子…
阅读更多...
动态规划：最长子序列问题

动态规划：最长子序列问题

关于动态规划中的最长子序列问题有很多优秀的解读&#xff0c;在这里推荐一位博主的关于最长子序列的文章&#xff0c;非常不错&#xff0c;配有大量的图片和文字解答&#xff0c;在这里推荐给大家。本文章转载自这里 1.基本概念 首先需要科普一下&#xff0c;最长公共子序列…
阅读更多...
一道有趣的最长子序列问题

一道有趣的最长子序列问题

一道有趣的最长子序列问题 – 潘登同学的金融经济学笔记 文章目录 一道有趣的最长子序列问题 -- 潘登同学的金融经济学笔记 来源求解递推公式算法实现 来源 前几天在刷视频的时候&#xff0c;发现了这样一道题 所谓子序列就是一个序列 a i 1 , a i 2 , ⋯ , a i n a_{i1},a_{…
阅读更多...
最长子序列最长子串的题型汇总

最长子序列最长子串的题型汇总

1.最长公共子序列的长度 题目&#xff1a;对于两个字符串&#xff0c;请设计一个高效算法&#xff0c;求他们的最长公共子序列的长度&#xff0c;这里的最长公共子序列定义为有两个序列U1,U2,U3...Un和V1,V2,V3...Vn,其中Ui&ltUi1&#xff0c;Vi&ltVi1。且A[Ui] B[Vi…
阅读更多...
动态规划解最长子序列问题

动态规划解最长子序列问题

动态规划法 经常会遇到复杂问题不能简单地分解成几个子问题&#xff0c;而会分解出一系列的子问题。简单地采用把大问题分解成子问题&#xff0c;并综合子问题的解导出大问题的解的方法&#xff0c;问题求解耗时会按问题规模呈幂级数增加。 为了节约重复求相同子问题的时间&…
阅读更多...
推荐文章

Copyright @ 2022~2023