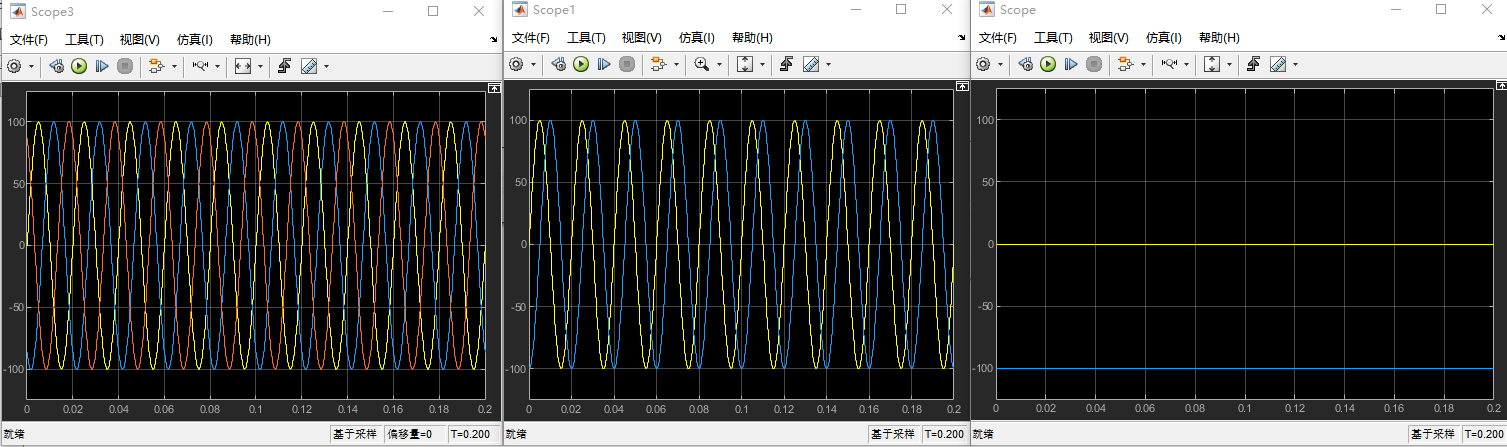
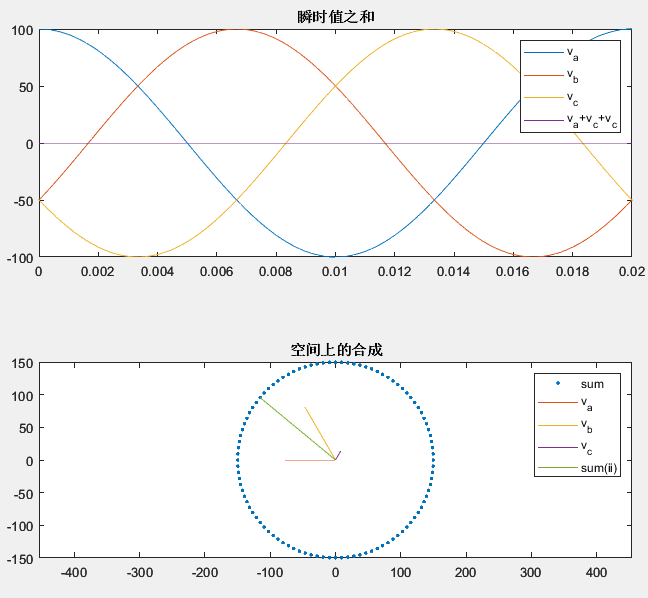
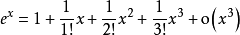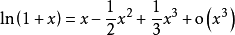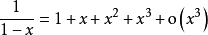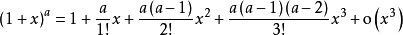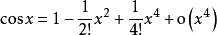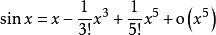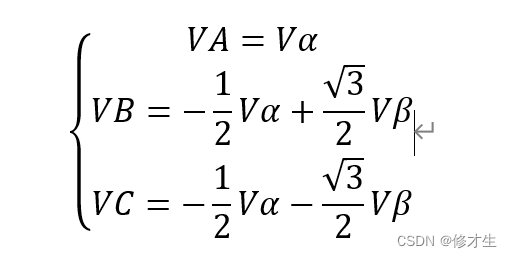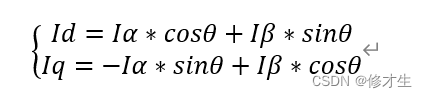Taylor’s Formula - 泰勒公式

泰勒公式应用于数学、物理领域，是一个用函数在某点的信息描述其附近取值的公式。如果函数足够平滑的话，在已知函数在某一点的各阶导数值的情况之下，泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值。泰勒公式还给出了这个多项式和实际的函数值之间的偏差。

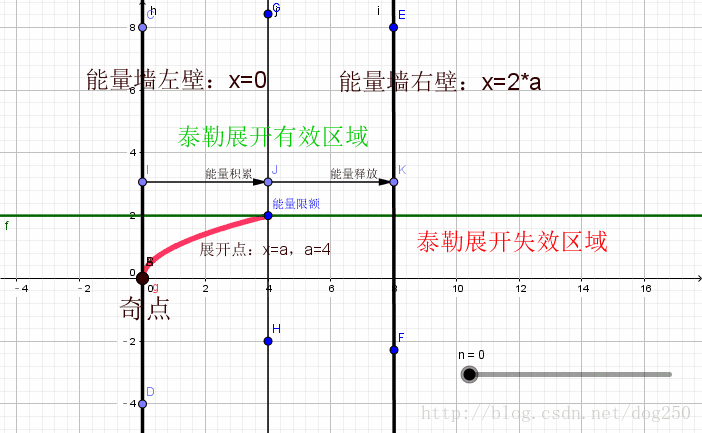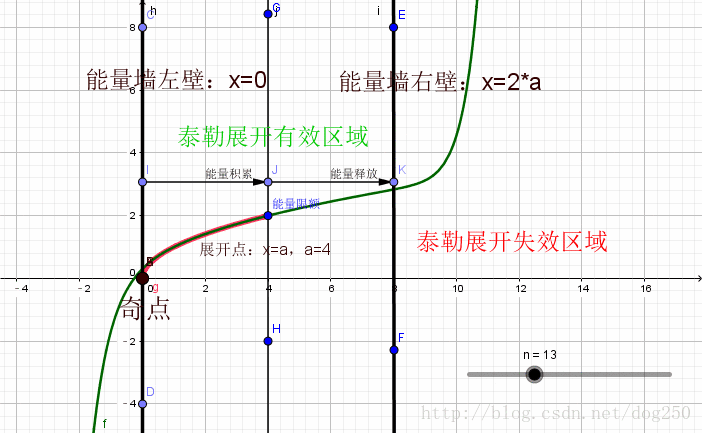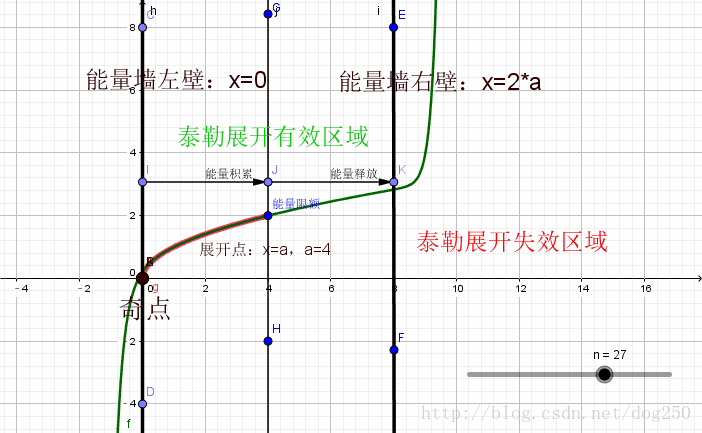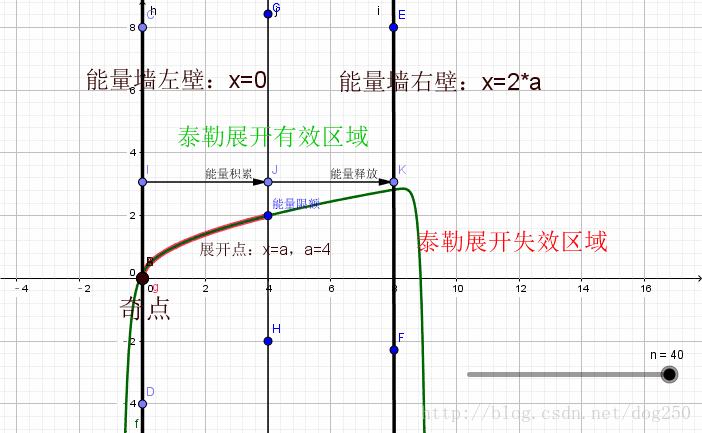
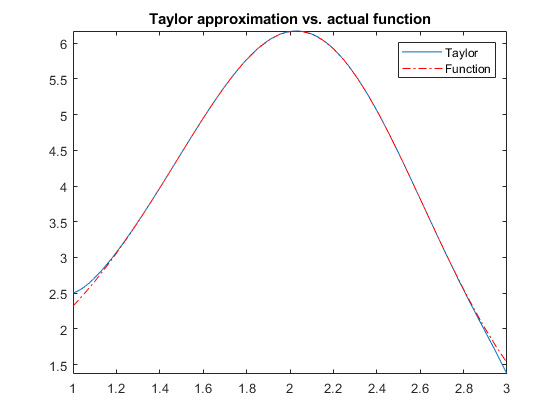
泰勒公式是将一个在 $x=x_0$ 处具有 $n$ 阶导数的函数 $f(x)$ 利用关于 $(x-x_0)$ 的 $n$ 次多项式来逼近函数的方法。

若函数 $f(x)$ 在包含 $x_0$ 的某个闭区间 $[a,b]$ 上具有 $n$ 阶导数，且在开区间 $(a,b)$ 上具有 $(n+1)$ 阶导数，则对闭区间 $[a,b]$ 上任意一点 $x$，成立下式：

其中，$f^{(n)}(x_0)$ 表示 $f(x)$ 的 $n$ 阶导数，等号后的多项式称为函数 $f(x)$ 在 $x_0$ 处的泰勒展开式，剩余的 $R_n(x)$ 是泰勒公式的余项，是 $(x-x_0{)}^n$ 的高阶无穷小。

The Lagrange form of the remainder term states that there exists a number $c$ between $a$ and $x$ such that
剩余项的拉格朗日形式表示在 $a$ 和 $x$ 之间存在数字 $c$，使得

The Cauchy form of the remainder term states that there exists a number c between a and x such that
剩余项的柯西形式表示在 $a$ 和 $x$ 之间存在数字 $c$，使得

The integral form of the remainder term is
剩余项的整数形式是

1. 常用函数的泰勒公式