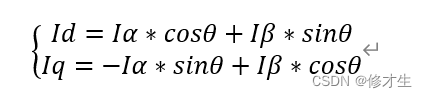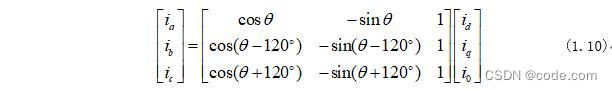BLDC矢量控制坐标变换
本文的目的在于梳理三相电机旋转矢量以及Clarke变换和Park变换的知识并给出推导。
文章目录
- BLDC矢量控制坐标变换
- 前言
- 一、从旋转矢量说起
- 二、Clarke变换
- 三、一般实际使用的Clarke变换
- 四、Clarke变换的性质
- 五、Park变换
- 六、Park变换的性质
- 七、功率的变换
- 总结
前言
最近想入手无刷电机的矢量控制,发现资料上比较零散,对一些变换公式说的不够清楚,让人倍感苦恼,为了夯实基础,扫除学习上的拦路虎,这里决心静下心来认真推导坐标变换公式。
一、从旋转矢量说起
三个线圈在空间(电角度空间)成120°放置,并且电流的相位也相差120°。
电流产生同相位的磁动势, A B C ABC ABC三相的磁动势分别 F c o s ( ω t ) , F c o s ( ω t − 2 π 3 ) , F c o s ( ω t + 2 π 3 ) Fcos({\omega}t),Fcos({\omega}t-\frac{2\pi}{3}),Fcos({\omega}t+\frac{2\pi}{3}) Fcos(ωt),Fcos(ωt−32π),Fcos(ωt+32π)。
为了书写方便,我们令相位 φ = ω t {\varphi=\omega}t φ=ωt。
三个磁动势为:
{ F a = F c o s φ F b = F c o s ( φ − 2 π 3 ) F c = F c o s ( φ + 2 π 3 ) … … 1 \left\{\begin{aligned} &F_a=Fcos\varphi\\ &F_b=Fcos(\varphi-\frac{2\pi}{3})\\ &F_c=Fcos(\varphi+\frac{2\pi}{3})\end{aligned}\right.……1 ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧Fa=FcosφFb=Fcos(φ−32π)Fc=Fcos(φ+32π)……1
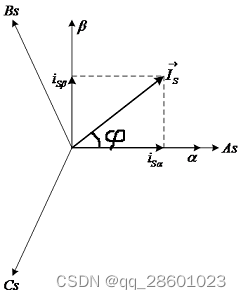
为了表示这三个量的空间关系,也为了方便计算,我们在复平面上处理空间位置关系:
设 α \alpha α轴对应复平面的实轴, β \beta β轴对应复平面的虚轴,则这三相磁动势可表示如下:
A相的矢量: F c o s φ = F 2 ( e j φ + e − j φ ) Fcos\varphi=\frac{F}{2}(e^{j\varphi}+e^{-j\varphi}) Fcosφ=2F(ejφ+e−jφ)
B相的矢量: F c o s ( φ − 2 π 3 ) e j 2 π 3 = F 2 ( e j ( φ − 2 π 3 ) + e − j ( φ − 2 π 3 ) ) e j 2 π 3 Fcos(\varphi-\frac{2\pi}{3})e^{j\frac{2\pi}{3}}=\frac{F}{2}(e^{j(\varphi-\frac{2\pi}{3})}+e^{-j(\varphi-\frac{2\pi}{3})})e^{j\frac{2\pi}{3}} Fcos(φ−32π)ej32π=2F(ej(φ−32π)+e−j(φ−32π))ej32π
C相的矢量: F c o s ( φ + 2 π 3 ) e − j 2 π 3 = F 2 ( e j ( φ + 2 π 3 ) + e − j ( φ + 2 π 3 ) ) e − j 2 π 3 Fcos(\varphi+\frac{2\pi}{3})e^{-j\frac{2\pi}{3}}=\frac{F}{2}(e^{j(\varphi+\frac{2\pi}{3})}+e^{-j(\varphi+\frac{2\pi}{3})})e^{-j\frac{2\pi}{3}} Fcos(φ+32π)e−j32π=2F(ej(φ+32π)+e−j(φ+32π))e−j32π
三个矢量的总和为:
F 2 [ e j φ + e − j φ + ( e j ( φ − 2 π 3 ) + e − j ( φ − 2 π 3 ) ) e j 2 π 3 + ( e j ( φ + 2 π 3 ) + e − j ( φ + 2 π 3 ) ) e − j 2 π 3 ] \frac{F}{2}[e^{j\varphi}+e^{-j\varphi}+(e^{j(\varphi-\frac{2\pi}{3})}+e^{-j(\varphi-\frac{2\pi}{3})})e^{j\frac{2\pi}{3}}+(e^{j(\varphi+\frac{2\pi}{3})}+e^{-j(\varphi+\frac{2\pi}{3})})e^{-j\frac{2\pi}{3}}] 2F[ejφ+e−jφ+(ej(φ−32π)+e−j(φ−32π))ej32π+(ej(φ+32π)+e−j(φ+32π))e−j32π]
= F 2 ( e j φ + e − j φ + e j φ + e − j ( φ + 2 π 3 ) + e j φ + e − j ( φ − 2 π 3 ) ) =\frac{F}{2}(e^{j\varphi}+e^{-j\varphi}+e^{j\varphi}+e^{-j(\varphi+\frac{2\pi}{3})}+e^{j\varphi}+e^{-j(\varphi-\frac{2\pi}{3})}) =2F(ejφ+e−jφ+ejφ+e−j(φ+32π)+ejφ+e−j(φ−32π))
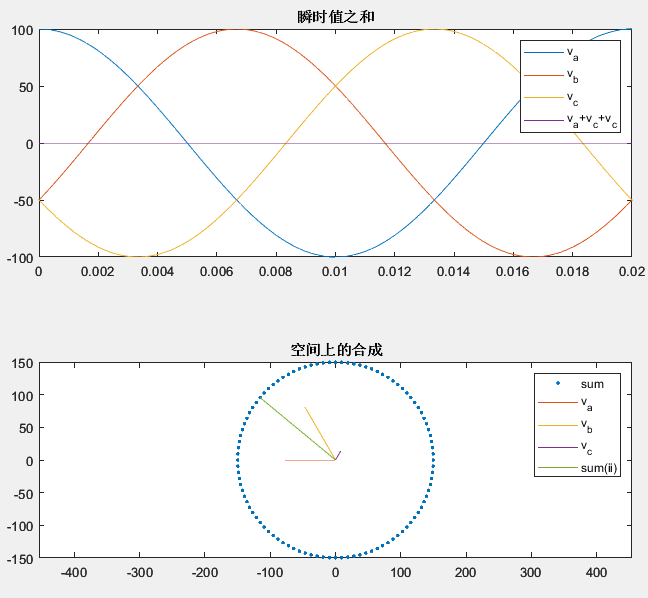
可以看到偶数项的旋转恰好抵消了,结果为 3 2 F e j φ = 3 2 F e j ω t \frac{3}{2}Fe^{j\varphi}=\frac{3}{2}Fe^{j{\omega}t} 23Fejφ=23Fejωt,于是我们得到大小为 3 2 F \frac{3}{2}F 23F的以角速度 ω \omega ω逆时针旋转的矢量 3 2 F e j ω t \frac{3}{2}Fe^{j{\omega}t} 23Fejωt。
抛开具体的旋转角速度,只看相位角 φ \varphi φ,对于像1式那种(三相幅值有120°相差且空间电角度相差120°的矢量),他们三个的矢量和就有一个重要的公式:
F c o s φ + F c o s ( φ − 2 π 3 ) e j 2 π 3 + F c o s ( φ + 2 π 3 ) e − j 2 π 3 = 3 2 F e j φ … … 2 Fcos\varphi+Fcos(\varphi-\frac{2\pi}{3})e^{j\frac{2\pi}{3}}+Fcos(\varphi+\frac{2\pi}{3})e^{-j\frac{2\pi}{3}}=\frac{3}{2}Fe^{j\varphi}……2 Fcosφ+Fcos(φ−32π)ej32π+Fcos(φ+32π)e−j32π=23Fejφ……2
这里特别提一下,永磁铁转子的磁场分解与合成容易给人造成误解,有人可能会认为“认为永磁体转子的磁场先分解到 A B C ABC ABC三个空间方向然后再按上述规则合成矢量,合成后应该是一个大小和永磁体转子原来磁场一样的以 ω \omega ω是磁场吧?”,但不幸的是并不是这样的:
假设永磁体转子的磁场强度为 ψ f ψ_f ψf且它与 A A A相的夹角为 θ \theta θ,则穿过 A A A相线圈的磁场为 ψ f c o s θ ψ_fcos\theta ψfcosθ,同理通过 B B B相线圈的磁场为 ψ f c o s ( θ − 2 π 3 ) ψ_fcos(\theta-\frac{2\pi}{3}) ψfcos(θ−32π),而通过 C C C相线圈的磁场为 ψ f c o s ( θ + 2 π 3 ) ψ_fcos(\theta+\frac{2\pi}{3}) ψfcos(θ+32π)。
因此从变换公式2式可以看出:
ψ f c o s θ + ψ f c o s ( θ − 2 π 3 ) e j 2 π 3 + ψ f c o s ( θ + 2 π 3 ) e − j 2 π 3 = 3 2 ψ f e j θ ψ_fcos\theta+ψ_fcos(\theta-\frac{2\pi}{3})e^{j\frac{2\pi}{3}}+ψ_fcos(\theta+\frac{2\pi}{3})e^{-j\frac{2\pi}{3}}=\frac{3}{2}ψ_fe^{j{\theta}} ψfcosθ+ψfcos(θ−32π)ej32π+ψfcos(θ+32π)e−j32π=23ψfejθ
因此需要注意上述矢量合成实际上是一种数学变换,永磁铁转子的磁场变换并不是变换成一个大小为 ψ f ψ_f ψf的旋转磁场,而是变换成一个大小为 3 2 ψ f \frac{3}{2}ψ_f 23ψf的旋转磁场。
二、Clarke变换
我们仍然用下图作说明:
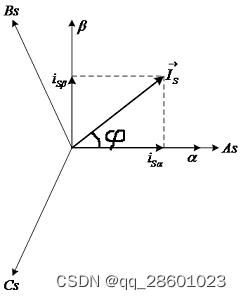
我们把第一节关于旋转矢量的特殊问题,过渡到具有一般价值的3相2相变换上。
先把公式1带入公式2(再次强调三相量一定是形如公式1的量):
F a + F b e j 2 π 3 + F c e − j 2 π 3 = 3 2 F e j φ … … 2 F_a+F_be^{j\frac{2\pi}{3}}+F_ce^{-j\frac{2\pi}{3}}=\frac{3}{2}Fe^{j\varphi}……2 Fa+Fbej32π+Fce−j32π=23Fejφ……2
表达成矩阵形式:
3 2 F [ c o s φ s i n φ ] = [ F α F β ] = [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] [ F a F b F c ] \frac{3}{2}F\begin{bmatrix}cos\varphi\\sin\varphi\end{bmatrix}=\begin{bmatrix}F_\alpha\\F_\beta\end{bmatrix}=\begin{bmatrix}1&-\frac{1}{2}&-\frac{1}{2}\\0&\frac{\sqrt3}{2}&-\frac{\sqrt3}{2}\end{bmatrix} \begin{bmatrix}F_a\\F_b\\F_c\end{bmatrix} 23F[cosφsinφ]=[FαFβ]=[10−2123−21−23]⎣⎡FaFbFc⎦⎤
我们不具体指定某一具体量,而是从数学上抽象的看待三相矢量 F a , F b , F c F_a,F_b,F_c Fa,Fb,Fc,经过上面的变换,可以合成一个大小为原来 3 2 \frac{3}{2} 23的电角度和 F a F_a Fa相同的矢量,这个矢量在 α β \alpha\beta αβ坐标下的分量记为 F α , F β F_\alpha,F_\beta Fα,Fβ。
通过变换 [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] \begin{bmatrix}1&-\frac{1}{2}&-\frac{1}{2}\\0&\frac{\sqrt3}{2}&-\frac{\sqrt3}{2}\end{bmatrix} [10−2123−21−23]把再 A B C ABC ABC坐标下的三相矢量 [ F a F b F c ] \begin{bmatrix}F_a\\F_b\\F_c\end{bmatrix} ⎣⎡FaFbFc⎦⎤变换成了 α β \alpha\beta αβ两相坐标下的矢量 [ F α F β ] \begin{bmatrix}F_\alpha\\F_\beta\end{bmatrix} [FαFβ]。
这个矩阵就是我们需要的Clarke变换了。
注意:如果 F a F_a Fa或 F b F_b Fb或 F c F_c Fc的大小为F,则 F α F_\alpha Fα或 F β F_\beta Fβ的大小就是 3 2 F \frac{3}{2}F 23F。
那么如何通过 α β \alpha\beta αβ坐标下的矢量还原三相 A B C ABC ABC下的各分量呢,由于:
[ F α F β ] = 3 2 F [ c o s φ s i n φ ] \begin{bmatrix}F_\alpha\\F_\beta\end{bmatrix} =\frac{3}{2}F\begin{bmatrix}cos\varphi\\sin\varphi\end{bmatrix} [FαFβ]=23F[cosφsinφ]
即: F α = 3 2 F c o s φ , F β = 3 2 F s i n φ F_\alpha=\frac{3}{2}Fcos\varphi,F_\beta=\frac{3}{2}Fsin\varphi Fα=23Fcosφ,Fβ=23Fsinφ
而在 A B C ABC ABC中又有: F a = F c o s φ , F b = F c o s ( φ − 2 π 3 ) , F c = F c o s ( φ + 2 π 3 ) F_a=Fcos\varphi,F_b=Fcos(\varphi-\frac{2\pi}{3}),F_c=Fcos(\varphi+\frac{2\pi}{3}) Fa=Fcosφ,Fb=Fcos(φ−32π),Fc=Fcos(φ+32π)。
利用简单的三角公式,我们能 F α , F β F_\alpha,F_\beta Fα,Fβ表示 F a , F b , F c F_a,F_b,F_c Fa,Fb,Fc,写成矩阵形式就有:
[ F a F b F c ] = 2 3 [ 1 0 − 1 2 3 2 − 1 2 − 3 2 ] [ F α F β ] = [ 2 3 0 − 1 3 3 3 − 1 3 − 3 3 ] [ F α F β ] \begin{bmatrix}F_a\\F_b\\F_c\end{bmatrix} =\frac{2}{3}\begin{bmatrix}1&0\\-\frac{1}{2}&\frac{\sqrt{3}}{2}\\-\frac{1}{2}&-\frac{\sqrt3}{2}\end{bmatrix} \begin{bmatrix}F_\alpha\\F_\beta\end{bmatrix} =\begin{bmatrix}\frac{2}{3}&0\\-\frac{1}{3}&\frac{\sqrt{3}}{3}\\-\frac{1}{3}&-\frac{\sqrt3}{3}\end{bmatrix} \begin{bmatrix}F_\alpha\\F_\beta\end{bmatrix} ⎣⎡FaFbFc⎦⎤=32⎣⎢⎡1−21−21023−23⎦⎥⎤[FαFβ]=⎣⎢⎡32−31−31033−33⎦⎥⎤[FαFβ]
这样我们就得到了Clarke反变换。
三、一般实际使用的Clarke变换
上一节中得到了特殊的Clarke变换,正变换后分量的振幅是原来分量的 3 2 \frac{3}{2} 23,但实际应用中为了适应各种需求,常常在变换中增加系数 K K K(例如令 K = 2 3 K=\frac{2}{3} K=32以保证数学变换后振幅相同),这构成实际的Clarke变换:
Clarke变换:
[ F α F β ] = K [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] [ F a F b F c ] \begin{bmatrix}F_\alpha\\F_\beta\end{bmatrix} =K\begin{bmatrix}1&-\frac{1}{2}&-\frac{1}{2}\\0&\frac{\sqrt3}{2}&-\frac{\sqrt3}{2}\end{bmatrix} \begin{bmatrix}F_a\\F_b\\F_c\end{bmatrix} [FαFβ]=K[10−2123−21−23]⎣⎡FaFbFc⎦⎤
Clarke逆变换:
[ F a F b F c ] = 1 K [ 2 3 0 − 1 3 3 3 − 1 3 − 3 3 ] [ F α F β ] \begin{bmatrix}F_a\\F_b\\F_c\end{bmatrix} =\frac{1}{K}\begin{bmatrix}\frac{2}{3}&0\\-\frac{1}{3}&\frac{\sqrt{3}}{3}\\-\frac{1}{3}&-\frac{\sqrt3}{3}\end{bmatrix} \begin{bmatrix}F_\alpha\\F_\beta\end{bmatrix} ⎣⎡FaFbFc⎦⎤=K1⎣⎢⎡32−31−31033−33⎦⎥⎤[FαFβ]
四、Clarke变换的性质
下面规定如下记号,从变换的观点来看Clarke变换的性质:
C = K [ 1 − 1 2 − 1 2 0 3 2 − 3 2 ] , C − 1 = 1 K [ 2 3 0 − 1 3 3 3 − 1 3 − 3 3 ] \bm{C}=K\begin{bmatrix}1&-\frac{1}{2}&-\frac{1}{2}\\0&\frac{\sqrt3}{2}&-\frac{\sqrt3}{2}\end{bmatrix}, \bm{C^{-1}}=\frac{1}{K}\begin{bmatrix}\frac{2}{3}&0\\-\frac{1}{3}&\frac{\sqrt{3}}{3}\\-\frac{1}{3}&-\frac{\sqrt3}{3}\end{bmatrix} C=K[10−2123−21−23],C−1=K1⎣⎢⎡32−31−31033−33⎦⎥⎤
注意: 时刻牢记,上述变换是在三相矢量(看公式1) [ F a F b F c ] \begin{bmatrix}F_a\\F_b\\F_c\end{bmatrix} ⎣⎡FaFbFc⎦⎤和 [ F α F β ] \begin{bmatrix}F_\alpha\\F_\beta\end{bmatrix} [FαFβ]的集合上进行的,它两都是 φ \varphi φ的函数,所以这两向量的实际自由度是一维的,所以存在变换,任意三维矢量和二维是矢量是不存在变换的,所以下面理解变换时不要直接去乘矩阵验证,这里的变换不具有全线性空间的可逆性,下面表述性质的时候不会写出被变换的向量了。
1.变换可逆: C C − 1 = E , C C − 1 = E \bm{C}\bm{C^{-1}}=\bm{E},\bm{C}\bm{C^{-1}}=\bm{E} CC−1=E,CC−1=E
其中 E \bm{E} E是变换的单位元,这两个 E \bm{E} E写法一样,但实际不同,它们作用的矢量空间也不一样,见注意,还有再强调:不要用直接矩阵相乘的观点来看待问题。
2.转置性质:
这个性质从矩阵上很容易看出来
C T = 3 K 2 2 C − 1 , C − 1 T = 2 3 K 2 C \bm{C^T}=\frac{3K^2}{2}\bm{C^{-1}},\bm{{C^{-1}}^T}=\frac{2}{3K^2}\bm{C} CT=23K2C−1,C−1T=3K22C
五、Park变换
如下图所示:
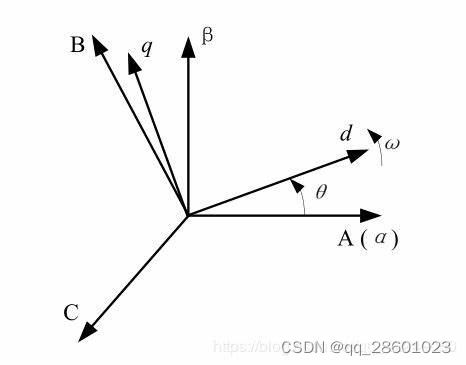
Park变换实际上就是代表了坐标的旋转,名为 d , q d,q d,q的坐标系,相对于 α , β \alpha,\beta α,β坐标系逆时针旋转了 θ \theta θ角度,则dq坐标系中的矢量变换关系为:
Park变换:
[ F d F q ] = [ c o s θ s i n θ − s i n θ c o s θ ] [ F α F β ] \begin{bmatrix}F_d\\F_q\end{bmatrix} =\begin{bmatrix}cos\theta&sin\theta\\-sin\theta&cos\theta\end{bmatrix} \begin{bmatrix}F_\alpha\\F_\beta\end{bmatrix} [FdFq]=[cosθ−sinθsinθcosθ][FαFβ]
Park逆变换
[ F α F β ] = [ c o s θ − s i n θ s i n θ c o s θ ] [ F d F q ] \begin{bmatrix}F_\alpha\\F_\beta \end{bmatrix} =\begin{bmatrix}cos\theta&-sin\theta\\sin\theta&cos\theta\end{bmatrix} \begin{bmatrix}F_d\\F_q\end{bmatrix} [FαFβ]=[cosθsinθ−sinθcosθ][FdFq]
六、Park变换的性质
下面规定如下记号,容易看出逆Park变换实际上就是把Park变换角度取负,从变换的观点来看Park变换的性质:
P ( θ ) = [ c o s θ s i n θ − s i n θ c o s θ ] , P ( − θ ) = [ c o s θ − s i n θ s i n θ c o s θ ] \bm{P(θ)}=\begin{bmatrix}cos\theta&sin\theta\\-sin\theta&cos\theta\end{bmatrix}, \bm{P(-θ)}=\begin{bmatrix}cos\theta&-sin\theta\\sin\theta&cos\theta\end{bmatrix} P(θ)=[cosθ−sinθsinθcosθ],P(−θ)=[cosθsinθ−sinθcosθ]
可加性: P ( θ 1 ) P ( θ 2 ) = P ( θ 1 + θ 2 ) \bm{P(θ_1)}\bm{P(θ_2)}=\bm{P(θ_1+\theta_2)} P(θ1)P(θ2)=P(θ1+θ2)
交换律: P ( θ 1 ) P ( θ 2 ) = P ( θ 2 ) P ( θ 1 ) \bm{P(θ_1)}\bm{P(θ_2)}=\bm{P(θ_2)}\bm{P(θ_1)} P(θ1)P(θ2)=P(θ2)P(θ1)
微分性质: d d t P ( θ ) = d θ d t P ( θ + π 2 ) , d d t P ( − θ ) = − d θ d t P ( − θ + π 2 ) \frac{d}{dt}\bm{P(θ)}=\frac{dθ}{dt}\bm{P(θ+\frac{\pi}{2})},\frac{d}{dt}\bm{P(-θ)}=-\frac{dθ}{dt}\bm{P(-θ+\frac{\pi}{2})} dtdP(θ)=dtdθP(θ+2π),dtdP(−θ)=−dtdθP(−θ+2π)
运算技巧:
关于矩阵对应的初等变换的意义:
[ 0 1 1 0 ] \begin{bmatrix}0&1\\1&0\end{bmatrix} [0110]
它左乘一个同尺寸的矩阵就是交换两行,而右乘同尺寸的矩阵就是交换两列。
有时候注意到这点可以简化计算。
对易性质:
利用 [ 0 1 1 0 ] \begin{bmatrix}0&1\\1&0\end{bmatrix} [0110]的初等变换的意义可以明显看出:
[ 0 1 1 0 ] P ( θ ) = P ( − θ ) [ 0 1 1 0 ] \begin{bmatrix}0&1\\1&0\end{bmatrix}\bm{P(θ)}=\bm{P(-θ)}\begin{bmatrix}0&1\\1&0\end{bmatrix} [0110]P(θ)=P(−θ)[0110]
P ( θ ) [ 0 1 1 0 ] = [ 0 1 1 0 ] P ( − θ ) \bm{P(θ)}\begin{bmatrix}0&1\\1&0\end{bmatrix}=\begin{bmatrix}0&1\\1&0\end{bmatrix}\bm{P(-θ)} P(θ)[0110]=[0110]P(−θ)
特殊角度变换: P ( π 2 ) = [ 0 1 − 1 0 ] , P ( − π 2 ) = [ 0 − 1 1 0 ] \bm{P(\frac{\pi}{2})}=\begin{bmatrix}0&1\\-1&0\end{bmatrix},\bm{P(-\frac{\pi}{2})}=\begin{bmatrix}0&-1\\1&0\end{bmatrix} P(2π)=[0−110],P(−2π)=[01−10]
七、功率的变换
首先注意到,Park变换并不影响变换前后的功率:
[ u d u q ] [ i d i q ] = [ u α u β ] P T ( θ ) P ( θ ) [ i α i β ] = [ u α u β ] [ i α i β ] \begin{bmatrix}u_d&u_q\end{bmatrix} \begin{bmatrix}i_d\\i_q\end{bmatrix} =\begin{bmatrix}u_\alpha&u_\beta\end{bmatrix} P^T(\theta)P(\theta) \begin{bmatrix}i_\alpha\\i_\beta\end{bmatrix} =\begin{bmatrix}u_\alpha&u_\beta\end{bmatrix} \begin{bmatrix}i_\alpha\\i_\beta\end{bmatrix} [uduq][idiq]=[uαuβ]PT(θ)P(θ)[iαiβ]=[uαuβ][iαiβ]
再考察Clarke变换,有:
[ u a u b u c ] [ i a i b i c ] = [ u α u β ] C − 1 T C − 1 [ i α i β ] \begin{bmatrix}u_a&u_b&u_c\end{bmatrix} \begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} =\begin{bmatrix}u_\alpha&u_\beta\end{bmatrix} {C^{-1}}^TC^{-1} \begin{bmatrix}i_\alpha\\i_\beta\end{bmatrix} [uaubuc]⎣⎡iaibic⎦⎤=[uαuβ]C−1TC−1[iαiβ]
利用Clarke变换的转置性质 C − 1 T = 3 K 2 2 C \bm{{C^{-1}}^T}=\frac{3K^2}{2}\bm{C} C−1T=23K2C:
[ u a u b u c ] [ i a i b i c ] = 2 3 K 2 [ u α u β ] [ i α i β ] \begin{bmatrix}u_a&u_b&u_c\end{bmatrix}\begin{bmatrix}i_a\\i_b\\i_c\end{bmatrix} =\frac{2}{3K^2} \begin{bmatrix}u_\alpha&u_\beta\end{bmatrix}\begin{bmatrix}i_\alpha\\i_\beta\end{bmatrix} [uaubuc]⎣⎡iaibic⎦⎤=3K22[uαuβ][iαiβ]
这里我们看出资料上一般声称Clarke变换中取 K = 2 3 K=\sqrt\frac{2}{3} K=32时可变换保持功率不变的原因。
总结
通过以上推导搞明白了刚开始接触这些知识的时候关于 K K K系数的不同取值的意义。