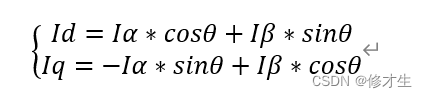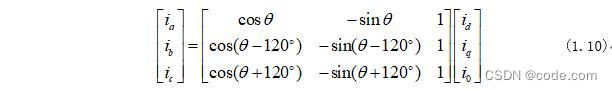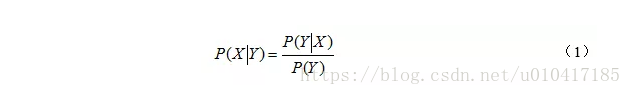简介

想用简单的办法把这些变换矩阵写出来，需要的时候可以使用，不用再去翻书（当然完全记住还是更快一些）。只是自己用来记忆这些变换的方法。

具体可以参考：手撕系列（2）：Clark变换与Park变换 - 知乎 (zhihu.com)
和这个视频：The Clarke and Park transformations (Episode 8)
还有这个（有空再看）：C. J. O’Rourke, M. M. Qasim, M. R. Overlin, and J. L. Kirtley, “A Geometric Interpretation of Reference Frames and Transformations: dq0, Clarke, and Park,” IEEE Trans. Energy Convers., vol. 34, no. 4, pp. 2070–2083, Dec. 2019, doi: 10.1109/TEC.2019.2941175.

Clarke变换

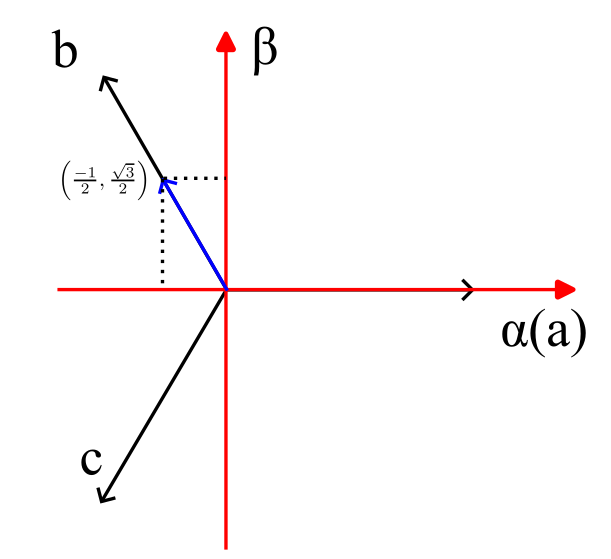
只看等幅值的Clarke变换。想一想abc三轴的方向上，单位长度的矢量，在αβ系中的坐标：

$\begin{align*} &a:(1,0) \\ &b:\left(\frac{-1}{2},\frac{\sqrt{3}}{2}\right) \\ &c:\left(\frac{-1}{2},-\frac{\sqrt{3}}{2}\right) \end{align*}$

把abc三个矢量的α坐标（实部）写第一行，β坐标（虚部）写第二行，乘上系数2/3，就是Clarke变换。
$\left[ \begin{matrix} x_\alpha \\ x_\beta \end{matrix} \right] =T_{3/2}\left[ \begin{matrix} x_a \\ x_b \\ x_c \end{matrix} \right]= \frac{2}{3} \left[ \begin{matrix} 1 & -\frac{1}{2} & -\frac{1}{2}\\ 0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \end{matrix} \right] \left[ \begin{matrix} x_a \\ x_b \\x_c \end{matrix} \right]$

去掉系数2/3，做个转置，就是Clarke反变换。因为正变换时采用了等幅值，乘以了系数2/3，所以反变换就不需要再加系数了——我大致是这样理解的。

$T_{2/3}= \left[\begin{matrix} 1 & 0 \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \\ -\frac{1}{2} & -\frac{\sqrt{3}}{2} \end{matrix}\right]$

Park变换

关于Park变换，一直记得主对角线上是cos，副对角线是是sin，总是记不清sin的负号在哪里。
矢量在逆时针旋转，角度增大，而经过park变换后成为一个直流量，所以，park变换的作用相当于对矢量做了顺时针的旋转，也就是 $e^{-j \theta}=cos \theta-jsin \theta$ 。把实部写第一行，虚部写第二行，得到了半个park变换矩阵，就知道了负号是在第一列的sin。。。
Park反变换， $e^{j \theta}=cos \theta+jsin \theta$ ，同理。

$\begin{align*} T_{r}(-\theta_r) &= \left[\begin{matrix} cos\theta_r & sin\theta_r \\ -sin\theta_r & cos\theta_r \\ \end{matrix} \right], \;(\text{Park}) \\ T_{r}(\theta_r) &= \left[\begin{matrix} cos\theta_r & -sin\theta_r \\ sin\theta_r & cos\theta_r \end{matrix} \right], \;(\text{inverse\,Park}) \\ \end{align*}$

具体也可以参考：手撕系列（2）：Clark变换与Park变换 - 知乎 (zhihu.com)

附1

在αβ系中， $\vec{x}=k_{\alpha}\vec{e}_{\alpha}+k_{\beta}\vec{e}_{\beta}$
在abc系中，同一个物理量， $\vec{x}=k_{a}\vec{e}_{a}+k_{b}\vec{e}_{b}+k_{c}\vec{e}_{c}$
其中 $\vec{e}_{x}$ 为坐标轴方向上的单位向量。
为了在两个坐标系中切换，需要找到单位向量之间的对应关系。
比如abc系->αβ系： $\vec{e}_{b}=-\frac{1}{2}\vec{e}_{\alpha}+ \frac{\sqrt{3}}{2}\vec{e}_{\beta}$
但是反过来，αβ系->abc系，其实挺难理解的，因为表示方法不唯一。。暂时还没懂。
比如 $\vec{e}_{\alpha}=\vec{e}_{a}=-\vec{e}_{b}-\vec{e}_{c}$

而系数2/3只是为了使变换后矢量的模和三相物理量的幅值相等。

附2

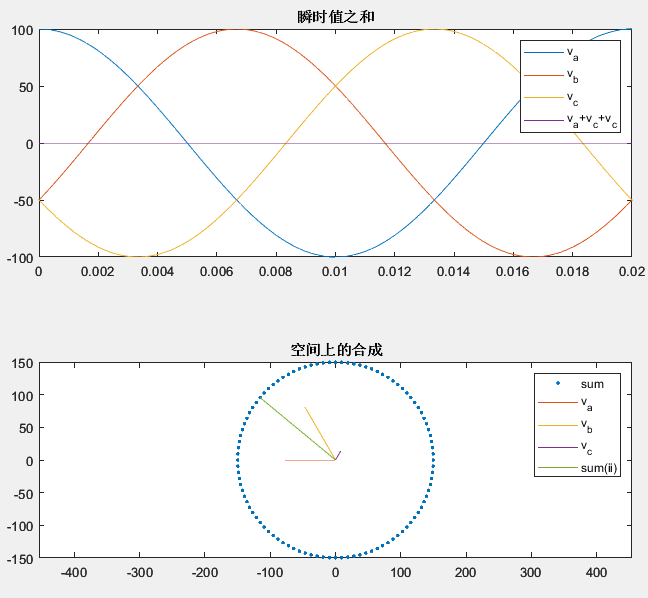
关于“为什么三相电压之和为0，却能合成一个旋转矢量”这个问题，用MATLAB简单画个图。代码注释里有大致的解释。

close
t = 0:0.2*1e-3:0.02;
f = 50;% 三相电压，正序
va = 100*cos(2*pi*f*t);
vb = 100*cos(2*pi*f*t - 2*pi/3);
vc = 100*cos(2*pi*f*t + 2*pi/3);% 三相电压被放置在空间上的不同位置
% 空间上的位置，令a相为0°
% b相超前a相120°，即位于2*pi/3
% c相滞后a相120°，即位于-2*pi/3
% 也就是说这三个矢量的方向不变，幅值随时间变化（幅值可以为负值）
% 后缀_c表示是矢量（复数），实部为在α轴上的投影，虚部为β轴上的投影
va_c = va;
vb_c = vb*cos(2*pi/3) + 1i*vb*sin(2*pi/3);
vc_c = vc*cos(-2*pi/3) + 1i*vc*sin(-2*pi/3);v_sum = va_c + vb_c + vc_c; % 三个矢量的合成结果subplot(2,1,1)
plot(t,va,t,vb,t,vc,t,va+vb+vc);
legend('v_a','v_b','v_c','v_a+v_c+v_c'); 
%可以看到在时间上，三相电压之和是0subplot(2,1,2)
plot(real(v_sum),imag(v_sum),'.');
axis equal
hold on
% 三相电压在空间上错开120°，合成结果落在一个圆上，且半径为1.5倍的相电压幅值
% 这里画了某个时刻的三个矢量的合成结果
ii = 40;
plot([0,real(va_c(ii))],[0,imag(va_c(ii))]);
plot([0,real(vb_c(ii))],[0,imag(vb_c(ii))]);
plot([0,real(vc_c(ii))],[0,imag(vc_c(ii))]);
plot([0,real(v_sum(ii))],[0,imag(v_sum(ii))]);
legend('sum','v_a','v_b','v_c','sum(ii)');