目录
- 写在前面
- 原理
- 代码
- CMakeLists.txt
- euler.cpp
- midpoint.cpp
- rk4.cpp
- compile&run
- 参考
- 完
写在前面
1、本文内容
数值积分方法:欧拉积分(Euler method)、中点积分(Midpoint method)和龙格-库塔法积分(Runge–Kutta methods)
2、转载请注明出处:
https://blog.csdn.net/qq_41102371/article/details/123351399
原理
欧拉积分、中点积分与龙格-库塔积分http://www.liuxiao.org/2018/05/%e6%ac%a7%e6%8b%89%e7%a7%af%e5%88%86%e3%80%81%e4%b8%ad%e7%82%b9%e7%a7%af%e5%88%86%e4%b8%8e%e9%be%99%e6%a0%bc%ef%bc%8d%e5%ba%93%e5%a1%94%e7%a7%af%e5%88%86/
数值积分方法(1)——龙格库塔积分https://zhuanlan.zhihu.com/p/536391602
VIO中的IMU数值积分与IMU预积分 https://zhuanlan.zhihu.com/p/107032156
代码
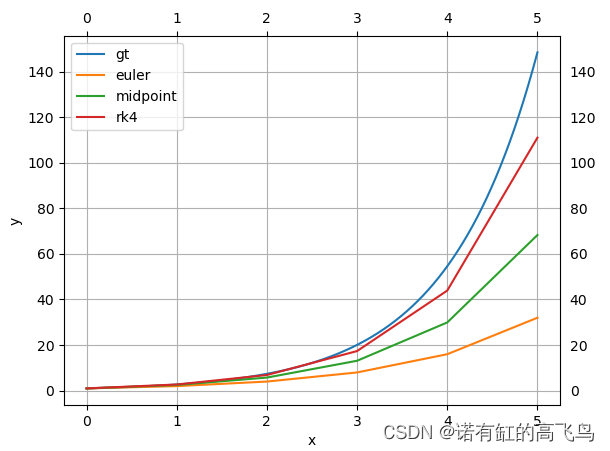
实现对 y = e x y=e^x y=ex的积分, y ( 0 ) = e ( 0 ) = 1 , y ′ ( 0 ) = e ( 0 ) = 1 y(0)=e^{(0)}=1, y'(0)=e^{(0)}=1 y(0)=e(0)=1,y′(0)=e(0)=1
CMakeLists.txt
cmake_minimum_required(VERSION 3.10)
project(Cmake_rk4)add_executable(rk4 rk4.cpp)
add_executable(midpoint midpoint.cpp)
add_executable(euler euler.cpp)
euler.cpp
// euler method
#include <iostream>
#include <cmath>
#include <fstream>
int main(int argc, char* argv[]){double e=2.7182818284;double n,error,y0,k0,k1,kn,yn,step;y0=atof(argv[1]);k1=k0=atof(argv[2]);step=atof(argv[3]);n=atoi(argv[4]);std::ofstream fout;fout.open("./data_euler.txt");if(!fout.is_open()){std::cout<<"open file failed!"<<std::endl;}fout<<0<<" "<<y0<<" "<<y0<<std::endl;for(int i=0;i<n;++i){kn=y0+step*k1;yn=y0+step*k1;double gt=std::pow(e,(i+1)*step);error=std::fabs(gt-yn);std::cout<<(i+1)*step<<std::endl;std::cout<<"y0: "<<y0<<" k0: "<<k0<<std::endl;std::cout<<"yn: "<<yn<<" kn: "<<kn<<std::endl<<"gt: "<<gt<<" error: "<<error<<std::endl;y0=yn;k1=k0=kn;std::cout<<"\n\n\n\n";fout<<(i+1)*step<<" "<<gt<<" "<<yn<<std::endl;}fout.close();return 0;
}
midpoint.cpp
// midpoint method
#include <iostream>
#include <cmath>
#include <fstream>int main(int argc, char* argv[]){double e=2.7182818284;double n,error,y0,k0,k1,k2,kn,yn,step;y0=atof(argv[1]);k1=k0=atof(argv[2]);step=atof(argv[3]);n=atoi(argv[4]);std::ofstream fout;fout.open("./data_midpoint.txt");if(!fout.is_open()){std::cout<<"open file failed!"<<std::endl;}fout<<0<<" "<<y0<<" "<<y0<<std::endl;for(int i=0;i<n;++i){kn=k2=y0+0.5*step*k1;yn=y0+step*kn;double gt=std::pow(e,(i+1)*step);error=std::fabs(gt-yn);std::cout<<(i+1)*step<<std::endl;std::cout<<"y0: "<<y0<<" k0: "<<k0<<std::endl;std::cout<<"k1: "<<k1<<" k2: "<<k2<<std::endl;std::cout<<"yn: "<<yn<<" kn: "<<kn<<std::endl<<"gt: "<<gt<<" error: "<<error<<std::endl;y0=yn;k1=k0=kn;std::cout<<"\n\n\n\n";fout<<(i+1)*step<<" "<<gt<<" "<<yn<<std::endl;}fout.close();return 0;
}
rk4.cpp
//runge kutta method
#include <iostream>
#include <cmath>
#include <fstream>
int main(int argc, char* argv[]){double e=2.7182818284;double n,error,y0,k0,k1,k2,k3,k4,kn,yn,step;y0=atof(argv[1]);k1=k0=atof(argv[2]);step=atof(argv[3]);n=atoi(argv[4]);std::ofstream fout;fout.open("./data_rk4.txt");if(!fout.is_open()){std::cout<<"open file failed!"<<std::endl;}fout<<0<<" "<<y0<<" "<<y0<<std::endl;for(int i=0;i<n;++i){k2=y0+0.5*step*k1;k3=y0+0.5*step*k2;k4=y0+step*k3;kn=(k1+2*k2+2*k3+k4)/6.0;yn=y0+step*kn;double gt=std::pow(e,(i+1)*step);error=std::fabs(gt-yn);std::cout<<(i+1)*step<<std::endl;std::cout<<"y0: "<<y0<<" k0: "<<k0<<std::endl;std::cout<<"k1: "<<k1<<" k2: "<<k2<<" k3: "<<k3<<" k4: "<<k4<<std::endl;std::cout<<"yn: "<<yn<<" kn: "<<kn<<std::endl<<"gt: "<<gt<<" error: "<<error<<std::endl;y0=yn;k1=k0=kn;std::cout<<"\n\n\n\n";fout<<(i+1)*step<<" "<<gt<<" "<<yn<<std::endl;}return 0;
}
compile&run
cmake -S ./ -B ./build
cmake --build ./build --config Release --parallel 4
./build/euler 1.0 1.0 1 5
./build/midpoint 1.0 1.0 1 5
./build/rk4 1.0 1.0 1 5
曲线图 https://blog.csdn.net/qq_41102371/article/details/125933558
参考
文中已列出
完
如有错漏,敬请指正











![[转]勒贝格积分的框架与通俗理解](http://data.artofproblemsolving.com/images/latex/e/0/1/e0184adedf913b076626646d3f52c3b49c39ad6d.gif)


