数值计算笔记之数值积分（二）龙贝格算法

article/2025/10/1 21:54:44

龙贝格求积公式也称为逐次分半加速法。它是在梯形公式、辛普森公式和柯特斯公式之间的关系的基础上，构造出一种加速计算积分的方法。作为一种外推算法，它在不增加计算量的前提下提高了误差的精度。

在等距基点的情况下，用计算机计算积分值通常都采用把区间逐次分半的方法进行。这样，前一次分割得到的函数值在分半以后仍可被利用,且易于编程。

一、变步长的梯形法

求 $\int_{a}^{b}f(x)dx$

<1> 首先在 $[a,b]$ 上用梯形公式，得 $T_{1}$

<2>将 $[a,b]$ 二等分，步长 $h=\frac{b-a}{2}$ ，用复化梯形公式，得 $T_{2}$

<3>将 $[a,b]$ 四等分，步长 $h=\frac{b-a}{4}$ ，用复化梯形公式，得 $T_{4}$

$\cdots \cdots$

<n>将将 $[a,b]$ 2n 等分，步长 $h=\frac{b-a}{2n}$ ，用复化梯形公式，得 $T_{2n}$

问题：

每一步是否能用到上一步得计算结果？
区间划分到什么程度，才满足精度要求？

分析：

<1>、n等分，步长 $h=\frac{b-a}{n}$ ， $T_{n}=\frac{h}{2}[f(a)+f(b)+2\sum_{k=1}^{n-1}f(x_{k})]$

<2>、 2n 等分，步长 $h^{'}=\frac{h}{2}$ ，记 $[x_{k},x_{k+1}]$ 的中点(图中红线)为 $x_{k+\frac{1}{2}}$ 。

则积分节点为： $x_{0},x_{\frac{1}{2}},x_{1},x_{\frac{3}{2}},x_{2},\cdots ,x_{n-1},x_{n-\frac{1}{2}},x_{n}$ （分为原节点和新增节点）

$T_{2n} = \frac{h^{'}}{2}[f(a)+f(b)+2\sum_{k=1}^{n-1}f(x_{k}) + 2\sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}})]$

$=\frac{1}{2}T_{n}+\frac{h}{2}\cdot \sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}})$ (注意：此 $h$ 是计算 $T_{n}$ 时的)

算法总结：

计算 $T_{n}=\frac{h}{2}[f(a)+f(b)+2\sum_{k=1}^{n-1}f(x_{k})]$
由递推公式 $T_{2n}=\frac{1}{2}T_{n}+\frac{h}{2}\cdot \sum_{k=0}^{n-1}f(x_{k+\frac{1}{2}})$
判断 $|T_{n} - T_{2n}| < \varepsilon$ （ $\varepsilon$ 为误差限），成立则返回 $T_{2n}$ 并输出。

变步长的梯形法代码（C++)：


//变步长梯形积分
double T2n(double(*f)(double), double a, double b, double error) {int n = 1;   double h = (b - a) / n;double Tn = (f(a) + f(b)) * h / 2.0;  //计算 n=1 时的积分，粗略值double T2n;     //步长变为一半后的积分值bool key = false;do {    //至少循环一次double Hn = 0.0;for (int k = 0; k < n; k++) {double x = a + (k + 0.5) * h;Hn += h * f(x);}T2n = (Tn + Hn) / 2.0;//判断误差if (fabs(Tn - T2n) < error) {key = true;}else {Tn = T2n;n *= 2;h /= 2;}} while (!key);return T2n;
}

二、龙贝格算法

$I - T_{2n} \approx \frac{1}{3}(T_{2n}-T_{n})$

$I$ 准确值
$T_{2n}$ 数值计算近似值
$\frac{1}{3}(T_{2n}-T_{n})$ 为误差

1、 $I \approx T_{2n}+ \frac{1}{3}(T_{2n}-T_{n})$ 记为 $S_{n}$ .

$=S_{n}$ ( $simpson$ 序列)

还存在误差

2、求 $simpson$ 公式的余项，可得：

$\frac{I-S_{2n}}{I-S_{n}}\approx \frac{1}{16}\Rightarrow I-S_{2n}\approx \frac{1}{15}(S_{2n}-S_{n})$

$\therefore C_{n} = S_{2n}+\frac{1}{15}(S_{2n}-S_{n})$ （柯特斯序列）

还存在误差

3、求柯特斯公式的余项，可得：

$R_{n}=C_{2n}+\frac{1}{63}\cdot (C_{2n}-C_{n})$ （龙贝格序列）

加权平均公式： $\frac{4T_{n}-T_{n}}{4-1} = S_{n}\cdots \frac{4^{2}S_{2n}-S_{n}}{4^{2}-1}=C_{n}\cdots \frac{4^{3}C_{2n}-C_{n}}{4^{3}-1}=R_{n}$

三、代码实现

$T_{n}=\frac{h}{2}[f(a)+f(b)+2\sum_{k=1}^{n-1}f(x_{k})]$
$S_{n}=T_{2n}+ \frac{1}{3}(T_{2n}-T_{n}) = \frac{4}{3}T_{2n}-\frac{1}{3}T_{n}$
$C_{n} = S_{2n}+\frac{1}{15}(S_{2n}-S_{n}) = \frac{16}{15}S_{2n}-\frac{1}{15}S_{n}$
$R_{n}=C_{2n}+\frac{1}{63}\cdot (C_{2n}-C_{n}) = \frac{64}{63}C_{2n}-\frac{1}{63}C_{n}$

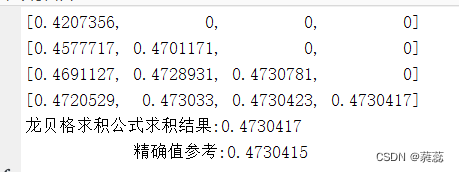
例： $f(x) = \int_{1}^{2}\frac{log(1+x^{2})}{1+x^{2}}$ ,程序结果为：

具体代码为(没有安装armadillo矩阵计算库的点这里)：

//#include<iostream>
//#include<armadillo>
//#include<iomanip>#include"romberg.h"using namespace std;
using namespace arma;int main()
{const double eps = 1e-6;int size = 50;Romberg.zeros(size, 4);Coefficient << 4 / 3.0 << 1 / 3.0 << endr<< 16 / 15.0 << 1 / 15.0 << endr<< 64 / 63.0 << 1 / 63.0 << endr;double a =1, b=2;cout << "请输入积分下限, a = ";cin >> a;cout  << "请输入积分上限, b = ";cin >> b;cout << endl;double result = getSn(a, b, eps);cout << "积分结果为：" << setprecision(8) << result << endl;
}

头文件为：

#pragma once
#include<iostream>
#include<math.h>
#include<armadillo>
#include<iomanip>
#include<vector>using namespace std;
using namespace arma;mat Romberg;                            //用于存放T、S、 C、R
mat Coefficient;                        //存放 计算系数
// 记录坐标值
vector<double> x_vec;
vector<double> y_vec;// 积分函数
double fun(double x) {double y = log(1 + pow(x, 2)) / (1 + pow(x, 2));return y;
}//存储对应坐标
void GreatXY(double a, double b, int n) {x_vec.clear();y_vec.clear();double h = (b - a) / n;for (int k = 0; k <= n; k++) {double x = a + h * k;double y = fun(x);x_vec.push_back(x);y_vec.push_back(y);}
}/*变步梯形积分a:积分下限b:积分上限n:节点数*/
double getTn(double a, double b, int n)
{GreatXY(a, b, n);double h = (b - a) / n;double Tn = h / 2.0 * (fun(a) + fun(b));for (int k = 1; k < n; k++) {double x = a + k * h;Tn += h * fun(x);}return Tn;
}void FillMatrix(double &a, double &b) {//填充Tnfor (int k = 0; k <= 4; k++) { //先计算k =0,1,2,3,4的情况，即将S1、S2计算出来，在|S1-S2|不符合误差情况时在更新矩阵。Romberg(k, 0) = getTn(a, b, pow(2, k));}//填充Sn(i=1)、Cn(i=2)、Rn(i=3)       //编程思想的行列，从零开始for (int i = 1; i <= 3; i++) {       //列for (int j = i; j <= 4; j++) {    //行Romberg(j, i) = Romberg(j, i - 1)*Coefficient(i - 1, 0) - Romberg(j - 1, i - 1)*Coefficient(i - 1, 1);}}
}double getSn(double a, double b,double eps){FillMatrix(a, b);//判断误差if (fabs(Romberg(4, 3) - Romberg(3, 3)) < eps) {return Romberg(4, 3);}else {for (int k = 5;; k++) {Romberg(k, 0) = getTn(a, b, pow(2, k));     //TRomberg(k, 1) = 4 / 3.0 *Romberg(k, 0) - 1 / 3.0*Romberg(k - 1, 0);           //SRomberg(k, 2) = 16 / 15.0*Romberg(k, 1) - 1 / 15.0*Romberg(k - 1, 1);      //CRomberg(k, 3) = 64 / 63.0 *Romberg(k, 2) - 1 / 63.0*Romberg(k - 1, 2);     //R//再次比较if (fabs(Romberg(k, 3) - Romberg(k-1, 3)) < eps) {return Romberg(k, 3);break;}if (k >= 50) {cout << "循环次数太多，请更换程序算法";return -1;break;}}}
}