实变函数自制笔记8：初识勒贝格积分

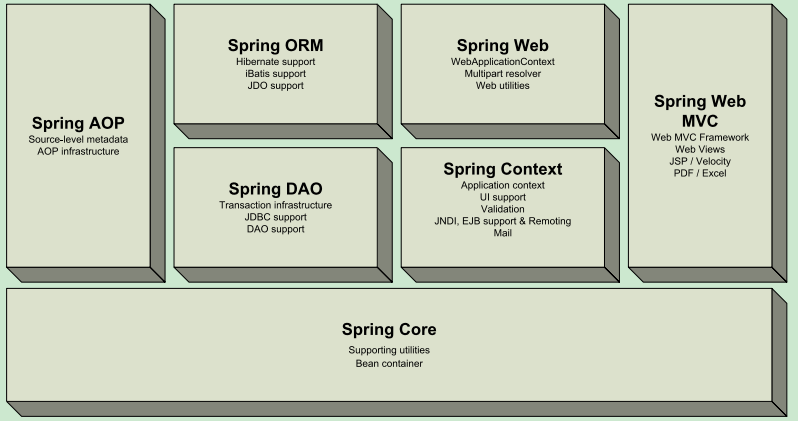
1、勒贝格（Lebesgue）积分：

背景：勒贝格积分是在勒贝格测度论的基础上建立起来的，这一理论可以统一处理函数有界、无界的情形，且函数也可以定义在更一般的点集（不一定是 $\left [ a,b \right ]$ ）上；特别的是它提供了比黎曼积分更加广泛有效的收敛定理；定义勒贝格积分的方法很多，这里先给出通过简单函数来定义的思路；
勒贝格积分的定义：

通过简单函数定义勒贝格积分：根据笔记6里的简单函数逼近定理，对于 $E$ 上任一非负可测函数 $f\left ( x \right )$ ，可以找到一列单调递增的简单函数 $\varphi _n\left ( x \right )$ ，使得 $\varphi _n\left ( x \right )\rightarrow f\left ( x \right )\left ( n\rightarrow \infty \right )$ ；而对于每个简单函数 $\varphi _n$ ，其在点集 $E_{i}^{\left ( n \right )}\left ( i=1,2,\cdots ,N_n \right )\left ( \bigcup_{i=1}^{N_n}E_{i}^{\left ( n \right )}=E \right )$ 上取值 $C_{i}^{\left ( n \right )}\left ( x\in E_{i} \right )$ （注：这里的 $\left ( n \right )$ 指的是，在 $i$ 值相同 $n$ 值不同 $\left (n_1\neq n_2 \right )$ 的情况下， $\varphi _{n_1},\varphi _{n_2}$ 各自对应的 $C_{i}^{\left ( n_1 \right )},C_{i}^{\left ( n_2 \right )}$ 之间并不相同），则有简单函数 $\varphi _n\left ( x \right )=\sum_{i=1}^{N_n}C_{i}^{\left ( n \right )} \chi _{E_{i}^{\left ( n \right )}}\left ( x \right )=C_{i}^{\left ( n \right )}\left ( x\in E_{i}^{\left ( n \right )} \right )$ ，其中 $\chi _{E_{i}^{\left ( n \right )}}\left ( x \right )=\left\{\begin{matrix} 1, & x\in E_{i}^{\left ( n \right )}\\ 0, & x\notin E_{i}^{\left ( n \right )} \end{matrix}\right.$ 指的是特征函数；由此便可得出简单函数 $\varphi _n$ 的积分为 $\sum_{i=1}^{N_n}C_{i}^{\left ( n \right )} m\left ( E_{i}^{\left ( n \right )} \right )$ ，若此和式极限存在，则可定义该极限为 $f\left ( x \right )$ 的积分；
通过分割值域定义勒贝格积分：已知在可测集 $E\subset \mathbb{R}^{n}$ 上有界可测函数 $f\left ( x \right )$ ，根据 $f\left ( x \right )$ 的值域随机的划分区域，区域的边界对应的 $f\left ( x_i \right )$ 值定义为 $l_i$ ，由此可以得出递增序列 $\left \{ l_i \right \}\left ( l_i< l_{i+1} \right )$ ，并令 $E_i=\left \{ x\in E\mid f\left ( x \right )\in \left ( l_i,l_{i+1} \right ] \right \}$ ，最后通过讨论和式 $\sum_{i}\xi _i m\left ( E_i \right ),\xi _i\in \left [ i_1,i_{i+1} \right ]$ 的极限是否存在来定义；之后勒贝格积分的定义就是这么来的；
通过对可测集作任意划分定义勒贝格积分：对 $E$ 作任意划分： $E=\bigcup_{i=1}^{m}E_i,E_i\cap E_j=\varnothing \left ( i\neq j \right )$ ；并令 $b_i=\inf_{x\in E_i}f\left ( x \right ),B_i=\sup_{x\in E_i}f\left ( x \right )$ ，然后像黎曼积分那样作对应于该划分的小和数 $\sum_{i=1}^{m}b_im\left ( E_i \right )$ 与大和数 $\sum_{i=1}^{m}B_im\left ( E_i \right )$ ，讨论相对于划分的加细，其大和数与小和数的极限是否相等；

有界可测函数的勒贝格积分/ $L$ -积分：已知 $f\left ( x \right )$ 为定义在有限测度 $\left (m\left ( E \right )< +\infty \right )$ 可测集 $E\subset \mathbb{R}^{n}$ 上的有界可测函数，不妨设 $f\left ( x \right )\in \left [ m,M \right ]$ ，并令 $D:l_0< m< l_1<l_2<\cdots <l_{n-1}<M<l_n$ 为 $f\left ( x \right )$ 值域的一个划分，且 $\delta \left ( D \right )=\max_{1\leqslant k\leqslant n}\left \{ l_k-l_{k-1} \right \}$ ， $E_k=\left \{ x\in E\mid f\left ( x \right )\in \left ( l_{k-1},l_k \right ] \right \}$ ； $\forall \xi _i\in \left [ l_{k-1},l_i \right ]$ ，有 $f\left ( x \right )$ 对应值域划分 $D$ 的一个和数 $S\left ( D \right )=\sum_{k=1}^{n}\xi _km\left ( E_k \right )$ ；若 $\lim_{\delta \left ( D \right )\rightarrow 0}S\left ( D \right )$ 存在且值为 $A$ ，则称有界可测函数 $f\left ( x \right )$ 在 $E$ 上是勒贝格可积的，并称 $A=\int _E f\left ( x \right )dx$ 为 $f\left ( x \right )$ 在 $E$ 上的勒贝格积分/ $L$ -积分；若 $E=\left [ a,b \right ]$ ，则记 $A=\int _{\left [ a,b \right ]} f\left ( x \right )dx$ ；
注意：

当 $f\left ( x \right )$ 为黎曼可积函数时，黎曼积分仍写作 $A=\int _{a}^{b} f\left ( x \right )dx$ ，写法与 $L$ -积分不同；不过之后我们会知道：当 $f\left ( x \right )$ 黎曼可积时， $\int _{\left [ a,b \right ]} f\left ( x \right )dx=\int _{a}^{b} f\left ( x \right )dx$ ；即勒贝格积分为黎曼积分的推广；
定义里的和数同黎曼积分一样也有大和数 $\overline{S}\left ( D \right )$ 与小和数 $\underline{S}\left ( D \right )$ ，显然有 $\underline{S}\left ( D \right )\leqslant S\left ( D \right ) \leqslant \overline{S}\left ( D \right )$ ，且： $\lim_{\delta \left ( D \right )\rightarrow 0}S\left ( D \right )$ 存在 $\Leftrightarrow$ $\lim_{\delta \left ( D \right )\rightarrow 0}\underline{S}\left ( D \right ),\lim_{\delta \left ( D \right )\rightarrow 0}\overline{S}\left ( D \right )$ 都存在且相等；
根据定义，很明显我们可以得到： $f\left ( x \right )$ 为定义在有限测度 $\left (m\left ( E \right )< +\infty \right )$ 可测集 $E\subset \mathbb{R}^{n}$ 上的有界可测函数 $\Rightarrow f\left ( x \right )$ 在 $E$ 上勒贝格可积（任一有界可测函数均是勒贝格可积的）；

非负可测函数的勒贝格积分/ $L$ -积分：已知 $f\left ( x \right )$ 为定义在有限测度 $\left (m\left ( E \right )< +\infty \right )$ 可测集 $E\subset \mathbb{R}^{n}$ 上的非负可测函数， $\forall m> 0$ ，若令 $\left \{ f\left ( x \right ) \right \}_m=\min\left \{ f\left ( x \right ),m \right \}$ ，则 $\left \{ f\left ( x \right ) \right \}_m$ 同样是定义在 $E$ 上的非负可测函数，而 $\left \{ f\left ( x \right ) \right \}_m\in \left [0,m \right ]$ 说明其有界，那么每个非负可测函数 $\left \{ f\left ( x \right ) \right \}_m$ 在 $E$ 上勒贝格可积；由于 $\int_{E}\left \{ f\left ( x \right ) \right \}_mdx$ 为单调数列，则 $\lim_{m\rightarrow \infty }\int_{E}\left \{ f\left ( x \right ) \right \}_mdx$ 总是存在的或者 $=+\infty$ ；那么我们称 $\int_{E}f\left ( x \right )dx=\lim_{m\rightarrow \infty }\int_{E}\left \{ f\left ( x \right ) \right \}_mdx$ 为非负可测函数 $f\left ( x \right )$ 在 $E$ 上的勒贝格积分/ $L$ -积分；若 $\int_{E}f\left ( x \right )dx< +\infty$ （为有限数），则非负可测函数 $f\left ( x \right )$ 在 $E$ 上是勒贝格可积的；
一般可测函数的勒贝格积分/ $L$ -积分：已知 $f\left ( x \right )$ 为定义在有限测度 $\left (m\left ( E \right )< +\infty \right )$ 可测集 $E\subset \mathbb{R}^{n}$ 上的可测函数，若 $\int_{E}f^+\left ( x \right )dx,\int_{E}f^-\left ( x \right )dx$ 至少有一个 $\neq +\infty$ ，则称 $\int_{E}f\left ( x \right )dx=\int_{E}f^+\left ( x \right )dx-\int_{E}f^-\left ( x \right )dx$ 为可测函数 $f\left ( x \right )$ 在 $E$ 上的勒贝格积分/ $L$ -积分；若 $\int_{E}f\left ( x \right )dx< +\infty$ （为有限数），则可测函数 $f\left ( x \right )$ 在 $E$ 上是勒贝格可积的；

2、可测函数勒贝格积分的性质与定理：

有界可测函数勒贝格积分的性质与定理：已知 $m\left ( E \right )<\infty$ ， $f\left ( x \right ),g\left ( x \right )$ 均为 $E$ 上的有界可测函数：

（线性性质1） $\forall c\in \mathbb{R}$ ， $\int_{E}cf\left ( x \right )dx=c\int_{E}f\left ( x \right )dx$ ；
（线性性质2） $\int_{E}\left (f\left ( x \right )+g\left ( x \right ) \right )dx=\int_{E}f\left ( x \right )dx+\int_{E}g\left ( x \right )dx$ ；
（可加性）若 $E_i$ 为 $E$ 的可测子集， $E_i\cap E_j=\varnothing \left ( i\neq j \right )$ ， $E=\bigcup_{i=1}^{m}E_i$ ；则： $\int_{E}f\left ( x \right )dx=\int_{E_1}f\left ( x \right )dx+\cdots +\int_{E_m}f\left ( x \right )dx$ ；
（保号性）当 $f\left ( x \right )\leqslant g\left ( x \right )$ 在 $E$ 上几乎处处成立（即 $f\left ( x \right )\leqslant g\left ( x \right ),\textup{a.e. }x\in E$ ）时，有 $\int_{E}f\left ( x \right )dx\leqslant \int_{E}g\left ( x \right )dx$ ；
已知 $f\left ( x \right )$ 为定义在有限测度 $\left (m\left ( E \right )< +\infty \right )$ 可测集 $E\subset \mathbb{R}^{n}$ 上的有界可测函数，若 $f\left ( x \right )\geqslant 0$ 在 $E$ 上几乎处处成立（即 $f\left ( x \right )\geqslant 0,\textup{a.e. }x\in E$ ），且 $\int_{E}f\left ( x \right )dx=0$ $\Rightarrow$ $f\left ( x \right )=0$ 在 $E$ 上几乎处处成立（即 $f\left ( x \right )= 0,\textup{a.e. }x\in E$ ）；

一般可测函数勒贝格积分的性质与定理：

已知 $f\left ( x \right )$ 在 $E$ 上可测，则： $f\left ( x \right )$ 在 $E$ 上勒贝格可积 $\Leftrightarrow$ $\left | f\left ( x \right ) \right |$ 在 $E$ 上勒贝格可积；
已知 $f\left ( x \right )$ 在 $E$ 上可测， $g\left ( x \right )$ 在 $E$ 上非负可积；当 $\left | f\left ( x \right ) \right |\leqslant g\left ( x \right )$ 在 $E$ 上几乎处处成立（即 $\left | f\left ( x \right ) \right |\leqslant g\left ( x \right ),\textup{a.e. }x\in E$ ）时，有 $f\left ( x \right )$ 在 $E$ 上可积，且有 $\int_{E}\left | f\left ( x \right ) \right |dx\leqslant \int_{E}g\left ( x \right )dx$ ；
（线性性质1） $\forall c\in \mathbb{R}$ ， $\int_{E}cf\left ( x \right )dx=c\int_{E}f\left ( x \right )dx$ ；
（线性性质2） $\int_{E}\left (f\left ( x \right )+g\left ( x \right ) \right )dx=\int_{E}f\left ( x \right )dx+\int_{E}g\left ( x \right )dx$ ；
（可加性）若 $E_i$ 为 $E$ 的可测子集， $E_i\cap E_j=\varnothing \left ( i\neq j \right )$ ， $E=\bigcup_{i=1}^{m}E_i$ ，则： $f\left ( x \right )$ 在 $E,E_i$ 上有积分，且有 $\int_{E}f\left ( x \right )dx=\int_{E_1}f\left ( x \right )dx+\cdots +\int_{E_m}f\left ( x \right )dx$ ；特别地，当 $f\left ( x \right )$ 在 $E$ 上非负可测时， $\int_{E}f\left ( x \right )dx\geqslant \int_{E_i}f\left ( x \right )dx,i=1,2,\cdots ,m$ ；
（保号性）当 $f\left ( x \right ),g\left ( x \right )$ 均在 $E$ 上有积分，且 $f\left ( x \right )\leqslant g\left ( x \right )$ 在 $E$ 上几乎处处成立（即 $f\left ( x \right )\leqslant g\left ( x \right ),\textup{a.e. }x\in E$ ）时，有 $\int_{E}f\left ( x \right )dx\leqslant \int_{E}g\left ( x \right )dx$ ；
当 $f\left ( x \right )$ 在 $E$ 上有积分，且 $f\left ( x \right )=g\left ( x \right )$ 在 $E$ 上几乎处处成立（即 $f\left ( x \right )= g\left ( x \right ),\textup{a.e. }x\in E$ ）时，有 $\int_{E}f\left ( x \right )dx=\int_{E}g\left ( x \right )dx$ ；

3、勒贝格积分与黎曼积分的关系：

背景：

前面有提到，勒贝格积分是黎曼积分的推广，他的类别也比黎曼积分类要多，即如果 $f\left ( x \right )$ 是黎曼可积的，那么 $f\left ( x \right )$ 一定也是勒贝格可积的；但反过来则不然：已知 $D\left ( x \right )=\left\{\begin{matrix} 1, & x\in \left [ 0,1 \right ]\cap \mathbb{Q}\\ 0, & x\in \left [ 0,1 \right ]\cap \left ( \mathbb{R}-\mathbb{Q} \right ) \end{matrix}\right.$ ，即 $D\left ( x \right )$ 所有在 $\left [ 0,1 \right ]$ 内的有理数对应值为1，在 $\left [ 0,1 \right ]$ 内的无理数对应值为0，则 $D\left ( x \right )$ 在 $\left [ 0,1 \right ]$ 上勒贝格可积且 $\int_{\left [ 0, 1\right ]}D\left ( x \right )dx=0$ ，而 $D\left ( x \right )$ 在 $\left [ 0,1 \right ]$ 上并不是黎曼可积的；
已知： $f\left ( x \right )$ 在 $E$ 上勒贝格可积 $\Leftrightarrow$ $f^+\left ( x \right ),f^-\left ( x \right )$ 在 $E$ 上均勒贝格可积；这也说明了： $f\left ( x \right )$ 在 $E$ 上勒贝格可积 $\Leftrightarrow$ $\left | f\left ( x \right ) \right |$ 在 $E$ 上均勒贝格可积；但黎曼积分不是这样的，比如： $h\left ( x \right )=\left\{\begin{matrix} \frac{1}{x}\sin\frac{1}{x}, &0<x\leqslant 1 \\ 0, & x=0 \end{matrix}\right.$ ， $h\left ( x \right )$ 在 $\left [ 0,1 \right ]$ 上黎曼可积但 $\left | h\left ( x \right ) \right |$ 在 $\left [ 0,1 \right ]$ 上不是黎曼可积的；

关系定理：有界函数 $f\left ( x \right )$ 在 $\left [ a,b \right ]$ 上是黎曼可积的 $\Rightarrow$ $f\left ( x \right )$ 在 $\left [ a,b \right ]$ 上是勒贝格可积的；且 $\int_{\left [ a,b\right ]}f\left ( x \right )dx=\int_{a}^{b}f\left ( x \right )dx$ ；故之后我们对 $f\left ( x \right )$ 在 $\left [ a,b \right ]$ 上的勒贝格积分，也记作 $\int_{a}^{b}f\left ( x \right )dx$ ；
关系详述：

根据一系列推导可知，勒贝格积分的性质与黎曼积分十分相似，证明的思想方法也十分相似；但勒贝格积分对可积性的要求比较低，对于有界函数而言，可测就行了；而一般可测函数的勒贝格积分定义看起来与广义黎曼积分有很大不同，但实际上两者之间有着内在联系：比如我们考察 $m\left ( x \right )=\frac{1}{x^p}\left ( 0<x<1,p>0 \right )$ 的黎曼可积性时，需要将瑕点 $x=0$ 挖掉考察 $\left [ \delta ,1 \right )\left ( \delta \rightarrow 0 \right )$ 的黎曼可积性，而考察勒贝格可积性通常是将函数截断，即作截断函数 $m_n\left ( x \right )=\left\{\begin{matrix} 0, &x\in \left ( 0,\frac{1}{n} \right ) \\ \frac{1}{x^p}, & x\in \left [\frac{1}{n},1 \right ) \end{matrix}\right.$ 考察其黎曼可积性，于是得到一个有界可测函数序列 $\left \{ m_n\left ( x \right ) \right \}$ ，它处处收敛到 $m\left ( x \right )$ ， $\left \{ m_n\left ( x \right ) \right \}$ 在 $\left ( 0,1 \right )$ 上的勒贝格积分与 $f\left ( x \right )$ 在 $\left [\frac{1}{n},1 \right )$ 上的黎曼积分是一样的，可见对于非负函数而言，两者本质上相同；
由于实变函数理论中允许函数取值为 $\infty$ ，当然也允许勒贝格积分取值为 $\infty$ ，所以在勒贝格积分中“可积”与“积分存在”是不同的概念；也正因为如此，一般可测函数的勒贝格积分通常是先定义非负函数的积分，再将一般函数分解成正部 $f^+$ 与负部 $f^-$ ，即令 $f^+=\frac{\left | f \right |+f}{2},f^-=\frac{\left | f \right |-f}{2}$ ，若 $f^+,f^-$ 的积分均为有限值，则称 $f\left ( x \right )$ 可积，若 $f^+,f^-$ 至少有一个有限，则称函数的积分存在，正是这个积分定义决定了 $f,\left | f \right |$ 勒贝格可积性的等价；