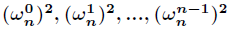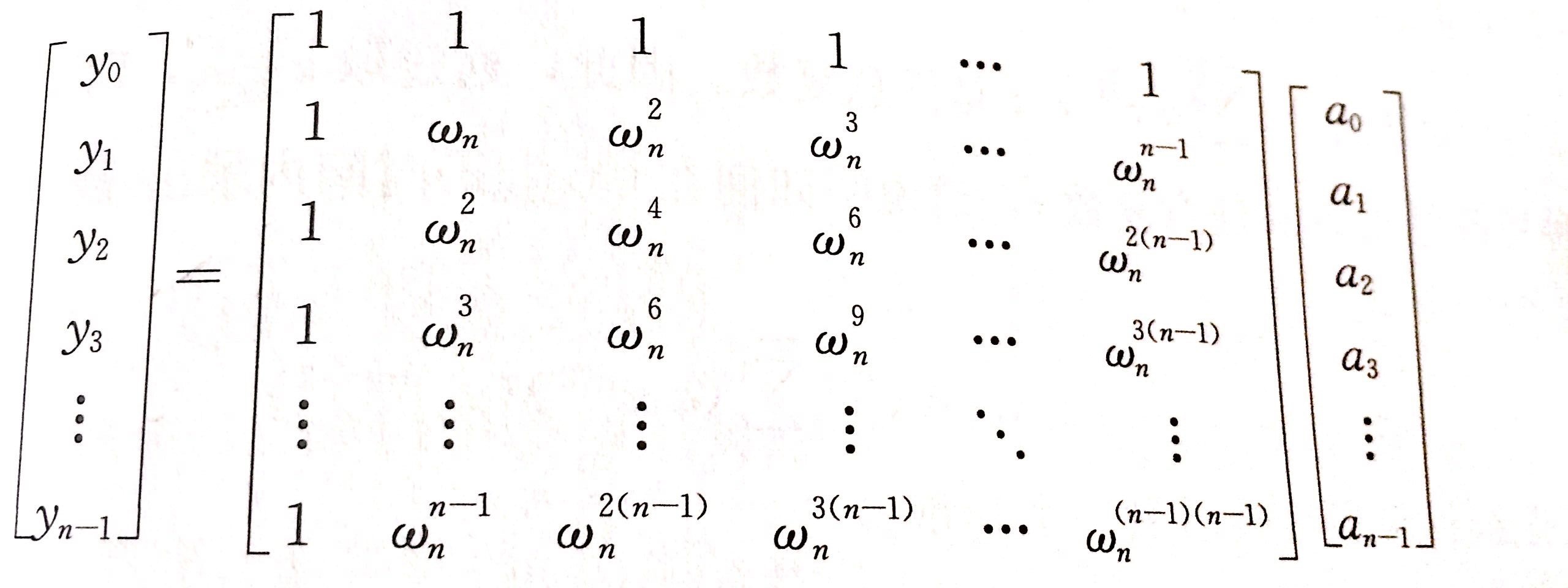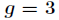多项式加法(5分)
题目内容:
一个多项式可以表达为x的各次幂与系数乘积的和,比如:
2x6+3x5+12x3+6x+20
现在,你的程序要读入两个多项式,然后输出这两个多项式的和,也就是把对应的幂上的系数相加然后输出。
程序要处理的幂最大为100。
输入格式:
总共要输入两个多项式,每个多项式的输入格式如下:
每行输入两个数字,第一个表示幂次,第二个表示该幂次的系数,所有的系数都是整数。第一行一定是最高幂,最后一行一定是0次幂。
注意第一行和最后一行之间不一定按照幂次降低顺序排列;如果某个幂次的系数为0,就不出现在输入数据中了;0次幂的系数为0时还是会出现在输入数据中。
输出格式:
从最高幂开始依次降到0幂,如:
2x6+3x5+12x3-6x+20
注意其中的x是小写字母x,而且所有的符号之间都没有空格,如果某个幂的系数为0则不需要有那项。
输入样例:
6 2
5 3
3 12
1 6
0 20
6 2
5 3
2 12
1 6
0 20
输出样例:
4x6+6x5+12x3+12x2+12x+40
时间限制:500ms内存限制:32000kb
#include <stdio.h>int main(void)
{int i,cnt; //设置循环变量i和计数器cnt(用于统计第一个输出,控制是否输出符号) int a[101]={0};int b[101]={0};int inpm,inpx;cnt=0; //初始化计数器 for(inpm=1;inpm!=0;) //获取第一个多项式,保存到数组a {scanf("%d %d",&inpm,&inpx); //inpm是幂次,对应数组的索引。inpx是系数,对应数组的值 a[inpm]=inpx;}for(inpm=1;inpm!=0;) //获取第二个多项式,保存到数组b {scanf("%d %d",&inpm,&inpx);b[inpm]=inpx;}for(i=0;i<=100;i++) //将两个多项式的同幂次系数相加 {a[i]+=b[i];}for(i=100;i>1;i--) //遍历99个数组 {if(a[i]==0) //系数是0就忽略 continue;if(a[i]==1||a[i]==-1) //当多项式属于特殊值(1或-1) {if(a[i]>0&&cnt>0) {printf("+x%d",i); //系数大于0 }else{printf("-x%d",i); //系数小于0 }cnt++;}else{ //当多项式系数不是特殊值 if(a[i]>0&&cnt>0){printf("+%dx%d",a[i],i);//系数大于0 }else{printf("%dx%d",a[i],i); //系数小于0}cnt++;} }if(a[i]!=0) //当幂次为1时(i=1){if(a[i]==1) //系数是1 {printf("+x");}else if(a[i]==-1){ //系数是-1 printf("-x");}else{printf("%+dx",a[i]); //系数不是特殊值 }cnt++;}if(a[0]>0&&cnt>0) //当不止一项且系数大于0时 {printf("+%d",a[0]);}else if(a[0]==0&&cnt>0) //当不止一项且系数小于0时 {printf("+%d",a[0]);}else{ //当只有一项时 printf("%d",a[0]);}return 0;
}感想:完全独立完成的,但对结果很不满意,程序主体很简单,创建了两个大小为101数组去存储两个多项式,用索引表示幂次,索引对应的值表示幂次对应的系数,但是为了输出要求的格式,对特殊情况做了大量判断选择,尽管后期进一步优化,也是差强人意。
我希望寻找更好的方法解决目前存在的问题:
1.程序的资源浪费严重,一开始就创建了固定大小的数组,但在实际操作中不一定会使用到如此多得空间。特别是题目中输入数据是从大到小,明显有更好的写法。因为目前程序对数据的输入完全没有排序要求。
2.为实现要求的输出格式,对输出的判断条件过多,希望能大大简化。
3.为了判断是否为第一个输出,引入了计数器cnt,并分散到了各个代码块,以便判断是否输出符号,希望移除计数器。
4.获取两个多项式的代码块几乎相同,希望能够合并。想过自定义函数,但感觉不是非常好。