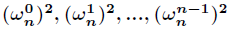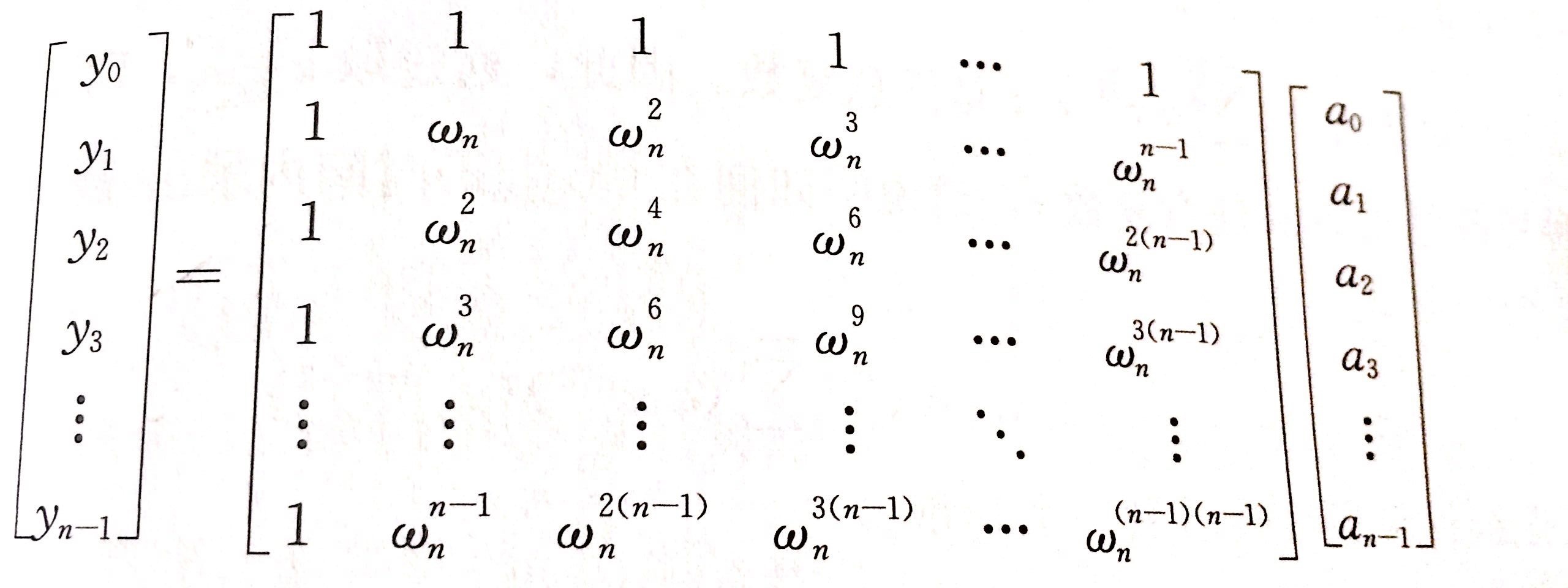我最初学习 $\text{FFT}$ 的资料是《小学生都能看懂的 $\text{FFT}$》。这当然可以助你快速起步。但说实在话，数学是很重要（也很有趣）的，你应该把复数当做需要掌握的知识点（而不是 $\text{FFT}$ 中的引理）。

还有 $\text{OI-wiki}$ 应该也能提供不少帮助。我当年完全不知道有这玩意儿。

前置知识：复数

引子：虚数

定义 $i$ 为使得 $i^2=-1$ 成立的值。一般我们把 $ki(k\in \mathbb{R})$ 叫做 虚数。

这个 $i$ 不是实数，因此也无法写成 $0.142857$ 或 $\cos (\Phi )$ 等等。我们只能保留这个 $i$ 。这就是一种记法而已。

不难发现，此时任意 $x<0$ 都可以定义 $\sqrt{x}=i\sqrt{-x}$，因此 $i$ 使得所有数的平方根都是有定义的。甚至 $i$ 也有平方根，这就会涉及到马上要讲的 复数。

如果你对域有所了解：这其实就是 $\mathbb{C}=\mathbb{R}(i)$ 括域的结果。然而了解域之前应该会先学复数吧。

定义

形如 $z=x+yi$ 的数字，我们称之为 复数。其 实部 为 $x$ 而 虚部 为 $y$ 。

我们可以用一个直角坐标系中的点 $(x,y)$ 表示 $z=x+yi$ 。发现和数轴类似，是一一对应关系。

由于是直角坐标系，也可以用幅角和模长的形式描述，即 $z=r\cdot (\cos \theta +i\sin \theta )$，其中 $\theta$ 是极角、$r$ 是长度（即 $r=\sqrt{x^2+y^2}$，为向量的模长）。

著名的欧拉公式 $e^{xi}=\cos x+i\sin x$ 则为我们提供了另一个表示法：$z=e^{\theta i}r$ 。我觉得欧拉公式是应该被了解的。

计算

那么 $z_1{z}_2$ 等于多少呢？设 $z_1=r_1\cdot (\cos {\theta }_1+i\sin {\theta }_1),z_2=r_2\cdot (\cos {\theta }_2+i\sin {\theta }_2)$，那么
$$\begin{array}{rl}{z}_1{z}_2& =r_1{r}_2\cdot [(\cos {\theta }_1\cos {\theta }_1-\sin {\theta }_1\sin {\theta }_1)+i(\sin {\theta }_1\cos {\theta }_2+\cos {\theta }_1\sin {\theta }_2)]\\ & =r_1{r}_2\cdot [\cos ({\theta }_1+{\theta }_2)+i\sin ({\theta }_1+{\theta }_2)]\end{array}$$

这告诉我们一个口诀：模长相乘，幅角相加。

当然，用欧拉公式表示法甚至用不到和差角公式，可以直接证明。

性质

首先，由于 幅角相加，所以 $x^n=1$ 有 $n$ 个取值。恰好把 $2\pi$ 的周角给 $n$ 等分。

上图为 $n=8$ 的情况。

用 ${\omega }_n$ 表示所有 $x$ 的解中，非零幅角最小的一个。也就是幅角为 $\frac{2\pi }{n}$、模长为 $1$ 的复数。这个 ${\omega }_n$ 被称为 “单位复根”。

明显有这几个性质：

• 可以同时扩倍，因为本质是比例关系。即

$${\omega }_n^k={\omega }_{n/2}^{k/2}$$

• 在环上，对面同样也有一个点。即 $n$ 为偶数时

$${\omega }_n^k=-{\omega }_n^{k+\frac{n}{2}}$$

• 转一圈就会回家。根据定义

$${\omega }_n^n=1$$

有关多项式

如果已知 $n$ 次多项式经过的 $(n+1)$ 个点，我们就可以建立方程，唯一确定这个多项式。可参考 拉格朗日插值。

为什么方程是线性无关的呢？如果你知道 $f(x_0)=f(x)\mathrm{mod}(x-x_0)$，并且你知道多项式是可以定义 $\gcd$ 的（也就是欧几里得环），那么 $\gcd (x-x_1,x-x_2)=1(x_1\ne x_2)$ 说明模数两两互质，根据 $\text{CRT}$ 我们可以还原解。

点值多项式相乘

假设 $f(x)$ 经过 $(x_0,a)$，而 $g(x)$ 经过 $(x_0,b)$，那么考虑 $h(x)=f(x)g(x)$，发现 $h(x_0)=f(x_0)g(x_0)=ab$，也就是说，$h(x)$ 经过 $(x_0,ab)$ 。

所以 点值多项式相乘是 $\mathcal{O}(n)$ 的。在一些情况下，这启发我们直接维护若干点值（完全忘却多项式的系数表示法）。

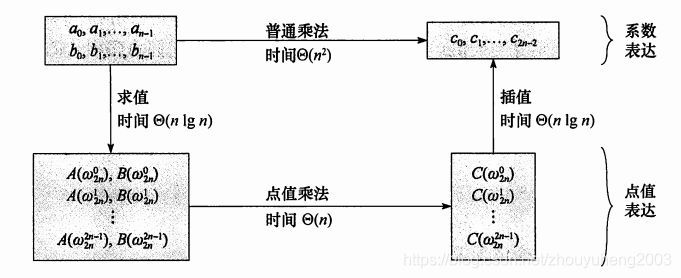
但是 $\text{FFT}$ 能够使得任意 $n$ 次多项式都能在 $\mathcal{O}(n\log n)$ 的时间内完成点值与系数表示的转化，因此获得了最快的多项式乘法方案。

大整数乘法

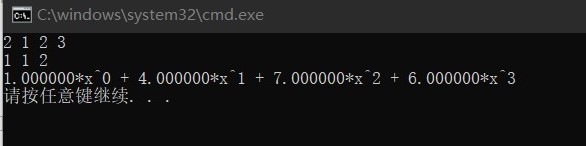
将各位数字视为系数，最后求 $f(10)$ 即可。

或者你可以这样说：本质都是卷积。

$\text{FFT}$

全称是 快速傅里叶变换（$\text{Fast Fourier Transform}$），高斯在 $1805$ 年（电脑问世之前）就发明了它。计算数学真恐怖。

但为什么叫傅里叶变换呢？这涉及到傅里叶级数
$$\begin{gathered} g(t)\sim \sum _{n=-\infty }^{+\infty }{f}_n\exp (2\pi int) \\ {f}_n:={\int }_{-\infty }^{+\infty }\exp (-2\pi int)g(t)\mathrm{d}t \end{gathered}$$

这或许是看 $\text{3b1b}$ 的绝佳借口。尽管其事实上并不干涉我们理解傅里叶变换。

因此我们对 $\frac{k}{n}(0⩽k<n)$ 做频率，提取傅里叶级数的系数，就得到离散傅里叶变换（$\text{Discrete Fourier Transform}$）。

离散傅里叶变换

通过计算 $f({\omega }_n^k)(0⩽k<n)$，我们得到了 $n$ 个点值。这就是 $\text{DFT}$ 正变换了。

我们可以把它轻易地变换回原系数。只需要以 $f({\omega }_n^k)$ 为 $x^k$ 的系数（得到 $n$ 次多项式）然后求 ${\omega }_n^{-k}$ 的点值得到
$$\begin{array}{rl}\sum _{j=0}^{n-1}f({\omega }_n^j)({\omega }_n^{-k}{)}^j& =\sum _{j=0}^{n-1}\sum _{t=0}^{n-1}{a}_t{\omega }_n^{jt}({\omega }_n^{-k}{)}^j\\ & =\sum _{t=0}^{n-1}{a}_t\sum _{j=0}^{n-1}{\omega }_n^{(k-t)j}\end{array}$$

后面那个关于 $j$ 的求和，是等比数列求和。当 $k=t$ 时公比为 $1$，显然和为 $n$ 。若 $k\ne t$，则该值为
$$\frac{{\omega }_n^{(k-t)n}-{\omega }_n^0}{{\omega }_n^{k-t}-1}=\frac{1-1}{{\omega }_n^{k-t}-1}=0$$

可以想到，这就是对 ${\int }_0^1\exp (2\pi int)\text{d}t=0$ 的离散模拟（这个叫法不严谨）。

因此，通过第二次插值，我们就可以得到原系数了。这就是逆变换。

完整地重复一遍结论：设 $f(x)={\sum }_{j=0}^{n-1}{a}_j{x}^j$，记 $g(x)={\sum }_{j=0}^{n-1}f({\omega }_n^j)x^j$，则
$$a_k=n^{-1}g({\omega }_n^{-k})$$

快速傅里叶变换

设
$$f(x)=\sum _{i=0}^{n-1}{a}_i{x}^i$$

其中 $n$ 为偶数。令
$$\begin{gathered} f_1(x)=a_0+a_{2}x+a_4{x}^2+\cdots +a_{n-2}{x}^{\frac{n}{2}-1} \\ {f}_2(x)=a_1+a_{3}x+a_5{x}^2+\cdots +a_{n-1}{x}^{\frac{n}{2}-1} \end{gathered}$$

那么
$$f(x)=f_1(x^2)+x{f}_2(x^2)$$

将 $x_j={\omega }_n^j$ 代入其中：
$$\begin{array}{rl}f({\omega }_n^j)& =f_1({\omega }_n^{2j})+{\omega }_n^j\cdot f_2({\omega }_n^{2j})\\ & =f_1({\omega }_{n/2}^j)+{\omega }_n^j\cdot f_2({\omega }_{n/2}^j)\end{array}$$

同理可得
$$\begin{array}{rl}f({\omega }_n^{j+n/2})& =f_1({\omega }_n^{2j+n})+{\omega }_n^{j+n/2}\cdot f_2({\omega }_n^{2j+n})\\ & =f_1({\omega }_{n/2}^j)-{\omega }_n^j\cdot f_2({\omega }_{n/2}^j)\end{array}$$

所以只需求解 $f_1,f_2$ 的 ${\omega }_{n/2}^j$ 处点值。这可以递归。复杂度 $T(n)=\mathcal{O}(n)+2T(\frac{n}{2})=\mathcal{O}(n\log n)$ 。

代码实现

蝴蝶变换

递归是耗费颇多的。我们研究一下划分系数的规律，以此去掉递归。

第一次划分，如果 $x$ 是奇数，那么就会 $+\frac{n}{2}$（分到右边）。然后 $x$ 成为了它所在那半边的第 $\lfloor \frac{x}{2}\rfloor$ 个系数。

对于第二次划分，如果 $\lfloor \frac{x}{2}\rfloor$ 是奇数，那么就会 $+\frac{n}{4}$（分到右边）。然后 $x$ 成为了 $\lfloor \frac{x}{4}\rfloor$ 。

一直到第 $i$ 次划分，如果 $\lfloor \frac{x}{2^{i-1}}\rfloor$ 是奇数，也就是二进制下第 $i$ 位（从 $1$ 开始编号）为 $1$，则走到的位置的二进制表示下第 $(n+1-i)$ 位为 $1$ 。

所以 将原下标二进制表示翻转，就是新位置的二进制表示。注意到移位先于所有计算，因此可以先移位，然后自底向上逐层模拟递归回溯前的计算。

计算 ${\omega }_n^{-x}$

由于 ${\omega }_n^{-x}={\omega }_n^{n-x}$，那么我们先求出 ${\omega }_n^x$ 作为自变量的点值。最后需要的点值 $b_x$ 对应的自变量是 ${\omega }_n^{-x}={\omega }_n^{n-x}$，也就是说第 $x$ 项应该放在第 $(n-x)$ 项处；直接将得到的点值数组的第 $1$ 到 $(n-1)$ 位翻转即可。

注意：如果只用 $\sin ,\cos$ 或者 $\exp$ 计算 ${\omega }_n^1$ 再自乘，速度较快；对于每一个都用三角函数求解，速度较慢，但是精度更高（事实上前者的精度损失也并不是很大）。

当然，因为我们已经把它预处理出来了，所以不需要上面所说的 $\mathtt{reverse}$ 的技巧；直接用 ${\omega }_n^{n-x}$ 代入，可以省去翻转的过程。

代码壹号

解释一下：我们预处理了幅角为 $\frac{2\pi }{n}$ 的单位复根的幂，现在对于长度为 $2w$ 的区间，相当于需要求出幅角为 $\frac{2\pi }{2w}$ 的单位复根。显然它就是 $\frac{2\pi }{n}\cdot \frac{n}{2w}$，也就是预处理数组中的第 $\frac{n}{2w}$ 位。

另外，这个代码不必背下来。因为后面会讲更好的写法。

using cplx = complex<double>; // in file <complex>
const double pi = acos(-1);
cplx omg[MAXN]; int went[MAXN];
/** @param opt 1 to DFT, -1 to IDFT */
void FFT(cplx a[], int n, int opt){const int N = 1<<n; // real lengthfor(int i=1; i!=N; ++i){went[i] = (went[i>>1]>>1)|((i&1)<<n>>1);if(i < went[i]) swap(a[i],a[went[i]]);}for(int i=1; i!=N; ++i){omg[i].real(cos(2*pi*i/N));omg[i].imag(sin(2*pi*i/N));}omg[0].imag(0), omg[0].real(1);for(int w=1; w!=N; w<<=1)for(cplx *p=a; p!=a+N; p+=(w<<1))for(int i=0; i<w; ++i){cplx t = omg[(N/(w<<1)*i*opt+N)%N];t = t*p[i+w], p[i+w] = p[i]-t, p[i] += t;}if(!(~opt)) for(int i=0; i!=N; ++i) a[i] /= N;
}

改进方案

精度提升

众所周知，$\mathtt{double}$ 的能力有限。哪怕是 $\mathtt{long}\mathtt{double}$，也有力不从心的时候。问题在于 数值太大，而过程中不能对值进行任何操作。尤其是对 $(10^9+7)$ 等大质数取模时，中途是不能取模的——毕竟涉及实数乘法。

如何防爆呢？核心肯定在于，减小结果的大小。要么减少数字个数，要么减小数字大小。对于第一个，考虑 $\mathtt{Karatsuba}$ 乘法，每次让数字个数变为 $\frac{1}{2}$，只能让结果变为 $\frac{1}{4}$ 。好像没有更好的方法了。此路不通。

那么怎么将数字减小呢？显然减法不行，考虑除法。实数除法也不行——数字变小了，但是小数点后的位数变多了，仍然存在精度问题。看来只有一条路了——整数除法，即整除。对某一个数作除法，照样无益；必须对所有数都作相同的除法。

比如除数是 $M$ 。那么一个数变为 $\lfloor \frac{a_i}{M}\rfloor M+(a_i\mathrm{mod}M)$，为了方便，记为 $v_{i}M+r_i$ 。于是 $a_i{b}_j=r_i{b}_j+(v_i{b}_j)M$ 。发现这两项的贡献是独立的，可以单独计算，最后相加！形式化地，写出两个新的多项式
$$\begin{gathered} f_{low}(x)=\sum _{i=0}^{n-1}\left(a_i\mathrm{mod}M\right)x^i \\ {f}_{high}(x)=\sum _{i=0}^{n-1}\lfloor \frac{a_i}{M}\rfloor x^i \end{gathered}$$

则 $f(x)g(x)=f_{low}(x)g(x)+M\cdot f_{high}(x)g(x)$ 。显然取 $M=\sqrt{\max a_i}$ 能够使得值下降的最快。如果对 $g(x)$ 再做一次此等拆分，则每个值的结果都在 $(\max a_i)\cdot n$ 以内，效果拔群！

另外说一句：一般都会对 $f(x),g(x)$ 同时作拆分，因为这样只需要 $4$ 次正变换、$3$ 次逆变换；如果封装过度，每次都调用 multiplies（将会调用 $2$ 次正变换、$1$ 次逆变换）就会变为 $8$ 次正变换、$4$ 次逆变换，大大的不好！

常数优化：二合一

如果我们要计算两个 系数为实数（虽然也基本上不可能是复数）的多项式 $A(x),B(x)$ 的乘积，似乎要做两次正变换？

可以这样：令 $P(x)=A(x)+iB(x),Q(x)=A(x)-iB(x)$，则只需要求出这两个的点值，相加除以二就是 $A$ 的点值，相减除以 $2i$ 就是 $B$ 的点值。

而二者的共轭关系，使得我们有 “二合一” 的方案。用 $\overline{z}$ 表示 $z$ 的共轭。
$$\begin{gathered} P({\omega }_n^k)=\sum _{j=0}^n(a_j+i{b}_j)\cdot {\omega }_n^{kj} \\ =\sum _{j=0}^n\overline{(a_j-i{b}_j){\omega }_n^{(n-k)j}}=\overline{Q({\omega }_n^{n-k})} \end{gathered}$$

当然你觉得这个很离谱，怎么就能够 “二合一” 呢？事实上，复数就是二元组，你相当于把两个数组放在一起变换罢了。所以你其实也可以用复数实现 “二合一” 的任意其他变换，但是效率可能并无提升，因为复数加法相较于实数加法就已经是两倍常数了。只是 $\text{FFT}$ 中，本来就是复数运算，所以是真正的常数优化。

注意上面的过程中，假定了 $(a_j+i{b}_j)$ 的共轭是 $(a_j-i{b}_j)$，所以必须要 $a_j,b_j\in \mathbb{R}$ 。

逆变换也可以 “二合一”，只要 原多项式系数是实数。假设我们已经知道 $A({\omega }^j),B({\omega }^j)$ 两个点值序列，则假设存在系数为复数的多项式 $P(x)$ 使得其点值为
$$P({\omega }^j)=A({\omega }^j)+iB({\omega }^j)$$

逆变换后，得到一个复系数多项式 $P(x)$ 。若将 $P(x)$ 的系数按照实部与虚部拆分，即 $P(x)=F(x)+i\cdot G(x)$，其中 $F(x),G(x)$ 系数均为实数，那么显然有 $P({\omega }^j)=F({\omega }^j)+iG({\omega }^j)$ 。

由于 $A(x),B(x)$ 系数均为实数，立刻可得 $\{\begin{array}{l}F(x)=A(x)\\ G(x)=B(x)\end{array}$ 是一组解。而 $F(x),G(x)$ 是唯一的（因为它们代表着 $P(x)$ 的系数拆分），所以这就是唯一解。所以 $P(x)$ 的系数的实部是 $A(x)$，而虚部是 $B(x)$，搞定！

常数优化：不蝴蝶变换

求点值的本质是乘了一个矩阵
$$\left(\begin{array}{cccc}{\omega }_n^{0\times 0}& {\omega }_n^{1\times 0}& \cdots & {\omega }_n^{n\times 0}\\ {\omega }_n^{0\times 1}& {\omega }_n^{1\times 1}& \cdots & {\omega }_n^{n\times 1}\\ ⋮& ⋮& \ddots & ⋮\\ {\omega }_n^{0\times n}& {\omega }_n^{1\times n}& \cdots & {\omega }_n^{n\times n}\end{array}\right)$$

而 $\text{FFT}$ 将其拆解为两个线性变换：将 $a_i$ 放到二进制位翻转后的 $i$ 的位置，称为蝴蝶变换；将蝴蝶变换后的序列进行各种操作，我们姑且称之为 “傅外叶变换” 吧。

考虑将上面的矩阵 转置。由于上面的矩阵是沿对角线对称的，所以转置不带来任何变化。但是对应到代码中，我们可以先进行 “傅外叶变换” 的转置，再进行蝴蝶变换的转置。而蝴蝶变换是交换位置，是沿对角线对称的，也没有区别。

做完这样的正变换之后，再做傅里叶变换（普通版）就可以把序列变回去。此时我们会发现：做傅里叶变换前需要一次蝴蝶变换，而做完 “傅外叶变换” 后也有一次蝴蝶变换。这不就相当于啥也没做嘛！

于是蝴蝶变换被抛弃了。蝴蝶变换是 $\text{random-access}$，常数较大，去掉它是一个不错的优化！

最后提一句，关于矩阵转置。傅里叶变换是自底向上，行向量 $(p_i,p_{i+L})$ 乘 $\left(\begin{array}{cc}1& 1\\ {\omega }^i& -{\omega }^i\end{array}\right)$，所以 “傅外叶变换” 是行向量 $(p_i,p_{i+L})$ 乘 $\left(\begin{array}{cc}1& {\omega }^i\\ 1& -{\omega }^i\end{array}\right)$，自顶向下进行。

typedef complex<double> fushu;
fushu omg[MAXN<<1];
void prepare(int n){for(int i=0; i<n; ++i){omg[i].imag(sin(2*M_PI*i/n));omg[i].real(cos(2*M_PI*i/n));}
}
void FFT(fushu a[],int n){const fushu *end_a = a+n;for(int w=n>>1,x=1; w; w>>=1,x<<=1)for(fushu *p=a; p!=end_a; p+=(w<<1))for(int i=0; i<w; ++i){const fushu l = p[i], r = p[i+w];p[i] = l+r, p[i+w] = (l-r)*omg[x*i];}
}
void DFFT(fushu a[],int n){const fushu *end_a = a+n;for(int w=1,x=n>>1; x; w<<=1,x>>=1)for(fushu *p=a; p!=end_a; p+=(w<<1))for(int i=0; i<w; ++i){fushu t = p[i+w]*omg[x*i];p[i+w] = p[i]-t, p[i] += t;}std::reverse(a+1,a+n);for(int i=0; i<n; ++i) a[i] /= n;
}

提醒：如果混用

本来我这里写的是 “不能混用”，然后被 $\mathsf{Quack}$ 光速打脸了……握巢，这摸猛犸？

能不能混用 不做蝴蝶变换 和 二合一 呢？可以，但是稍微麻烦一点点。注意到 不做蝴蝶变换 等价于多做了一次蝴蝶变换，所以此时 ${\omega }_n^x$ 对应的点值实际上放在 $\text{rev}(x)$ 的位置。而 二合一 需要我们找到 ${\omega }_n^{n-x}$ 的点值，也就是 $\text{rev}(n-x)$，然后放到 $\text{rev}(x)$ 去。怎么办？

别忘了 $n=2^k$，所以 $n-x$ 其实就是 $x$ 保留 $\text{lowbit}$，然后高位按位取反（假设是 $k$ 位二进制数）。于是 $\text{rev}(n-x)$ 其实就是 $\text{rev}(x)$ 保留 $\text{highbit}$，然后低位按位取反。预处理 $\text{highbit}$ 就可以做到了。

再探 $\text{FFT}$

可参考论文《再探快速傅立叶变换》和 $\mathsf{TLY}$ 太阳神 的 《课余时间的思考》。

重新理解

循环卷积的本质是对 $(x^n-1)$ 取模。而
$$x^n-1=\prod _{j=0}^{n-1}(x-{\omega }_n^j)$$

是其唯一分解。因此对 $(x-{\omega }_n^j)$ 分别取模，再做 $\text{CRT}$ 即可。也许你可以参考兔兔的博客。

$\text{Chirp-Z Transform}$

也被称为 $\text{Bluestain}$ 算法。目标是计算 $f(x^m)(m\in [0,n])$ 。通过 $mi=\left(\genfrac{}{}{0ex}{}{m+i}{2}\right)-\left(\genfrac{}{}{0ex}{}{m}{2}\right)-\left(\genfrac{}{}{0ex}{}{i}{2}\right)$，可以构造成卷积形式：
$$\begin{array}{rl}f(x^m)& =\sum _{i=0}^{n-1}{x}^{mi}{a}_i\\ & =\sum _{i=0}^{n-1}{x}^{\left(\genfrac{}{}{0ex}{}{m+i}{2}\right)-\left(\genfrac{}{}{0ex}{}{m}{2}\right)-\left(\genfrac{}{}{0ex}{}{i}{2}\right)}\times a_i\\ & =x^{-\left(\genfrac{}{}{0ex}{}{m}{2}\right)}\sum _{i=0}^{n-1}{x}^{-\left(\genfrac{}{}{0ex}{}{i}{2}\right)}{a}_i\times x^{\left(\genfrac{}{}{0ex}{}{m+i}{2}\right)}\end{array}$$

那么，想要实现任意长度的循环卷积，只需要将 $x=e^{\frac{2\pi }{n}}$ 代入。时间复杂度 $\mathcal{O}(n\log n)$ 。

$\text{NTT}$

全称是 $\text{Number Theoretic Transform}$，数论变换。

它的快速变换和离散变换拥有相同的名字，好奇怪哦。

引子：原根

如果 $g^{\phi (p)}\equiv 1(\mathrm{mod}p)$ 且最小的使得 $g^k\equiv 1(\mathrm{mod}p)$ 的正整数 $k=\phi (p)$，那么称 $g$ 是 $p$ 的原根。

特别地，上文中的 $k$ 被称为 阶（$\text{ord}$），但这不是我们要讨论的内容。

欧拉证明了 $2,4,p^k,2p^k(k⩾1)$ 有原根，其中 $p$ 是奇素数。

模仿 $\text{FFT}$

只要满足单位根的若干形式，一切结论都仍然成立。而单位根的本质是 ${\omega }_n^n=1$，所以等比数列求和会得到 $0$ 。

那么，有了原根 $g$，发现 $g^{\phi (p)}\equiv 1$，所以定义 ${\omega }_n=g^{\frac{\phi (p)}{n}}(n\mid \phi (p))$，就可以完全像 $\text{FFT}$ 那样进行卷积了。而且所有运算都在整数域（取模的剩余系）下运算，无任何精度误差！

同时我们也发现一个 局限性：$\phi (p)$ 需要含有足够多的 $2$ 的次幂，因为 $n\mid \phi (p)$ 时才有定义。最常见的是 $p=998244353$，此时 $2^{23}\mid \phi (p)$，基本上不会超！

代码实现被放在了多项式运算里，这里就不再贴出。

改进：任意模数

要是模数没有原根怎么办？注意到求出的系数不应超过 $a^{2}n$，因此另找 $3$ 个较大模数，用中国剩余定理合并，模意义下也能得到正确结果。

合并的时候好像还会爆 $\mathtt{long}\mathtt{long}$，怎么办？

假设已知
$$\{\begin{array}{l}x\equiv c_1(\mathrm{mod}{m}_1)\\ x\equiv c_2(\mathrm{mod}{m}_2)\\ x\equiv c_3(\mathrm{mod}{m}_3)\end{array}$$

我们首先将前两者合并得到
$$x\equiv k(\mathrm{mod}{m}_1{m}_2)$$

于是我们假设 $x=t{m}_1{m}_2+k$，由第三个同余方程得 $t{m}_1{m}_2+k\equiv c_3(\mathrm{mod}{m}_3)$ 。移项则有

$$t\equiv (c_3-k)\cdot m_1^{-1}\cdot m_2^{-1}(\mathrm{mod}{m}_3)$$

这些运算都是模 $m_3$ 的，可以轻松进行。求出 $(t\mathrm{mod}{m}_3)$ 也就得到了 $x\equiv t{m}_1{m}_2+k(\mathrm{mod}{m}_1{m}_2{m}_3)$，此时对原模数取模即可。

$\text{CNTT}$

全称是 $\text{Complex NTT}$，复数论变换。他可以部分弥补取模 $(4k-1)$ 型的质数时 $\text{NTT}$ 的无力（虽然 任意模数 干翻一切，但是它难打而且慢）。

考虑在某个 $\mathbb{GF}(p^2)$ 中进行运算，因为此时原根的阶是 $(p^2-1)=(p+1)(p-1)$ 。如果 $(p+1)$ 里含有足够多的 $2$ 的幂次，就可以了。

注意到 $p\equiv 3(\mathrm{mod}4)$ 在高斯整数环 $\mathbb{G}=\mathbb{Z}(i)$ 中是素元，因此 $p\mathbb{G}$ 是素理想，即得 ${\mathbb{Z}}_p(i)=\mathbb{G}/p\mathbb{G}$ 是整环，结合有限性知其是域。所以在 ${\mathbb{Z}}_p(i)$ 上进行运算即可。但找原根就只能查表了吧。

其实也可以理解为，在多项式环 ${\mathbb{Z}}_p[x]$ 上，对 $(x^2+1)$ 取模。核心也在于 $(-1)$ 不是模 $p$ 的二次剩余，因此 $(x^2+1)$ 是欧几里得环 ${\mathbb{Z}}_p[x]$ 上不可约元素，整环性即证。

定理：交换幺环 $R$ 上 $\text{DFT}$ 可逆的充要条件是 $({\omega }^k-1)(1⩽k<\phi )$ 可逆，其中 $\phi$ 是原根 $\omega$ 的阶。

解释：其充分性是显然的，必要性暂时不清楚，故留作习题。

$\text{64-bit}$ 整数的卷积

模 $2^{64}$ 意义下做卷积。

定义环 $R:=\mathbb{Z}\mathrm{mod}{2}^{64}$ 即 $R:=\mathbb{Z}/2^{64}\mathbb{Z}$ 。

将环 $R$ 拓展到 $T:=R[\omega ]\mathrm{mod}({\omega }^2+\omega +1)$ 。立方差公式不难验证 ${\omega }^3=1$ 。

现在考虑在 $T[x]\mathrm{mod}(x^n-\omega )$ 中做卷积，其中 $n$ 是 $3$ 的幂。

令 $y:=x^m$ 满足 $mr=n$ 且 $m⩾r$ 。则原多项式 $\sum a_i{x}^i$ 可以写为
$$\sum _{j=0}^{r-1}{y}^j\sum _{i=0}^{m-1}{a}_{jm+i}{x}^i$$

将其视为关于 $y$ 的多项式，认为其系数是 $T[x]\mathrm{mod}(x^{2m}+x^m+1)$，这样显然不会丢失信息。于是我们现在在做 $T[x][y]\mathrm{mod}(x^{2m}+x^m+1)\mathrm{mod}(y^r-\omega )$ 的卷积，因为 $y^r=x^n$ 。

为什么要对 $x$ 的多项式取模呢？因为
$$x^{2m}+x^m+1=(x^m-\omega )(x^m-{\omega }^2)$$

我们只需分别对二者取模，然后用 $\text{CRT}$ 合并即可。

该 $\text{CRT}$ 是简单的：设原本为 $(a+b{x}^m)$，对前者、后者取模分别得到 $f,g$，有关系式
$$\{\begin{array}{l}f=a-b\omega \\ g=a-b{\omega }^2\end{array}⟹\{\begin{array}{l}a=\frac{\omega f-g}{\omega -1}\\ b=\frac{f-g}{{\omega }^2-\omega }\end{array}$$

Comment. $\mathrm{CF}$ 帖子中似乎给出了奇怪的计算式，我不太理解。

最重要的是：此时都有 $x^{3m}={\omega }^3=1$，即 $x$ 是 $3m$ 次单位根！

所以对 $y$ 的循环卷积可行。可惜我们在对 $(y^r-\omega )$ 取模，因此要换元。

若现在对 $(x^m-\omega )$ 取模，那么换元 $z:=x^{\frac{2m}{r}}y$ 有 $z^r={\omega }^2{y}^r$，只需对 $(z^r-1)$ 取模即可。

若现在对 $(x^m-{\omega }^2)$ 取模，则换元 $z:=x^{\frac{m}{r}}y$ 同理。这也是要求 $m⩾r$ 的原因。

于是我们有能力作 $\text{FFT}$ 了。但点值相乘是 $T[x]\mathrm{mod}(x^m-\omega )$ 内的卷积。所以我们需要递归解决。

反正 ${\omega }^2$ 和 $\omega$ 没有本质区别，或者你可以认为是共轭的关系。

分析复杂度。$\text{FFT}$ 复杂度为 $\mathcal{O}(n\log n)$，点值相乘复杂度为 $2r\mathcal{T}(m)$，取 $m=r=\sqrt{n}$ 有 $\mathcal{T}(n)=2\sqrt{n}\mathcal{T}(\sqrt{n})+\mathcal{O}(n\log n)=\mathcal{O}(n\log n\log \log n)$ 。

Comment. 注意 $n⇝\sqrt{n}$ 的递归会使得 $\log n$ 除以 $2$，因此刚好和递归系数中的 $2$ 抵消。由递归层数 $\log \log n$ 即得。

Remark. 我们其实可以在任意代数结构上做卷积，但我还没看懂，因此只能贴个链接。