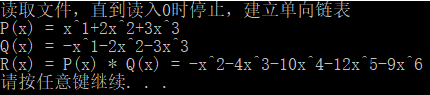多项式乘法

• 简介
  • 多项式的运算表示是一个很常见的算法问题。
• 问题描述
  • 给予两个多项式A(x)与B(x)，得出C(x)=A(x)B(x)。
  • 例如，A(x)=3+2x+3x^2+4x3，B(x)=2+x^{2，C(x)=6+4x+9x}2+10x^3+3x4+4x^5。
• 问题分析
  • 一般情况下，使用系数表示多项式，不存在的项系数为0。但是，除了系数表示外，多项式还有一种表示叫做点值表示。
  • 若多项式的度数为n，也就是多项式含有x^n项，则多项式可以被n+1对点值表示，前提是点不重复。
    • 举例如下
      • A(x)=3+2x+3x^2+4x^3
      • 取四个点:x=(0, 1, 2, 3)
      • 点值对:(0, 3), (1, 12), (2, 51), (3, 144)
      • 以上四个点足以表示多项式A(x)，没有任何其他多项式拥有这四个点。
  • 当两个多项式相乘，只需要乘它们的点值对就可以得到结果多项式的点值表示。
    • 对例题
      • 多项式:A(x)=3+2x+3x^2+4x^3，B(x)=2+x^2
      • 取6个点:x=(-2, -1, 0, 1, 2, 3)
      • 点值对:A(x):(-2, -21), (-1, 0), (0, 3), (1, 12), (2, 51), (3, 144);B(x):(-2, 6), (-1, 3), (0, 2), (1, 3), (2, 6), (3, 11)
      • 点值乘积:C(x):(-2, -126), (-1, 0), (0, 6), (1, 36), (2, 306), (3, 1584)
      • 需要6个点，因为多项式C(x)度数为2+3=5。
  • 知道了如何将系数表示转换为点值表示、如何做多项式点值表示的乘法，就可以开始学习FFT（快速傅里叶变换）算法。FFT算法可以做如下工作。
    • 找到单位的n+1次根，总共有n+1个。
    • 通过分治快速计算A(x)与B(x)在这些单位根的值。
    • 将A(x)与B(x)的点值相乘，得到C(x)的点值表示。
    • 将C(x)的点值表示转换为系数表示。
  • FFT的要点在于选值。如果只是随便选n+1个点，那就需要逐个计算这些点对应的值。但是，可以利用单位根的特性，从而采取分治算法。关于FFT算法以及单位根特性不细说，具体见代码。
• 代码

  •   # -*-coding:utf-8-*-from cmath import pi, expdef FFT(A, w):length = len(A)if length == 1:return [A[0]]A_even = []A_odd = []for i in range(0, length // 2):A_even.append(A[2 * i])A_odd.append(A[2 * i + 1])F_even = FFT(A_even, w ** 2)F_odd = FFT(A_odd, w ** 2)x = 1values = [0 for i in range(length)]for i in range(0, length // 2):values[i] = F_even[i] + x * F_odd[i]values[i + length // 2] = F_even[i] - x * F_odd[i]x = x * wreturn valuesdef solver(A, B):length = len(A) + len(B) - 1n = 1while 2 ** n < length:n += 1length = 2 ** nA.extend([0 for i in range(length - len(A))])B.extend([0 for i in range(length - len(B))])w = exp(2 * pi * 1j / length)A_values = FFT(A, w)B_values = FFT(B, w)C_values = [A_values[i] * B_values[i] for i in range(length)]result = [int((x / length).real) for x in FFT(C_values, w ** -1)]while result[-1] == 0:del result[-1]return resultif __name__ == '__main__':input_A, input_B = [3, 2, 3, 4], [2, 0, 1]print("A", input_A)print("B", input_B)result = solver(input_A, input_B)print("C", result)

• 运行结果
  • 
• 补充说明
  • 具体代码可以查看我的Github，欢迎Star或者Fork
  • 对代码进行了一些修正
  • 参考书《你也能看得懂的Python算法书