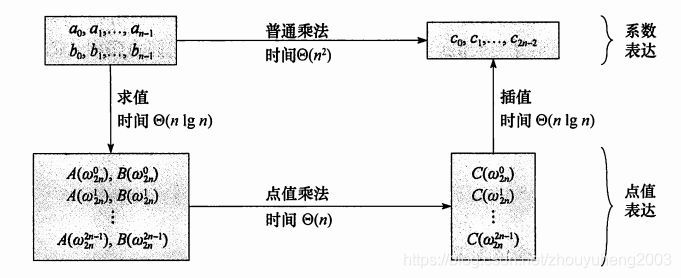
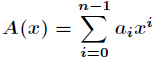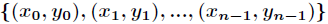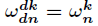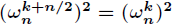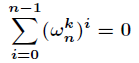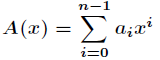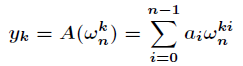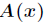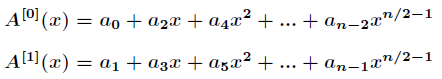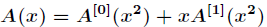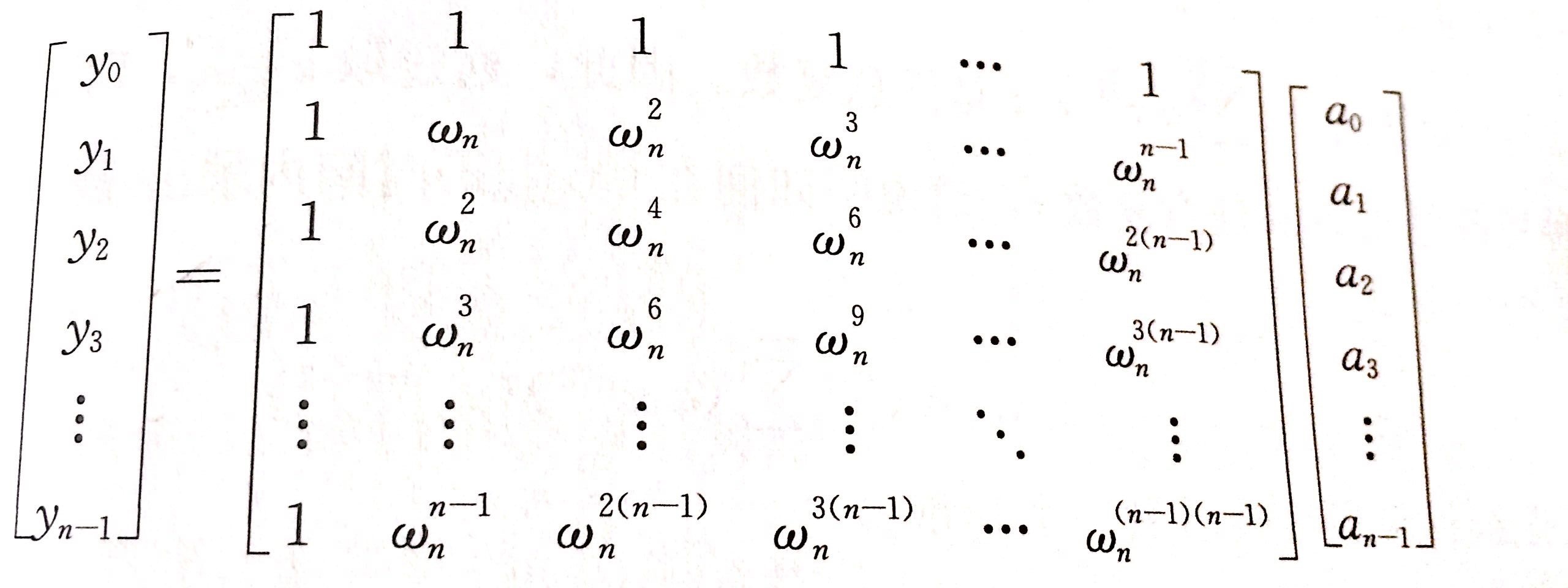多项式乘法运算初级版

快速傅里叶变换在信息学竞赛中主要用于求卷积，或者说多项式乘法。我们知道，多项式乘法的普通算法时间复杂度

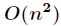
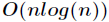
是，通过快速傅里叶变换可以使时间降为，那么接下来会详细介绍快速傅里叶变换的原理。

首先来介绍多项式的两种表示方法，即系数表示法和点值表示法。从某种意义上说，这两种方法是等价的。先设

（1）系数表示法

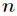
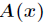
对于一个次数界为的多项式来说，其系数表示法就是一个由系数组成的向量，很

明显，这样的多项式乘法运算的时间复杂度为。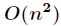

（2）点值表示法

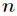
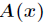
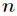
对于一个次数界为的多项式来说，其点值是个点值对所形成的集合

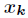
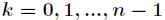
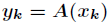
其中各不相同，并且当时，有。可以看出一个多项式可以有多种不同的点值

表示法，而通过这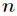个不同的点值对可以表示一个唯一的多项式。而通过点值表示法来计算多项式的乘法，时间

复杂度为。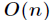

从原则上来说，计算多项式的点值是简单易行的，因为我们只需要先选取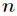个相异的点，然后通过秦九韶算法可

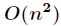
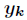
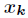
以在时间内求出所有的，实际上如果我们的选得巧妙的话，就可以加速这一过程，使其运行时间变

为。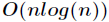

根据多项式的系数表示法求其点值表示法的过程称为求值，而根据点值表示法求其系数表示法的过程称为插值。

对于求卷积或者说多项式乘法运算问题，先是通过傅里叶变换对系数表示法的多项式进行求值运算，这一步的时

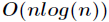
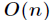
间复杂度为，然后在时间内进行点值相乘，再进行插值运算。

那么，接下来就是我们今天的重点了，如何高效地对一个多项式进行求值运算，即将多项式的表示法变为点值表示法。

如果选取单位复根作为求值点，则可以通过对系数向量进行离散傅里叶变换（DFT），得到相应的点值表示。同样地

也可以通过对点值对进行逆DFT运算，获得相应的系数向量。DFT和逆DFT的时间复杂度均为。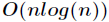

一. 求DFT

选取次单位复根作为来求点值是比较巧妙的做法。

次单位复根是满足的复数，次单位复根恰好有个，它们是，，为

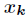
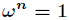
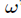
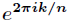
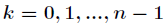
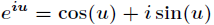
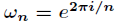
了解释这一式子，利用复数幂的定义，值称为主次单位根，所有其

它次单位复根都是的次幂。

个次单位复根在乘法运算下形成一个群，该群的结构与加法群模相同。

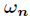
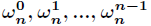
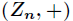
接下来认识几个关于次单位复根的重要性质。

（1）相消引理

对于任何整数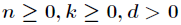，有

（2）折半引理

如果且为偶数，则

（3）求和引理

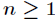
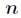
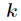
对任意整数和不能被整除的非零整数，有

回顾一下，我们希望计算次数界为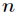的多项式

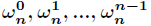
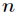
在处的值，假定是2的幂，因为给定的次数界总可以增大，如果需要，总可以添加值为零

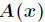
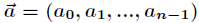
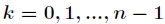
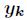
的新的高阶系数。假定已知的系数形式为，对，定义结果

如下

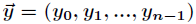
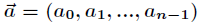
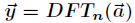
向量是系数向量的离散傅里叶变换，写作。

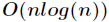
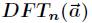
通过使用一种称为快速傅里叶变换（FFT）的方法，就可以在时间内计算出，而直接

计算的方法所需时间为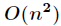，FFT主要是利用单位复根的特殊性质。FFT方法运用了分治策略，它用

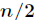
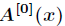
中偶数下标的系数与奇数下标的系数，分别定义了两个新的次数界为的多项式和

则进一步有

这样在处的值得问题就转换为求次数界为的多项式和在点

处的值。由于在奇偶分类时导致顺序发生变化，所以需要先通过Rader算法进行

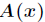
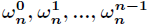
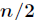
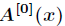
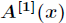
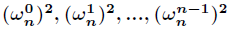
倒位序，在FFT中最重要的一个操作是蝴蝶操作，通过蝴蝶操作可以将前半部分和后半部分的值求出。

题目：http://acm.hdu.edu.cn/showproblem.php?pid=1402

题意：大数乘法，需要用FFT实现。

代码：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>using namespace std;
const int N = 500005;
const double PI = acos(-1.0);struct Virt
{double r, i;Virt(double r = 0.0,double i = 0.0){this->r = r;this->i = i;}Virt operator + (const Virt &x){return Virt(r + x.r, i + x.i);}Virt operator - (const Virt &x){return Virt(r - x.r, i - x.i);}Virt operator * (const Virt &x){return Virt(r * x.r - i * x.i, i * x.r + r * x.i);}
};//雷德算法--倒位序
void Rader(Virt F[], int len)
{int j = len >> 1;for(int i=1; i<len-1; i++){if(i < j) swap(F[i], F[j]);int k = len >> 1;while(j >= k){j -= k;k >>= 1;}if(j < k) j += k;}
}//FFT实现
void FFT(Virt F[], int len, int on)
{Rader(F, len);for(int h=2; h<=len; h<<=1) //分治后计算长度为h的DFT{Virt wn(cos(-on*2*PI/h), sin(-on*2*PI/h));  //单位复根e^(2*PI/m)用欧拉公式展开for(int j=0; j<len; j+=h){Virt w(1,0);            //旋转因子for(int k=j; k<j+h/2; k++){Virt u = F[k];Virt t = w * F[k + h / 2];F[k] = u + t;     //蝴蝶合并操作F[k + h / 2] = u - t;w = w * wn;      //更新旋转因子}}}if(on == -1)for(int i=0; i<len; i++)F[i].r /= len;
}//求卷积
void Conv(Virt a[],Virt b[],int len)
{FFT(a,len,1);FFT(b,len,1);for(int i=0; i<len; i++)a[i] = a[i]*b[i];FFT(a,len,-1);
}char str1[N],str2[N];
Virt va[N],vb[N];
int result[N];
int len;void Init(char str1[],char str2[])
{int len1 = strlen(str1);int len2 = strlen(str2);len = 1;while(len < 2*len1 || len < 2*len2) len <<= 1;int i;for(i=0; i<len1; i++){va[i].r = str1[len1-i-1] - '0';va[i].i = 0.0;}while(i < len){va[i].r = va[i].i = 0.0;i++;}for(i=0; i<len2; i++){vb[i].r = str2[len2-i-1] - '0';vb[i].i = 0.0;}while(i < len){vb[i].r = vb[i].i = 0.0;i++;}
}void Work()
{Conv(va,vb,len);for(int i=0; i<len; i++)result[i] = va[i].r+0.5;
}void Export()
{for(int i=0; i<len; i++){result[i+1] += result[i]/10;result[i] %= 10;}int high = 0;for(int i=len-1; i>=0; i--){if(result[i]){high = i;break;}}for(int i=high; i>=0; i--)printf("%d",result[i]);puts("");
}int main()
{while(~scanf("%s%s",str1,str2)){Init(str1,str2);Work();Export();}return 0;
}

题目：http://acm.hdu.edu.cn/showproblem.php?pid=4609

题意：给定n条长度已知的边，求能组成多少个三角形。

分析：用一个num数组来记录次数，比如num[i]表示长度为i的边有num[i]条。然后对num[]求卷积，除去本身重

复的和对称的，然后再整理一下就好了。

代码：

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>using namespace std;
typedef long long LL;const int N = 400005;
const double PI = acos(-1.0);struct Virt
{double r,i;Virt(double r = 0.0,double i = 0.0){this->r = r;this->i = i;}Virt operator + (const Virt &x){return Virt(r+x.r,i+x.i);}Virt operator - (const Virt &x){return Virt(r-x.r,i-x.i);}Virt operator * (const Virt &x){return Virt(r*x.r-i*x.i,i*x.r+r*x.i);}
};//雷德算法--倒位序
void Rader(Virt F[],int len)
{int j = len >> 1;for(int i=1; i<len-1; i++){if(i < j) swap(F[i], F[j]);int k = len >> 1;while(j >= k){j -= k;k >>= 1;}if(j < k) j += k;}
}//FFT实现
void FFT(Virt F[],int len,int on)
{Rader(F,len);for(int h=2; h<=len; h<<=1) //分治后计算长度为h的DFT{Virt wn(cos(-on*2*PI/h),sin(-on*2*PI/h));  //单位复根e^(2*PI/m)用欧拉公式展开for(int j=0; j<len; j+=h){Virt w(1,0);            //旋转因子for(int k=j; k<j+h/2; k++){Virt u = F[k];Virt t = w*F[k+h/2];F[k] = u+t;      //蝴蝶合并操作F[k+h/2] = u-t;w = w*wn;      //更新旋转因子}}}if(on == -1)for(int i=0; i<len; i++)F[i].r /= len;
}//求卷积
void Conv(Virt F[],int len)
{FFT(F,len,1);for(int i=0; i<len; i++)F[i] = F[i]*F[i];FFT(F,len,-1);
}int a[N];
Virt F[N];
LL num[N],sum[N];
int len,n;void Init()
{memset(num,0,sizeof(num));scanf("%d",&n);for(int i=0; i<n; i++){scanf("%d",&a[i]);num[a[i]]++;}sort(a, a + n);int len1 = a[n-1] + 1;len  = 1;while(len < len1*2) len <<= 1;for(int i=0; i<len1; i++)F[i] = Virt(num[i],0);for(int i=len1; i<len; i++)F[i] = Virt(0,0);
}void Work()
{Conv(F,len);for(int i=0; i<len; i++)num[i] = (LL)(F[i].r+0.5);len = a[n-1]*2;for(int i=0; i<n; i++)num[a[i]+a[i]]--;for(int i=1; i<=len; i++)num[i] >>= 1;sum[0] = 0;for(int i=1; i<=len; i++)sum[i] = sum[i-1] + num[i];LL cnt = 0;for(int i=0; i<n; i++){cnt+=sum[len]-sum[a[i]];//减掉一个取大，一个取小的cnt-=(LL)(n-1-i)*i;//减掉一个取本身，另外一个取其它cnt-=(n-1);//减掉大于它的取两个的组合cnt-=(LL)(n-1-i)*(n-i-2)/2;}LL tot = (LL)n*(n-1)*(n-2)/6;printf("%.7lf\n",(double)cnt/tot);
}int main()
{int T;scanf("%d",&T);while(T--){Init();Work();}return 0;
}