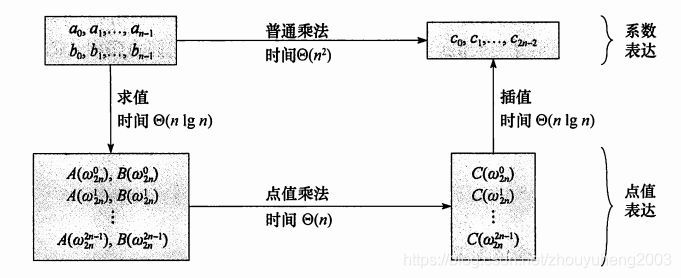
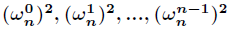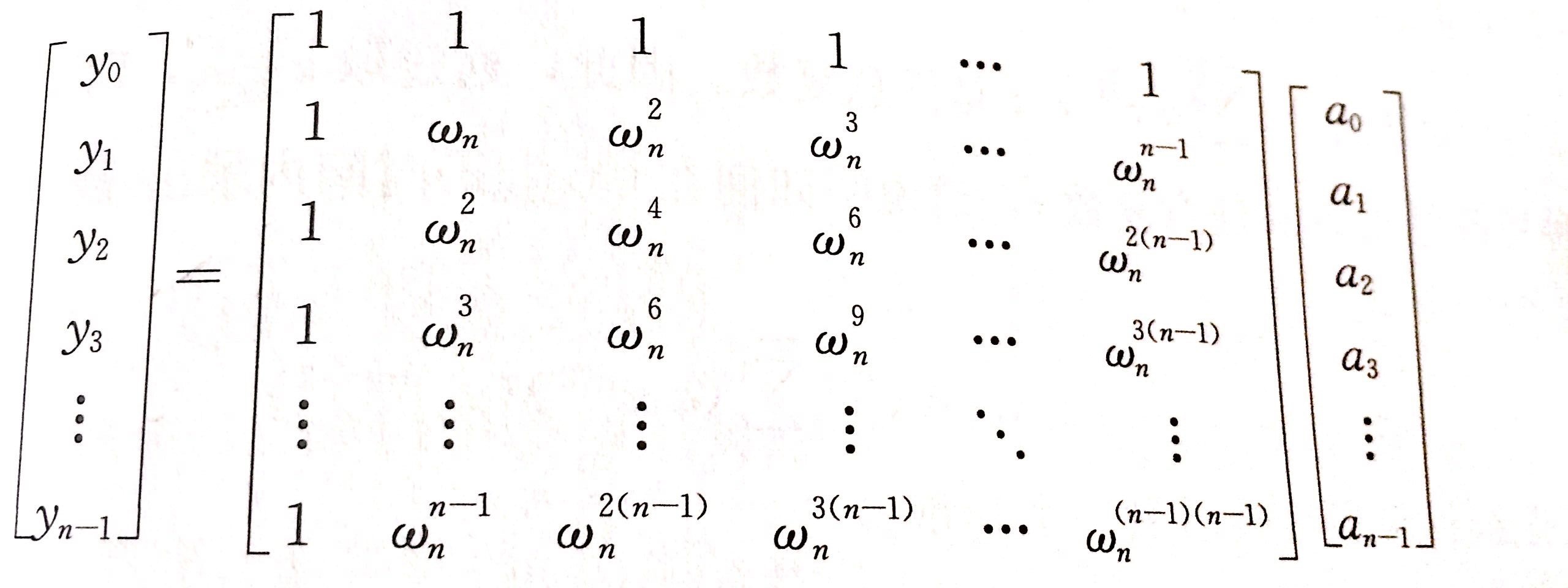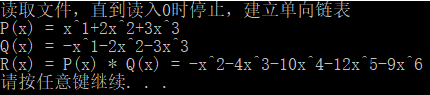多项式乘法

什么是多项式？

由若干个单项式相加组成的代数式叫做多项式（若有减法：减一个数等于加上它的相反数）。
多项式中的每个单项式叫做多项式的项，这些单项式中的最高项次数，就是这个多项式的次数。 多项式中不含字母的项叫做常数项。

在C语言中怎么表示？

最简单直观的方式就是：

将多项式对应的系数储存在数组中，而数组下标就是项的指数

最后写出相应的代码

#include <stdio.h>int main()
{int i, j, m, n;scanf("%d", &m);double a[m + 1];for (i = 0; i <= m; i++)scanf("%lf", &a[i]);scanf("%d", &n);double b[n + 1];for (i = 0; i <= n; i++)scanf("%lf", &b[i]);double c[m + n + 1];for (i = 0; i <= m + n; i++)c[i] = 0;for (i = 0; i <= m; i++)for (j = 0; j <= n; j++)c[i + j] += a[i] * b[j];printf("%f*x^%d", c[0], 0);for (i = 1; i <= m + n; i++)printf(" + %f*x^%d", c[i], i);return 0;
}

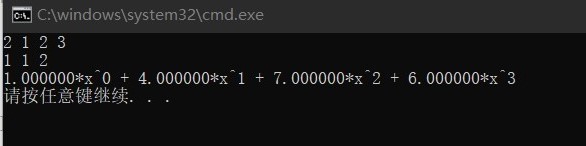
测试一下

例如

(1 + 2x + 3x ^2)·(1 + 2x)=1 + 4x + 7x ^2 + 6x ^3

结果

下一篇：多项式除法

https://blog.csdn.net/m0_52313753/article/details/112585857