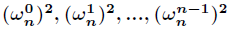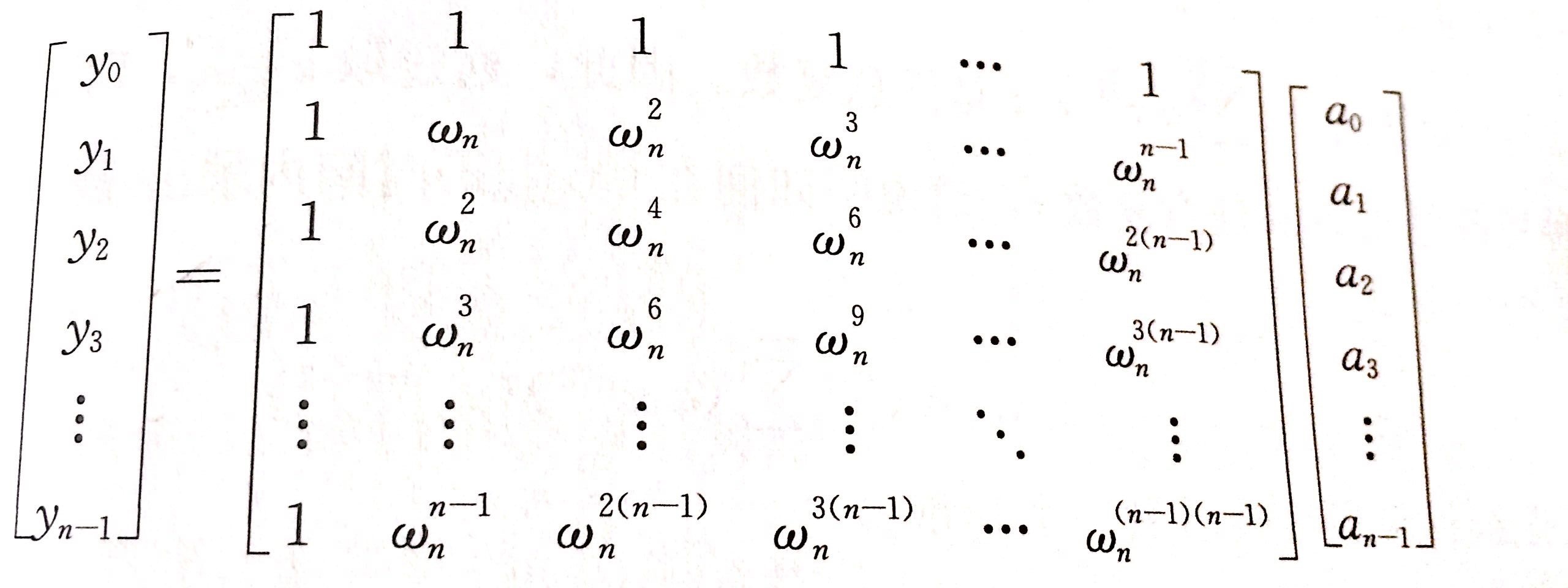多项式乘法入门

By SemiWaker

这是一篇蒟蒻对FFT、DFT、CZT、NTT的弱鸡理解

多项式

$$a_0x+a_1x^1+a_2x^2\cdots+a_{n-1}x^{n-1}$$
上面的这个形式叫做多项式。
系数： $a_{0..n-1}$
项： $a_ix^i$
界：n
为了方便我们系数序列就可以表示多项式。

线性卷积

$$A\times B=\sum_{i=0}^{2n-2}(\sum_{j=0}^{i}A_jB_{i-j})x^i$$
简单来说，就是把两个多项式直接乘起来。
第i项的构成如下：
任取两个项 $A_jx^j$和 $B_kx^k$，如果 $j+k=i$，那么得到 $A_jB_kx^i$。
将所有 $j+k=i$的项系数两两相乘加起来即可。

循环卷积

$$A\times B=\sum_{i=0}^{n-1}(\sum_{j,k}A_jB_k[j+k\equiv i\pmod n])x^i$$
比较难理解。
其实就是把多项式的-1项设为n-1项，-2项设为n-2项……
然后，线性卷积为了防止出现-1项，设定了j<=i，现在我们把它去掉。
$$A\times B=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}A_jB_{i-j})x^i$$

线性卷积和循环卷积关系

我们用比较形象地方式说明。
举个例子

$$(1+2x+3x^2+4x^3)\times(5+6x+7x^2+8x^4)$$
即 $(1,2,3,4)\times(5,6,7,8)$
线性卷积：

循环卷积

如果把 (5,6,7,8) 复制展开

然后我们观察，设线性卷积的结果为 $C_{0...6}$，循环卷积的结果为 $D_{0..3}$
则有：
$D_0=C_0+C_4$
$D_1=C_1+C_5$
$D_2=C_2+C_6$
$D_3=C_3$
也就是说，把线性卷积重叠在一起，就得到了循环卷积。

多项式点值表示

我们把N个数$x_{0..n-1}$带入x，可以得到多项式的N个值$A(x_{0..n-1})$。
将每一个数和对应的值当成一个点$(x_i,A(x_i))$，这N个点叫做多项式的点值表示。
为什么点值表示可以代表多项式呢?
因为我们可以反过来用点值表示求出多项式。
待定系数+解方程就可以了。

多项式插值

就是把点值表示转换成系数表示的一个过程。

DFT

离散傅里叶变换
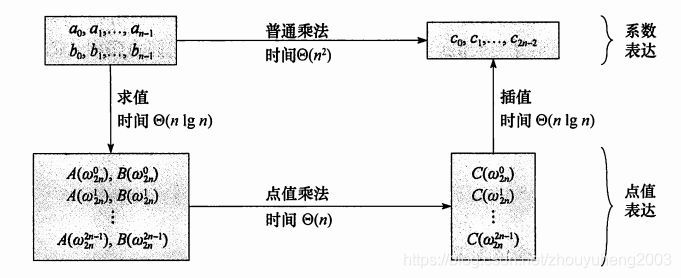
考虑怎样快速求多项式卷积。
按照定义去写$O(n^2)$，显然不优。

我们可以考虑点值表示。
两个多项式如果取值用的是同样的数$x_{0..n-1}$，那么得到的值直接乘起来就可以得到卷积之后的多项式的点值表示。

但是如果按照定义一个一个数带入求多项式的值，还是$O(n^2)$的，没有优化。

我们考虑带入特殊的数去求点值表示。

DFT就是这样一个过程：将一个多项式转化为用n次单位根表示的点值表示。

FFT是实现DFT的算法。

单位根

简单来说$x^n=1$的复数解。
n次单位根有n个复数解，设为$\omega_n^k$，其中k=0…n-1。
$\omega_n^k=e^{\frac {2k\pi I}n}$
用欧拉公式展开：
$e^{xI}=cos(x)+sin(x)I$
得到
$(\omega_n^k)^n=cos(2k\pi)+sin(2k\pi)I=1$

画在复数平面上，刚好是把单位元n等分的n个点。

有一些有趣的性质
$\omega_n^k=\omega_n^{k\pmod n}$
由三角函数周期性可证。
$\omega_n^{\frac n2}=-1$
显然。
$\omega_n^n=1$
显然。
$\omega_n^k=\omega_{\frac n2}^{\frac k2}$
显然。
$(\omega_n^k)^2=(\omega_n^{k+\frac n2})^2$
把定义带入可证。

FFT的实现

快速傅里叶变换 Cooley-Tukey算法
考虑把$\omega_n^{0...n-1}$一起带入求值。

则

$$A_k=\sum_{j=0}^{n-1}a_j(\omega_n^k)^j$$
可以分治为两部分
$$A_k=\sum_{j=0}^{\frac {n-1}2}a_{2j}(\omega_n^k)^{2j}+(\omega_n^k)\sum_{j=0}^{\frac {n-1}2}a_{2j+1}(\omega_n^k)^{2j}$$
两半的长度都为 $\frac n2$

而$(\omega_n^k)^{2j}=(\omega_n^{k+{n/2}})^{2j}=\omega_{\frac n2}^{kj}$
所以而$\omega_{\frac n2}^{kj}$只有$\frac n2$个取值，而且每个出现两次。

这样就通过分治减小了规模。

现在变成了对两个多项式$(a0,a2,a4...)$和$(a1,a3,a5...)$求带入$\omega_{\frac n2}^{0..\frac n2-1}时的值$。

分治完了之后，我们要求回原来的多项式。
设分治的结果为$B_{0..\frac n2-1}$和$C_{0..\frac n2-1}$。
则$A_k=B_k+\omega_n^kC_k$
但是注意此时k只有$\frac n2$
所以$A_{k+\frac n2}=B_k+\omega_n^{k+\frac n2}C_k$
又$\omega_n^{k+\frac n2}=-\omega_n^k$
所以$A_{k+\frac n2}=B_k-\omega_n^kC_k$

用一个简单的图来记：

设当前分治长度为L，则
$A_k=A_k+\omega_n^kA_{k+\frac L2}$
$A_{k+\frac L2}=A_k-\omega_n^kA_{k+\frac L2}$
注意变量自我迭代时，要开临时变量
这两个位置刚好交错计算，形状类似蝴蝶，所以叫做蝴蝶变换。

边界：
n=1时，$\omega_1^1=1$，所以直接把$a_k$放进去就好了。

程序怎么实现呢？
直接分治是可以的，但是有更好的方法。
我们考虑分治时的分类方法：
每一层按照奇偶数。
如果我们保持编号不变，那么就变成：第i行按照从低到高第i位分。
由于是从低到高，所以最后的排列为：每一个数的位置，为编号二进制倒序后位置。
举例：有8个数，编号0~7。
分治过程：
000 001 010 011 100 101 110 111
000 010 100 110|001 011 101 111
000 100|010 110|001 101|011 111
000|100|010|110|001|101|011|111

把最后一行的二进制倒过来：
000 001 010 011 100 101 110 111
刚好是从0~7。

设Reverse(x)为x二进制倒序后的数
一开始我们可以将ai放到Reverse(i)的位置。

然后设当前层分治长度为L。
每L个一起处理，进行蝴蝶变换即可。

进一步优化，注意蝴蝶变换中$\omega_n^k$的k取值为0~L/2
为了尽量减少对$\omega_n^k$的计算次数，我们可以先枚举0~L/2，计算$\omega_n^k$，然后枚举每一个分治块的相应位置进行蝴蝶变换。

IDFT

逆离散傅里叶变换
求出点值表示，再相乘之后，我们要进行插值操作。
通过对DFT求逆矩阵，我们直接给出以下结论：
将点值表示$(A_0,A_1...A_n)$转换为系数表示$(a_0,a_1...a_n)$，只需要求出：

$$a_i=\frac{\sum_{i=0}^{n-1}A_i(\omega_n^k)^{-i}}n$$
换句话说，我们要把DFT中的每一个 $\omega_n^k$换成 $\omega_n^{-k}$，然后除以n即可。

代码

void FFT(Complex *A,int n,int sgn)
{for (int i=1;i<n-1;++i){int j=0;for (int t=1,k=i;t<n;t<<=1,j=((j<<1)|(k&1)),k>>=1);if (j>i) swap(A[i],A[j]);}for (int L=2;L<=n;L<<=1){int L1=L>>1;for (int i=0;i<L1;++i){Complex w=Complex(cos(sgn*PI*i/L1),sin(sgn*PI*i/L1));for (int j=i;j<n;j+=L){int k=j+L1;Complex u=A[j],v=w*A[k];A[j]=u+v;A[k]=u-v;}}}if (sgn==-1) for (int i=0;i<n;++i) A[i]=A[i]/Complex(n,0.0);
}

至于是用exp还是直接两个三角函数，一个exp应该是快些，但是只能用STL的complex。如果要手写complex就只能两个三角函数。手写会快些。
注意：因为要对2分治，所以要强行把项数补到$2^n$，后面的项系数为0。如果是两个长度为n的多项式相乘，那么至少要开4n的空间。

循环卷积和线性卷积对于DFT的区别

线性卷积卷得到项数是2n-1，而循环卷积得到的项数是n。
那么我们在求点值表示的时候，线性卷积就带入2n-1个点，循环卷积就带入n个点，再相应的IDFT出来的结果就是所求的结果。

CZT

Z-变换
在用FFT的过程中，我们要强行把多项式补到$2^n$项。那么，FFT出来的点值表示，实际上和原来的点值表示已经不一样了。（因为n变了）
在求线性卷积的时候，补足$2^n$项没有什么问题。但是如果要求循环卷积，补足$2^n$位就会产生很大的问题。（定义决定的）

求循环卷积时，我们要保证项数不变，DFT出来的点值表示才能表示原来的循环卷积。

怎样保证项数不变呢？

考虑原来的公式

$$A_k=\sum_{j=0}^{n-1}a_j(\omega_n^k)^j$$
即 $$A_k=\sum_{j=0}^{n-1}a_je^{\frac {2\pi jk}nI}$$

考虑我们把jk变换一下。
其实是更加复杂了
$jk=\frac {j^2+k^2-(j-k)^2}2$
然后带入

$$A_k=\sum_{j=0}^{n-1}a_je^{\frac {\pi( j^2+k^2-(j-k)^2)}nI}$$
稍微变化下
$$A_k=e^{\pi\frac{k^2}nI}\sum_{j=0}^{n-1}a_je^{\frac {\pi j^2}nI}e^{-\frac{\pi (k-j)^2}nI}$$
设 $B_j=a_je^{\frac {\pi j^2}nI}$
$C_j=e^{-\frac{\pi j^2}nI}$
那么 $$A_k=e^{\pi\frac{k^2}nI}\sum_{j=0}^{n-1}a_jB_jC_{k-j}$$

右边是一个线性卷积，所以我们可以用一次FFT来完成一次DFT

注意，k-j会小于0！
怎么解决这个问题呢？
我们把C右移n位。那么此时
$C_j=e^{-\frac{\pi (j-n)^2}nI}$
由于平方的存在，所以不会有问题。

此时C的长度变为2n。
卷积完之后总长3n。
我们需要考虑哪些部分是有用的。
哪些部分可以保证k-j>=0呢？
即$A_{n..2n-1}$。
那么，最后的答案应该是：$A_k=e^{\pi\frac{k^2}nI}A_{k+n}$
注意IDFT时同样要除以n。

这样我们就完成了项数不变的DFT。实际上，应该叫做CZT。

NTT

数论变换
考虑这个问题：乘起来后系数要模怎么办？

由于单位根是个复数，不能够模。
所以我们要找一个可以代替的东西。

考虑我们用了哪些性质，简单来说，${\omega_n^k}$是一个n阶的循环群。

设我们现在模的质数为$P=2^t\cdot Q+1$
考虑模P意义下的原根g。

由于$g^{0...P-1}$两两不同，$g^P=g$，$g^{2^{t-1}Q}=-1$，所以是一个$2^t\cdot Q$阶的循环群。

进一步，我们可以得到$(g^Q)^{0..P-1}$是$2^t$阶的循环群。
让$n=2^t$即可。

然后我们对应着$\omega_n^k$的定义，定义$G_n^k=g^{\frac {2^tkQ}n}$。
显然$G^k_n$有n个，而且满足$G^k_n=G^{\frac k2}_{\frac n2}$，也满足$G_n^{k+\frac n2}=-G_n^k$

预处理出$g^{kQ}$代替单位根即可。

如果我们要模m，但是m不是$2^tQ+1$形式的质数怎么办？
暴力法：在模m的情况下，每一个系数最大为 m-1，两个乘起来最多$(m-1)^2$，n个加起来最多$n(m-1)^2$。
我们只要凑一个超过$n(m-1)^2$的模数就好了。这样在NTT的过程中，就不会让系数发生变化。然后再去一项一项模。

怎么凑呢？我们用几个小的$2^tQ+1$形式的质数去做NTT，然后用中国剩余定理合并起来就好了。