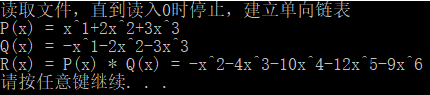一元多项式的乘法与加法运算

article/2025/8/15 9:10:17

题目要求

设计函数分别求两个一元多项式的乘积与和。

输入格式:
输入分2行，每行分别先给出多项式非零项的个数，再以指数递降方式输入一个多项式非零项系数和指数（绝对值均为不超过1000的整数）。数字间以空格分隔。

输出格式:
输出分2行，分别以指数递降方式输出乘积多项式以及和多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。零多项式应输出0 0。

输入样例:

4 3 4 -5 2  6 1  -2 0
3 5 20  -7 4  3 1

输出样例:

15 24 -25 22 30 21 -10 20 -21 8 35 6 -33 5 14 4 -15 3 18 2 -6 1
5 20 -4 4 -5 2 9 1 -2 0

题意分析

在这里插入图片描述
求解思路

多项式表示
程序框架
读多项式
加法实现
乘法实现
多项式输出

多项式表示

数组：编程简单、调试容易；但需要事先确定数组的大小。（可以采用动态数组）
链表：动态性强；编程较为复杂，调试比较困难。（本题用链表表示）

用链表表示：数据域包括系数和指数，指针域指向下一个节点。
在这里插入图片描述

程序框架

main（）函数中包括

读入多相式1
读入多相式2
乘法运算并输出
加法运算并输出
return 0;

因此需要设计的函数有：

读一个多相式
两多项式相乘
两多相式相加
多相式输出

主函数代码用C语言表示如下：

int main()
{Polynomial P1, P2, PP, PS;P1 = ReadPoly();P2 = ReadPoly();PP = Mult(P1, P2);PrintPoly(PP);PS = Add(P1, P2);PrintPoly(PS);return 0;
}

读多项式

ReadPoly（）
读入多相式的基本框架是这样的
在这里插入图片描述
读入之后链表为：

对于每一项，需要将它接到原来的链表之后，就需要再定义一个函数Attach，方便读入多相式。
Rear的初值有两种定义方法：

Rear初值为NULL，在Attach函数中根据Rear是否为NULL做不同处理。
Rear指向一个空结点

这种方法要注意的是最后要释放掉头结点。

Attach（）
在这里插入图片描述

加法实现

在这里插入图片描述
算法思路：
两个指针 P1 和 P2 分别指向这两个多相式的第一个结点，不断循环：

P1->expon = P2->expon : 系数相加，如果结果不等于 0 ，那么作为结果的多项式对应项的系数。同时，P1和P2都指向下一项。
P1->expon > P2->expon : 把P1的当前项存入结果多相式，并使P1指向下一项。
P1->expon < P2->expon : 把P2的当前项存入结果多相式，并使P2指向下一项。

当某一多相式处理完的时候，将另一多项式党的所有结点依次复制到结果多项式。

在这里插入图片描述

乘法实现

方法
在这里插入图片描述

输出多项式

题目中最后的输出每个系数和指数之间是带空格的，而开始没有空格。所以这里设立一个flag，用作输出标记。

void PrintPoly(Polynomial P)
{/* 输出多项式 */int flag = 0; //辅助调整输出格式if (!P){printf("0 0\n");return;}while (P){if (!flag)flag = 1;elseprintf(" ");printf("%d %d", P->coef, P->expon);P = P->link;}printf("\n");
}

完整代码

C语言：

#include <stdio.h>
#include <stdlib.h>struct PolyNode
{int coef;int expon;struct PolyNode* link;
};
typedef struct PolyNode* Polynomial;void Attach(int c, int e, Polynomial* pRear)
{Polynomial P;P = (Polynomial)malloc(sizeof(struct PolyNode));/* 对新结点赋值 */P->coef = c;P->expon = e;P->link = NULL;(*pRear)->link = P;/* 修改pRear值 */*pRear = P;
}Polynomial ReadPoly()
{Polynomial P, Rear, t;int c, e, n;/* 链表头空结点 */P = (Polynomial)malloc(sizeof(struct PolyNode));P->link = NULL;Rear = P;scanf("%d", &n);while (n--){scanf("%d %d", &c, &e);/* 将当前的项插入多相式的尾部 */Attach(c, e, &Rear);}/* 删除临时生成的头结点 */t = P; P = P->link;free(t);return P;
}int Compare(int a, int b)
{if (a > b)return 1;else if (a < b)return -1;elsereturn 0;
}Polynomial Add(Polynomial P1, Polynomial P2)
{Polynomial front, rear, temp;int sum;rear = (Polynomial)malloc(sizeof(struct PolyNode));front = rear; /* front记录结果多项式链表头结点 *//* 当两个多项式都有非零项待处理 */while (P1 && P2){switch (Compare(P1->expon, P2->expon)){case 1:  //P1 指数 更大Attach(P1->coef, P1->expon, &rear);P1 = P1->link;break;case -1: //P2 指数 更大Attach(P2->coef, P2->expon, &rear);P2 = P2->link;break;case 0:  //指数相等sum = P1->coef + P2->coef;if (sum)Attach(sum, P1->expon, &rear);P1 = P1->link;P2 = P2->link;break;}}/* 将未处理完的另一个多项式的所有节点依次复制到结果多项式中去 */while (P1){Attach(P1->coef, P1->expon, &rear);P1 = P1->link;}while (P2){Attach(P2->coef, P2->expon, &rear);P2 = P2->link;}rear->link = NULL;/* 令front指向结果多项式的第一个非零项 */temp = front;front = front->link;free(temp);return front;
}Polynomial Mult(Polynomial P1, Polynomial P2)
{Polynomial P, Rear, t1, t2, t;int c, e;if (!P1 || !P2)return NULL;t1 = P1; t2 = P2;P = (Polynomial)malloc(sizeof(struct PolyNode));P->link = NULL;Rear = P;/* 先用P1的第一项乘以P2，得到P */while (t2){/* 先用P1的第一项乘以P2，得到P2 */Attach(t1->coef * t2->coef, t1->expon + t2->expon, &Rear);t2 = t2->link;}t1 = t1->link;while (t1){t2 = P2; Rear = P;while (t2){e = t1->expon + t2->expon;c = t1->coef * t2->coef;while (Rear->link && Rear->link->expon > e)Rear = Rear->link;if (Rear->link && Rear->link->expon == e){if (Rear->link->coef + c){Rear->link->coef += c;}else {t = Rear->link;Rear->link = t->link;free(t);}}else{t = (Polynomial)malloc(sizeof(struct PolyNode));t->coef = c;t->expon = e;t->link = Rear->link;Rear->link = t;Rear = Rear->link;}t2 = t2->link;}t1 = t1->link;}t2 = P;P = P->link;free(t2);return P;
}void PrintPoly(Polynomial P)
{/* 输出多项式 */int flag = 0; //辅助调整输出格式if (!P){printf("0 0\n");return;}while (P){if (!flag)flag = 1;elseprintf(" ");printf("%d %d", P->coef, P->expon);P = P->link;}printf("\n");
}int main()
{Polynomial P1, P2, PP, PS;P1 = ReadPoly();P2 = ReadPoly();PP = Mult(P1, P2);PrintPoly(PP);PS = Add(P1, P2);PrintPoly(PS);return 0;
}